1.8. Преобразование аналогового сигнала в цифровую форму

1. 8. Преобразование аналогового сигнала в цифровую форму

 

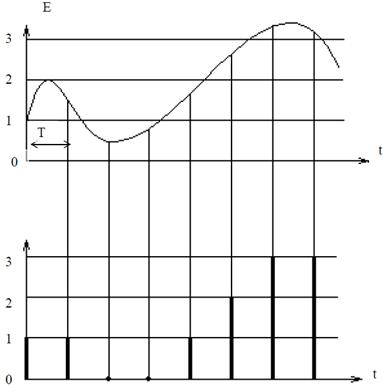
Как указывалось ранее, для перевода сигнала в цифровую форму необходимо осуществить три операции: дискретизацию по аргументу, квантование и кодирование. Первые две операции уже были достаточно подробно рассмотрены выше, в результате их осуществления аналоговый сигнал заменяется суммой дискретных импульсов, амплитуда которых может принимать только разрешенные значения (рис. 1. 17).

 

 

а)
б)

 

Рис. 1. 17. Непрерывный сигнал (а) и дискретный квантованный (б) сигнал Едк

 

Подробнее остановимся на кодировании. Вначале необходимо перевести числа, соответствующие амплитуде отсчетов, в экономичную L-ичную систему счисления. Количество m элементов кодовой комбинации для записи одного числа в z-ичной системе можно определить из условия:

 

m ≥ log_z(N_max +1),

 

где z – разрядность системы, например, для двоичной системы z = 2;

 N_max – максимальное число в десятичной системе из всех чисел, описывающих амплитуду дискретного квантованного сигнала.

Длительность передачи каждого символа должна быть не более T/m, где T – период дискретизации.

Чтобы чрезмерно не увеличивать частоту передачи импульсов, из сообщения необходимо исключить избыточную информацию. Эта избыточная информация подразделяется на три вида: структурная, статистическая, физиологическая [7].

Структурная избыточность возникает при передаче вспомогательной информации, например, сигналов строчной, кадровой и цветовой синхронизации.

 

Статистическая избыточность обусловлена наличием связи между параметрами соседних элементов изображения.

Существование физиологической избыточности вызвано ограниченностью воспринимаемой человеком полосы временных, пространственных, спектральных (в цветовом смысле) частот.

Для уменьшения избыточности производится предварительное преобразование подвергающегося кодированию сигнала.

Преобразование непосредственно самого сигнала в цифровую форму (самый простой случай) называется импульсно-кодовой модуляцией (ИКМ). Наиболее просто сокращение избыточности достигается использованием дифференциальной импульсно-кодовой модуляции (ДИКМ). Здесь в цифровую форму преобразуется не сигнал, а разность между значением сигнала и функцией от ранее переданных отсчетов. Чаще всего эта функция есть сумма произведений переданных отсчетов на коэффициенты весомости [7]. В ДИКМ используется неравномерное квантование. На участках сигнала, где он изменяется медленно (90% сигнала), уровни квантования расположены " густо", а для больших скачков сигнала используется " редкое" квантование. В результате для передачи одного отсчета можно использовать вдвое меньше разрядов, чем при ИКМ с постоянным шагом квантования.

Более эффективно, хотя и более сложно, избыточность сокращается при кодировании с преобразованием (блочном). Здесь кодированию подлежат не значения квантованного сигнала, а коэффициенты некоторого его преобразования, например Фурье.

Пространственный спектр большей части сигналов, в основном состоит из низкочастотных составляющих, убывает с ростом частоты. Поэтому для передачи информации о спектральных составляющих можно использовать меньшее число отсчетов и квантовать их более грубо, чем в ИКМ. Количество разрядов для передачи одного элемента ТВ-изображения при двоичном кодировании в этом случае сокращается с 8 до 2–2, 5.

Если кодировать адаптивно, т. е. выбирать функцию преобразования в зависимости от сигнала, цифровой поток можно сжать до 0, 1–0, 2 бит на элемент [7].

Если на первой стадии кодирования осуществить косинусное преобразование, на второй использовать адаптивную ДИКМ (такой способ кодирования называется гибридным ), то сжатие составляет 0, 5–0, 25 бит на элемент.

Вышеприведенная информация о методах кодирования содержит лишь основы, необходимые для составления понятия о преобразовании сигнала в цифровую форму, и способствует изучению этого вопроса достаточно глубоко.

1. 9. Амплитудная и угловая модуляция сигнала

 

При передаче низкочастотных медико-биологических сигналов возникают следующие проблемы: сложная техническая реализация усиления, невозможность непосредственной передачи по радиоканалу (при телеметрии). Для их решения применяют модуляцию, то есть наложение низкочастотного исходного сигнала на высокочастотное гармоническое колебание (несущую).

Амплитудная модуляция (АМ) есть наиболее простой и распространенный вид модуляции. При АМ огибающая амплитуда изменяется по закону изменения передаваемого сообщения, частота и начальная фаза несущей остается неизменной:

 

,

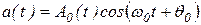(1. 58)

 

где a(t) – высокочастотный (ВЧ) сигнал с модулированной амплитудой a₀(t);

 A₀(t) – амплитуда огибающей, определяемая видом передаваемого сообщения E(t);

 w₀ – частота высокочастотного колебания;

 q₀ – начальная фаза высокочастотного колебания.

Огибающая непрерывного сигнала a(t) изменяется по закону, воспроизводящему исходное сообщение E(t), приведенное на рис. 1. 18, а, а модулированный сигнал a(t) показан на рис. 1. 18, б.

 

 

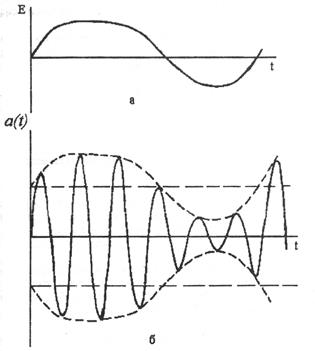
Рис. 1. 18. Исходное сообщение (а) и модулированный по амплитуде сигнал (б)

 

Основным параметром АМ-колебания является глубина модуляции. Определение этого понятия особенно наглядно для однотональной модуляции, когда модулирующая функция (исходное сообщение E(t)) является гармоническим колебанием:

 

,

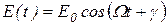(1. 59)

 

где W – угловая частота модулирующего сигнала;

g – начальная фаза модулирующего сигнала.

Огибающую модулированного колебания при этом можно представить в виде

 

,

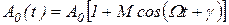(1. 60)

 

где A₀ – амплитуда несущей в отсутствие модуляции;

 М – коэффициент амплитудной модуляции, определяемый по формуле:

 

,

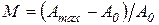(1. 61)

 

где А_max – максимальная амплитуда модулированного колебания.

При неискаженной модуляции (M ≤ 1) амплитуда колебания изменяется в пределах от минимальной A_min = A₀(1 – M) до максимальной A_min = A₀(1 + M).

Из (1. 58) и (1. 60) следует:

 

.

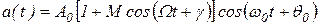(1. 62)

 

Используя тригонометрическую формулу произведения косинусов, из (1. 62) получаем выражение для однотонального АМ-сигнала в виде:

 

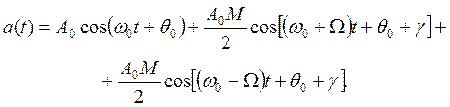
(1. 63)

 

Из (1. 63) видно, что спектр S(n) однотонального АМ-сигнала (рис. 1. 19) имеет три составляющих: w₀ – несущая частота; w₀ + W – верхняя боковая частота; w₀ – W – нижняя боковая частота.

 

 

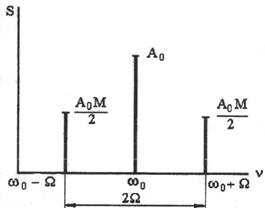
Рис. 1. 19. Спектр однотонального АМ-сигнала

 

На практике однотональные АМ-сигналы используются редко, т. к. более реален случай, когда модулирующий сигнал имеет сложный спектральный состав, и его можно представить в виде суммы гармоник:

 

,

(1. 64)

 

где E_0i – амплитуда i-й гармоники;

 W_i – ее частота;

 g_i – ее начальная фаза;

 N – число гармоник.

Введем совокупность парциальных (частичных) коэффициентов модуляции M_i:

 

Mi = ME0i,

(1. 65)

 

запишем выражение для многотонального АМ-сигнала:

 

.

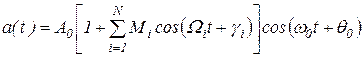(1. 66)

 

Спектральный состав сигнала выражается формулой:

 

.

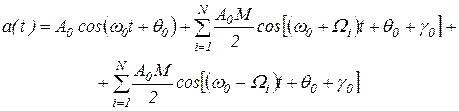(1. 67)

График АЧХ многотонального АМ-сигнала представлен на рис. 1. 20.

 

 

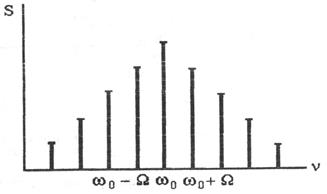
Рис. 1. 20. График АЧХ многотонального АМ-сигнала

 

Модулированный сигнал может получаться также за счет того, что в несущем гармоническом колебании  E(t) изменяет либо частоту w₀, либо начальную фазу q₀ при неизменной амплитуде.

Поскольку аргумент гармонического колебания 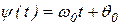, называемый полной фазой, определяет текущее значение фазового угла, такая модуляция называется угловой.

Если полная фаза y(t) связана с сигналом E(t) зависимостью 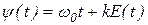, где k – некоторый коэффициент пропорциональности, то такая модуляция называется фазовой (ФМ).

Модулированный сигнал A_фм(t) описывается уравнением:

 

.

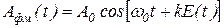(1. 68)

 

График ФМ-сигнала показан на рис. 1. 21. Предельное значение фазового сдвига называют девиацией фазы D_y.

 

 

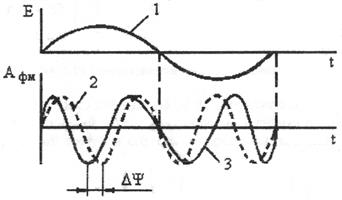
Рис. 1. 21. График ФМ-сигнала:

1 – исходное сообщение; 2 – несущая при отсутствии модуляции; 3 – модулированный сигнал

 

Мгновенная частота w(t) сигнала с угловой модуляцией определяется как первая производная от полной фазы по времени:

 

.

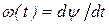(1. 69)

 

При частотной модуляции (ЧМ) между величинами E(t) и w(t) имеется связь вида 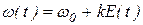, поэтому частотно-модулированный сигнал A_чм(t) имеет вид:

 

.

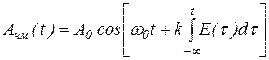(1. 70)

 

Начальная фаза q₀ здесь для упрощения принята равной нулю.

Естественным параметром ЧМ-сигнала является девиация частоты Dw.

В случае однотонального ЧМ-сигнала мгновенная частота

 

,

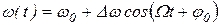(1. 71)

 

полная фаза сигнала

 

.

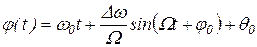(1. 72)

 

Величина m = Dw/W называется индексом однотональной угловой модуляции и представляет собой амплитуду изменения фазы сигнала.

Положим, что постоянные фазовые углы j₀ = q₀ = 0. Тогда ЧМ-сигнал E_чм можно представить в виде:

 

.

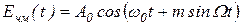(1. 73)

 

Формула для ФМ-сигнала аналогична.

Спектральная полоса частот, занимаемая однотональным сигналом с угловой модуляцией, расширяется с ростом индекса модуляции и выражается через функции Бесселя. Для простоты на практике частотную границу АЧХ П определяют по формуле:

 

П = 2(m + 1)W.

(1. 74)

 

Многотональный модулирующий сигнал раскладывают в ряд Фурье по частотам W₁, W₂,..., W_n.

Тогда A_чм-сигнал можно представить в виде

 

,

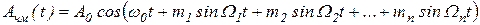(1. 75)

 

где m₁, m₂, ..., m_n – индексы угловой модуляции для каждой тональной составляющей.

АЧХ такого сигнала занимает полосу частот от 0 до П:

 

П = 2(mn + 1)Wn.

(1. 76)

 

Операция демодуляции АМ-сигнала противоположна амплитудной модуляции. Имея на входе идеального демодулятора АМ-колебание 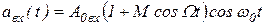, следует получить на выходе низкочастотный сигнал 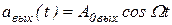, пропорциональный передаваемому сообщению. Эффективность работы демодулятора принято оценивать коэффициентом демодуляции

 

,

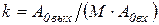(1. 77)

 

равным отношению амплитуды низкочастотного сигнала на выходе к размаху изменения амплитуды высокочастотного сигнала на входе. Можно осуществить детектирование, подав АМ-сигнал на безынерционный нелинейный элемент и предусмотрев последующую фильтрацию низкочастотных составляющих спектра.

Демодуляция ФМ-сигнала основана на нелинейном взаимодействии модулированного сигнала с немодулированным опорным колебанием A_оп(t) той же частоты, которое должно создаваться вспомогательным внешним источником. Сравнение фазы модулированного сигнала и опорного колебания может осуществляться с использованием перемножения колебаний A_фм(t) и A_оп(t). На выходе перемножителя получаем:

 

,

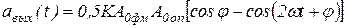(1. 78)

 

где A_0фм – амплитуда модулированного сигнала;

 A_0оп – амплитуда опорного сигнала;

 K – коэффициент перемножителя.

 

 

После фильтрации сигнала a_вых(t) с помощью фильтра нижних частот получаем:

 

.

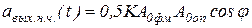(1. 79)

 

Демодуляция ЧМ-сигнала может осуществляться на основе преобразования изменения частоты в изменение амплитуды с последующей амплитудной демодуляцией. Преобразование ЧМ-сигнала в АМ-сигнал выполняется с помощью устройства, АЧХ которого имеет линейно нарастающий участок вблизи центральной частоты ЧМ-сигнала, например с помощью линейного частотного фильтра, настроенного таким образом, чтобы в разложении АЧХ коэффициент 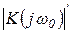 был отличен от нуля:

 

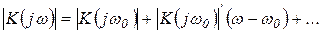
(1. 80)

 

Тогда, полагая, что частота модулированного сигнала 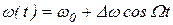, получим на выходе фильтра сигнал со сложной амплитудно-угловой модуляцией. Мгновенная амплитуда переменной составляющей этого сигнала изменяется во времени по закону

 

,

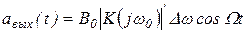(1. 81)

 

где B₀ – постоянный коэффициент, т. е. повторяет по форме передаваемое сообщение.

Окончательная обработка сигнала производится обычным АМ-демодулятором, включенным на выходе фильтра.

В телеуправлении и телеизмерении (телеметрии) кроме непрерывных видов модуляции, рассмотренных выше, также используют импульсную модуляцию. В этом случае несущая (или поднесущая, если имеется несколько каналов передачи информации) представляет собой последовательность прямоугольных импульсов. Различают амплитудно-импульсную (АИМ), широтно-импульсную (ШИМ), частотно-импульсную (ЧИМ), фазово-импульсную (ФИМ) и кодово-импульсную (КИМ) модуляцию. Полезный сигнал заменяется отсчетами в моменты Т, 2Т, 3Т и так далее.

В случае АИМ амплитуда каждого импульса модулированного сигнала зависит от мгновенного значения амплитуды полезного сигнала, как показано на рис. 1. 22.

 

 

Рис. 1. 22. Форма сигналов при АИМ:

а – форма модулированного сигнала; б – воспроизведенная форма сигнала при низкой частоте следования импульсов, Т₁ – период следования импульсов; в – воспроизведенная форма сигнала при высокой частоте следования импульсов, Т₂ – период следования импульсов

 

Этот процесс может быть выполнен путем выборки аналогового сигнала через постоянные интервалы времени импульсами выборки с фиксированной длительностью. Импульсы выборки – это импульсы, амплитуды которых равны уровню первоначального аналогового сигнала в момент выборки. Как видно из рисунка, при высокой частоте импульсов несущей восстановленный сигнал имеет большее сходство с исходным аналоговым сигналом, чем при низкой. Частота выборки (число импульсов в секунду) должна быть, по край­ней мере, в два раза большей, чем самая высокая частота аналогового сигнала. Для лучшей воспроизводимости частота выборки обычно устанавливается в 5 раз большей самой высокой частоты модуляции. Амплитуда АИМ-сигнала описывается уравнением:

 

,

 

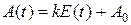где k – глубина модуляции;

 А₀ – амплитуда импульсов несущей.

В случае ШИМ амплитуда и период импульсов несущей неизменны, длительность каждого импульса пропорциональна амплитуде полезного сигнала в момент начала импульса (рис. 1. 23).

 

 

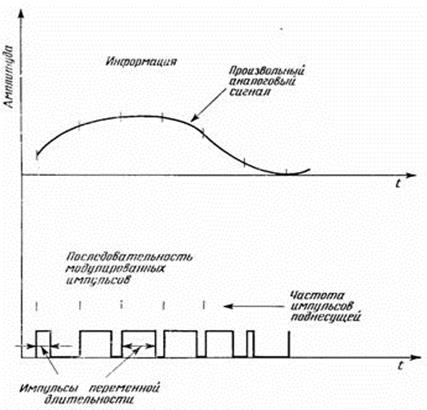
Рис. 1. 23. Широтно-импульсная модуляция

 

Длительность импульса ШИМ-сигнала определяется уравнением:

 

,

 

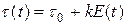где t₀ – длительность импульса в отсутствие модуляции.

В случае ЧИМ или ФИМ амплитуда и длительность импульсов несущей неизменны, частота или фаза меняются в зависимости от амплитуды полезного сигнала в момент отсчета, то есть импульсы сдвигаются по временной оси. Поэтому ЧИМ и ФИМ относят к времяимпульсной модуляции (ВИМ).

Сдвиг фазы импульса при ФИМ: 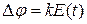; период следования импульсов при ЧИМ: 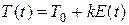, где Т₀ – период следования импульсов в отсутствие модуляции.

При КИМ каждый отсчет полезного сигнала преобразуется в последовательность импульсов, квантованных по уровню в соответствии с каким-либо кодом (рис. 1. 24).

 

 

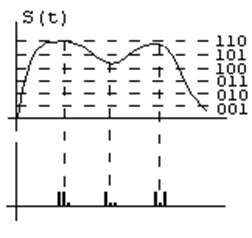
Рис. 1. 24. Кодово-импульсная модуляция

 

Вместо полезного сигнала передается набор чисел, каждое из которых соответствует уровню полезного сигнала в момент отсчета. Примером КИМ может служить аналого-цифровое преобразование.

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: