 |
2.2. Спектральные характеристики случайных сигналов
|
|
|
|
2. 2. Спектральные характеристики случайных сигналов
Для случайных сигналов в частотной области принято рассматривать не амплитудные, а энергетические характеристики, т. к. из-за случайности и независимости фаз спектральных составляющих в различных реализациях усреднение спектральной плотности дает нулевой спектр переменной составляющей сигнала[1].
По реализации процесса x(t) или ее спектральной плотности S(τ ) можно найти энергию Э этой реализации:
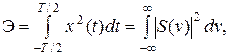
| (2. 17) |
где T – длина реализации.
Средняя мощность реализации Nср есть
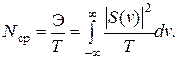
| (2. 18) |
При анализе эргодических процессов длина реализации стремится к бесконечности, в этом случае формула для расчета средней мощности реализации имеет вид
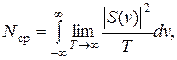
| (2. 19) |
где зависящий от частоты v предел есть спектральная плотность n(v) средней мощности:
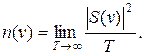
| (2. 20) |
Спектральная плотность средней мощности представляет собой зависимость средней мощности, приходящейся на единицу частоты, от частоты.
Формула (2. 20) используется, если постоянная составляющая сигнала равна нулю. В случае наличия постоянной составляющей спектральная плотность есть сумма двух слагаемых:
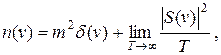
| (2. 21) |
где m – математическое ожидание;
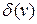– дельта-функция Дирака.
Интеграл первого слагаемого в формуле (2. 21) есть мощность постоянной составляющей, а интеграл левого слагаемого – мощность флуктуационной составляющей (дисперсия).
В соответствии с теоремой Винера-Хинчина спектральная плотность средней мощности n(v) и ковариационная функция Kx(t) связаны между собой преобразованиями Фурье:
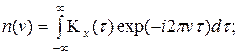
| (2. 22) | |
| (2. 23) |
Соответственно для процессов с равной нулю постоянной составляющей преобразованием Фурье связаны корреляционная функция Rx(τ ) и спектральная плотность средней мощности n(v):
|
|
|
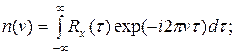
| (2. 24) | |
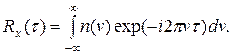
| (2. 25) |
При прохождении случайного стационарного сигнала через линейный фильтр с АЧХ K(v) спектральная плотность на выходе nвых(v) связана с входной спектральной плотностью nвх(v) соотношением:
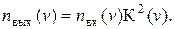
| (2. 26) |
Произведение частотных характеристик соответствует свертке корреляционных функций:
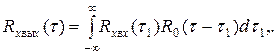
| (2. 27) |
где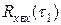 
и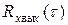 
– корреляционные функции на входе и выходе фильтра; 
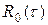– корреляционная функция импульсной реакции фильтра E0(t); τ и τ 1 – аргументы сигнала на входе и выходе фильтра.
2. 3. Шумы при передаче информации
Системы приема, преобразования, воспроизведения информации, кроме того, что обрабатывают анализируемый сигнал, воспринимают и сами генерируют изменения физических величин, не несущих информацию. Такие изменения физических величин называют шумами или помехами. Уровень шумов определяет как точность воспроизведения, так и скорость передачи информации. Так как шум представляет собой случайный процесс, то для его оценки используют те же статистические характеристики.
По характеру взаимодействия с сигналом и между собой шумы чаще всего подразделяются на аддитивные (результат взаимодействия – сумма), мультипликативные (результат взаимодействия – произведение), возможны также и результаты других комбинаций.
Рассмотрим источники шумов. Разделение шумов на три группы произведено на основе предложенной в [11] классификации. Первая группа включает шумы, генерируемые объектом исследования, вторая – внешние воздействия, третья – шумы аппаратуры и носителей информации.
Шумы объекта возникают, во-первых, при наложении на исследуемый сигнал других сигналов той же природы (например, электромиограмма на кардиосигнал), во-вторых, от движений объекта и его частей.
|
|
|
Внешние шумы могут быть обусловлены природными и искусственными факторами. Первые включают в себя флуктуации природных фоновых полей и излучений, других явлений. К последним можно отнести синфазные флуктуационные и импульсные помехи от электромагнитных полей силовой сети и других источников полей, акустический шум, вибрации.
Шумы аппаратуры обусловлены, главным образом, природой физических явлений, происходящих в элементах электрических схем. В основном это тепловой, дробовый, генерационно-рекомбинационный, токовый шумы.
Тепловой шум вызван возникновением переменной ЭДС на концах сопротивления, обусловленной тепловым хаотическим движением носителя заряда. Спектральная плотность этого шума зависит от значений сопротивления и его температуры.
Дробовый шум (шум Шоттки) возникает за счет дискретности частиц, образующих электрический ток в электронной лампе. Эммитация электронов катодом и достижение ими анода – случайные процессы. В многоэлектродных лампах случайный характер распределения тока между сетками вызывают шум токораспределения.
Генерационно-рекомбинационный шум аналогичен дробовым шумам в вакуумных приборах и является основным для полупроводников на промежуточных частотах. Его наличие обусловлено случайным характером процессов генерации и рекомбинации носителей зарядов. Значения спектральной плотности зависят от времени жизни, концентрации и подвижности носителей заряда.
Токовый шум преобладает в полупроводниках на низких частотах (модуляционный), существует также в графитовых сопротивлениях, электрических контактах (контактный) и в вакуумных лампах (шум мерцания или фликкер-эффект). Экспериментально установлено, что спектральная плотность такого шума обратно пропорциональна частоте со степенным показателем 0, 8–1, 5 [12].
При недостаточно жестком креплении элементов схемы и вибрациях электроаппаратуры может возникать микрофонный шум. В результате вибраций электродов монтажных проводов и корпуса происходит изменение межэлектродных и монтажных емкостей и сопротивление полупроводника, используемого как приемник излучения. Микрофонный шум состоит из ряда резонансных выбросов в диапазоне 100–7000 Гц [12].
|
|
|
В аппаратуре, связанной с оптическим излучением, необходимо принимать во внимание и фотонный (радиационный) шум, обусловленный флуктуациями потока излучения, падающего на приемник за счет флуктуаций числа фотонов, эммитируемых источником излучения.
Температурный шум наблюдается только в тепловых приемниках из-за флуктуаций температуры приемника при обмене с окружающей средой и зависит от температуры приемника, окружающей среды.
Более подробная информация о вышеперечисленных видах шума в аппаратуре и расчетные формулы приведены в [12, 13].
К источникам шума при записи сигналов относятся и носители информации (светочувствительные, магнитные и др. ) за счет случайного распределения " запоминающих" элементов в носителе.
Фотографическое почернение равномерно засвеченного и проявленного светоматериала есть двумерное случайное поле, обладающее изотропностью, стационарностью и эргодичностью [14]. Спектр фотографических шумов называют спектром гранулярности фотоматериалов. Интенсивность этого спектра зависит как от свойств фотоматериала (светочувствительность), так и режимов его обработки. Более подробная информация о гранулярности фотоматериалов приведена в [14].
Аналогично параметры шума магнитных носителей записи определяются свойствами намагничиваемых частиц и характером их распределения на носителе.
В [12] влияние шума на качество передачи сигнала предлагается оценивать отношением Δ φ ( сигнал/шум ), вычисляемым по формуле
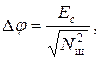
| (2. 28) |
где Eс – энергия изображения;
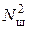– квадрат шумовой составляющей.
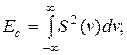
| (2. 29) | |
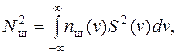
| (2. 30) |
где S(v) – АЧХ сигнала;
nш(v) – спектральная плотность средней мощности шума.
Если зашумленный сигнал проходит через фильтр с АЧХ K(v), то формулы (2. 9) и (2. 30) принимают вид:
| (2. 31) | |
 .
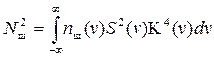| (2. 32) |
Существуют и другие подходы к вычислению отношения " сигнал/шум". Например, это отношение W(v) для светочувствительных материалов рассчитывается по формуле в [14]:
|
|
|
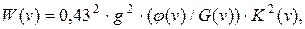
| (2. 33) |
где 0, 43 – коэффициент перевода оптической плотности в коэффициент пропускания;
g – коэффициент контрастности (максимальный градиент характеристической кривой);
φ (v) – спектральная плотность средней мощности сигнала;
G(v) – спектр гранулярности фотоматериала;
K(v) – АЧХ фотоматериала.
Очевидно, что при расчете по формуле (2. 33) отношение " сигнал/шум" является функцией частоты.
Важнейшей проблемой при обработке сигналов является борьба с шумами. Одним из способов ослабления отрицательного воздействия шумов является выбор оптимального фильтра. Критерии оптимальности зависят от поставленной задачи: обнаружение сигналов, измерение его параметров или разрешение (различение) сигналов.
Для первой задачи (обнаружение сигнала в шуме) критерием является максимум отношения " сигнал/шум", а оптимальный фильтр имеет комплексную частотную характеристику, сопряженную со спектральной плотностью сигнала [1].
В [11] предлагаются следующие методы фильтрации шумов, позволяющие производить оценку сигнала: полосовой, нелинейный, компенсационный. Полосовой метод предусматривает фильтрацию шумов, частотный диапазон которых не совпадает с частотным диапазоном сигнала. При нелинейной фильтрации производится частотно-независимое сглаживание шумов, попадающих в полосу пропускания сигнала, за счет использования следящей системы направленного действия и гистерезисного компаратора с адаптацией по уровню шума. Компенсационная фильтрация устраняет наводки от сети с помощью двухкоординатной следящей системы по частоте и фазе наводки.
Критериями при визуализации изображений в медицинской технике являются постоянство нормы вектора шума либо максимум энтропии. Подобная информация и математический аппарат для двух последних критериев содержатся в [15].
Вышеуказанные способы борьбы с шумом посредством оптимальной фильтрации являются далеко не единственными. Для решения этой задачи может использоваться перевод сигнала в цифровую форму и многое другое.
|
|
|
