1.10. Критерии резкости

Критерии резкости изображения в основном можно разделить на две большие группы: использующие параметры функции рассеяния края (ФРК) и использующие параметры амплитудно-частотной характеристики (АЧХ). ФРК – это распределение освещенности в изображении края светящейся полуплоскости. Входной сигнал «светящееся полуплоскость» математически описывается функцией Хэвисайда: для отрицательных значений аргумента эта функция равна 0, для положительных значений она равна 1. АЧХ есть зависимость коэффициента передачи контраста от частоты.

В качестве критериев, использующих ФРК, предлагалось приме­нять среднеквадратичный градиент ФРК, произведение его и мак­симальной разности оптических плотностей в изображении края, другие модификации. В результате исследований было установлено, что указанная группа критериев не дает однозначной связи с субъективной оценкой резкости.

Критерии, использующие АЧХ, в свою очередь, можно классифицировать по трем группам: а) критерии использующие координаты АЧХ - разрешающую способность и критическую частоту (абсцисса точки АЧХ, ордината которой равна е^-1), б) использующие площадь под АЧХ и ее математические преобразования, в) информационные критерии. Критерии первой группы пригодны для сравнительной оценки систем, имеющих АЧХ подобной формы, так как учитывают координаты только одной точки АЧХ. Вторая группа критериев позволяет более полно оценить воспроизводящие свойства систем, так как учитывается характер АЧХ в целом, но вследствие отсутствия физического обоснования выбора критериев отсутствует их однозначная связь с визуальной оценкой резкости.

В настоящее время получили широкое распространение информа­ционные критерии. Информационные  параметры универсальны, т. к. применимы к информации любого вида и содержания. Информацион­ный подход к оценке качества находится в соответствии с положением о том, что система тем лучше воспроизводит изображение объекта, чем большее количество информации о нем она передает.

В. Г. Комар информационную емкость системы определяет как логарифм максимального количества изображений, в том числе и лишенных смыслового содержания, которое может воспроизвести система, если появление любого изображения равновероятно. С. М. Проворнов и О. Ф. Гребенников в качестве информационного критерия рассматривают максимальную энтропию Н, равную количеству информации, которую можно получить о некоторой системе:

 

 

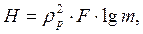
где 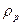 – разрешающая способность,

F – площадь кадра,

m – число градаций яркости, различимых в каждой точке.

Эксперименты Н. Н. Красильникова и других показали, что изображения, состоящие из дискретных пространственных элементов, принимающих дискретные значения яркости, оцениваются как имеющие одинаковое качество, если содержащееся в них количество информации Н, рассчитанное по вышеуказанной формуле, одинаково, С. М. Проворновым и О. Ф. Гребенниковым отмечено, что критерий " количество информации" в предложенной ими форме не учитывает для непрерывных в пространстве изображении корреляцию яркостей соседних участков изображения, вызванную тем, что, вследствие неидеальной передачи системой, изображения соседних точек перекрывают друг друга. Чтобы уменьшить влияние взаимного перекрытия изображений соседних точек, вызванного неидеальной передачей, В. Г. Комар предлагает располагать точки отсчета на более далеком расстоянии, обратном не разрешающей способности 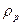, в критической частоте f_e, т. е.

 

 

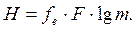
С использованием указанной формулы В. Г. Комар и Е. М. Голдовский произвели сравнительный анализ различных систем по величине информационной емкости.

Однако результаты такого анализа являются приближенными по следующим причинам, Во-первых, учет корреляции яркостей соседних точек с использованием в расчетной формуле критической частоты вместо разрешающей способности есть допущение, погрешность которого не была оценена. Кроме того, остался нерешенным вопрос о величинах субъективных оценок резкости и четкости, соответствующих подученным значениям информационной емкости. Рассмотренные информационные критерии позволяют лишь приближенно оценить количество информации, передаваемое системой.

О. Ф. Гребенников при сопоставлении определения информационной емкости В. Г. Комара и понятия энтропии из теории информации показал: информационная емкость дискретной системы численно равна максимальной энтропии ансамбля дискретных сообщений. Отсюда был сделан вывод, что при рассматривании системы как линейного фильтра для расчета ее информационной емкости возможно применить теорему К. Шеннона о потере энтропии в фильтре. Представление системы в качестве линейного фильтра является условным, так как она может содержать и нелинейные звенья, например, фотографические материалы. Однако, как било показано Р. Ламбертсом, АЧХ двух – и четырехступенчатого процесса печати с одного светочувствительного материала на другой с большой степенью точности определяется произведением АЧХ звеньев каждой ступени, поэтому принятое допущение о линейности системы в первом приближении можно считать достаточно правомерным.

Эксперименты О. Ф. Гребенникова и А. К. Кулакова дают основание считать, что значения информационной плотности, приведенной к поверхности сетчатки и рассчитанной с учетом потери энтропии в системе, хорошо согласуются с субъективной оценкой резкости и четкости киноизображений. Но предложенный подход является также в известной мере приближенным. Во-первых, сделано допущение о дискретности воспроизводимых системой градаций яркости, Фактически возможные значения яркости в любой точке

изображения представляют непрерывное множество. Во-вторых, потеря энтропии рассчитывается для случая, когда система рассматривается как одномерная, а функция передачи модуляции реальной кинематографический системы фактически является двумерной и в подавляющем большинстве случаев анизотропной.

Анизотропия АЧХ системы может быть вызвана различными причинами. В частности, такую АЧХ имеют анаморфотные оптические системы, которые увеличивают различно ориентированные в пространстве объекты по-разному. Кроме того, к анизотропии АЧХ приводят процессы вибраций и сдвигов оптического изображения относительно носителя при записи и воспроизведении информации, если направление этих сдвигов и вибраций перпендикулярно оптической оси.

Из-за наличия в системах рассмотренных выше видов сдвигов и наличия звеньев с анизотропной АЧХ, двумерная АЧХ системы в целом, определяемая как произведение. АЧХ составляющих звеньев, также представляет собой анизотропную характеристику, т. е. форма АЧХ зависит от двух частотных пространственных координат.

Для таких двумерных фильтров и систем, известна теорема о потере энтропии, приведенная у Р. Реллера.

Формула Р. Реллера для вычисления потери энтропии на степень свободы Q в линейном двумерном фильтре в померных координатах имеет вид:

 

 

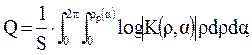
где α – полярный угол;

ρ – пространственная частота в направлении, соответствующем полярному углу α;

ρ p(α ) – значение пространственной частоты ρ на границе области, внутри которой рассматривается АЧХ или разрешающая способность в направлении, соответствующем полярному углу α;

K(ρ, α ) – АЧХ фильтра;

S – площадь частотной области, в пределах которой рассматривается АЧХ (где K(ρ, α ) ≥ Т пред);

Тпред – минимальное возможное значение коэффициента передачи модуляции системы (фильтра), определяемое шумами в системе.

Площадь частотной области S можно найти в полярных координатах следующим образом:

 

Q

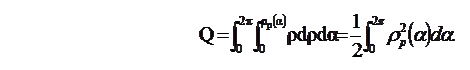
(1. 82)

 

Для вычисления энтропии на выходе фильтра (системы) необходимо найти, кроме потери энтропии, еще число степеней свободы (точек отсчета) при условной дискретизации киноизображения и энтропию сообщения, приходящуюся на степень свободы на входе системы.

Изображение в любой системе имеет конечные размеры, т. е. можно рассматривать как сигнал с ограниченной протяженностью. Для таких сигналов справедлива теорема отсчетов в частотной области, приведенная С. Голдманом для одномерного случая, согласно которой спектр K(f) сигнала протяженностью D однозначно определяется последовательностью дискретных значений в точках, отстоящих на расстояние 1/D.

К применению указанной теоремы в многомерном пространстве известны два подхода, первый из которых заключается в следующем: n-мерное пространство расчленяется на n взаимно перпендикулярных одномерных пространств, и затем теорема применяется к каждому из этих пространств. Согласно второму подходу, число точек отсчета определяется функцией отсчетов, выбираемой таким образом, чтобы эффективность дискретизации, обратно пропорциональная минимально необходимому числу отсчетов на единицу объема, была максимальной для всех возможных способов дискретизации.

Так как изображение в большинстве систем представляет собой прямоугольник высотой h_k и  шириной b_k, то рациональней использовать первый подход, который, в данном случае, находится в соответствии со вторым (ортогональная дискретизации здесь обеспечивает и максимальную эффективность).

Из вышеизложенного вытекает возможность ортогональной дискретизации АЧХ, причем шаг дискретизации по вертикали равен I/h_k, а по горизонтали I/b_k.

Тогда число степеней свободы (точек отсчета) p найдем следующим образом:

 

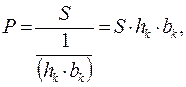
(1. 83)

 

где S – площадь частотной области, в которой рассматривается АЧХ;

 h_k – высота изображения;

 b_k – его ширина.

Найдем энтропию изображения в каждой точке отсчета (приходящуюся на степень свободы).

Если фильтр идеальный, то в нем отсутствует  потеря энтропии и входная энтропия равна энтропии на выходе фильтра. (Под идеальным будем понимать такой фильтр, АЧХ которого во всей рассматриваемой частотной области равна I и ограничивающее действие которого обусловлено только шумом в нем). Тогда максимальная входная энтропия на степень свободы равна максимальному количеству состояний, которые можно передать идеальным фильтром в каждой точке отсчета. Число интервалов m между уровнями, различимыми после передачи спектральной составляющей S^’ идеальным фильтром, равно:

 

m = S’/Δ S’,

(1. 84)

 

где Δ S^’ – величина интервала между различимыми уровнями, обусловленная шумом в фильтре, равная 0, 024 (минимальное значение коэффициента передачи Тпред, которое может передать кинематографическая система).

Значения спектральной составляющей S, передаваемые в каждой точке отсчета, представляют собой непрерывное множество.

Для непрерывных величин x С. Голдман  предлагает находить энтропию Нp ансамбля сообщений по формуле:

 

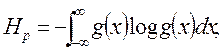
(1. 85)

 

где g(x) – плотность вероятности распределения непрерывной величины x.

Так как в рассматриваемом случае непрерывной величиной x является спектральная составляющая S', принимающая значения от О до S’_mas равного I, то из

 

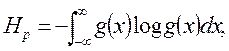
получим

 

 

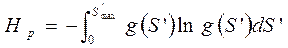
или, приняв во внимание, что m=S^’/Δ S^’, получаем:

 

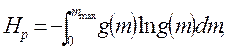
(1. 86)

 

где g(m) – плотность вероятности различения интервалов между уровнями;

 m_max – максимальное число интервалов между уровнями, которые можно различать в данной точке отсчета, причем

 

m_max = S^’_max/T_пред = 1/T_пред.

 

Так как согласно определению информационной емкости появление любого изображения, а значит, и любого уровня, равновероятно, то плотность вероятности g (S') и, следовательно, g(m) распределены равномерно, т. е. с учетом нормирования плотности вероятности имеем

 

.

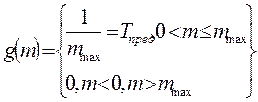(1. 87)

 

Подстановка (1. 86) в (1. 85) дает:

 

H_p = ln(1/T_пред).

 

Энтропию Н’ сообщения (изображения, на выходе системы, а, следовательно, в информационную емкость кинематографической системы можно вычислить по формуле):

 

Н’ = p(Нp + Q),

(1. 88)

 

где р – число степеней свободы;

H_p – энтропия, приходящаяся на степень свободы, на входе системы;

Q – потеря энтропии на степень свободы.

Подстановка (1. 82), (1. 83) и (1. 87) в (1. 88) дает формулу для расчета энтропии на выходе H’, а следовательно, и информационной емкости:

 

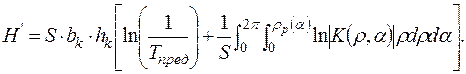
(1. 89)

 

Анализ формулы (1. 89) показывает, что информационная емкость зависит как от площади изображения, так и от параметров АЧХ. Поэтому в дальнейших исследованиях целесообразно использовать также понятие информационной плотности h, определяемой информационной емкостью на единицу площади изображения и зависящей только от параметров АЧХ:

 

h = H’/(bkhk),

(1. 90)

 

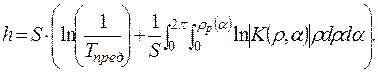
(1. 91)

 

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: