3.3. Количественная оценка цветовоспроизведения

Известны два способа количественного описания цветности изображений: первый – по цветовому тону и чистоте цвета, второй – по цветовым координатам.

Так как любой цвет можно представить как сумму монохроматического и белого, то цветовой тон характеризуется длиной волны λ этого монохроматического излучения. Исключение составляет пурпурный цвет. Его тон характеризуется длиной волны дополнительного цвета, который дает в смеси с пурпурным белый цвет.

Чистотой цвета Р называется отношение яркости В монохроматической составляющей к сумме яркостей этой монохроматической составляющей и белого цвета Вσ:

Для пурпурных цветов в формулу (3. 1) вместо В подставляют яркость " чистого" пурпурного света В_n.

Если использовать полярные координаты, то тон соответствует полярному углу, а чистота цвета – длине радиус-вектора, причем нулевая точка соответствует белому цвету, единичная длина вектора – монохроматическому излучению.

Более распространенным и удобным с точки зрения преобразований способом количественной оценки цвета является система цветовых координат. Основой системы являются три основных линейно-независимых цвета. Таких триад может быть множество, но на практике используются три системы: RGB, XYZ, UVW.

Первой возникла система RGB. Она единственная, где используются физически воспроизводимые монохроматические излучения с длинами волн 700 нм (красный цвет R), 546, 1 нм (зеленый G) и 435, 8 нм (синий B). Система неудобна тем, что для синтеза некоторых цветов вместо сложения RGB приходится производить вычитание одного из трех основных цветов.

Более совершенной системой является система XYZ, где используются нереальные цвета. В этой системе вся яркость синтезируемого цвета условно отнесена к основному цвету Y, а цвета X и Z яркостями не обладают.

Цвет, выраженный численно без учета яркости, называют цветностью, а числа, определяющие цветность – координатами цветности. Координаты цвета X, Y, Z (с учетом яркости) и координаты цветности X', Y', Z' связаны между собой соотношениями:

Очевидно, что X' + Y' + Z' = 1, поэтому для задания цветности (без яркости) достаточно двух координат.

Для указания количества основных цветов в смеси, т. е. определения цветовых координат, используется понятие единичного цвета. За единичные цвета принимаются такие количества (например, в яркостном выражении) основных цветов, которые дают белый цвет равноэнергетического излучения.

Удельные координаты x, y, z (они же кривые смешения) показывают, в каких количествах надо смешивать основные цвета, чтобы получить требуемое монохроматическое излучение с единичной лучистой яркостью. Координаты цвета X, Y, Z источника излучения связаны с удельными координатами x, y, z в функции λ (кривыми смешения в системе XYZ) и спектральным составом источника излучения B(λ ) следующими соотношениями:

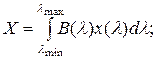
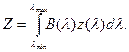
(3. 3)

где λ _min и λ _max – границы диапазона светового излучения.

Разницу в цветовых ощущениях оценивают порогом цветоразличения – минимально заметным для эксперта изменением цвета.

Порог цветоразличения представляет расстояние между двумя точками в системе координат цветности X', Y', соответствующее минимально различимым цветам. Но для этой системы значение порогов является функцией координат X', Y', т. е. система XYZ не является равноконтрастной. Чтобы сделать порог цветоразличения постоянным, не зависящим от координат X', Y', была разработана система UVW, полученная путем проекции плоскости X, Y на плоскость U, V под определенным углом.

Другой математический аппарат преобразования сигналов основан на теории оппонентных цветов. Цвет здесь представляет сумму трех векторов: яркости, разности " красный минус зеленый" и разности " желтый минус синий". Цветовой контраст рассчитывается как расстояние между концами векторов.

Установлены соотношения, связывающие векторные параметры с цветовым тоном и чистотой цвета.