 |
2. Случайные сигналы. Шумы. 2. 1. Параметры случайных сигналов
|
|
|
|
2. СЛУЧАЙНЫЕ СИГНАЛЫ. ШУМЫ
2. 1. Параметры случайных сигналов
Как указывалось ранее, все сигналы в природе имеют случайный характер. Их анализ и оценка осуществляется с использованием ряда статистических характеристик. Информацию о случайных сигналах получают на основе совокупности их реализаций. Реализация случайного процесса – это ставшая известной в результате приема часть сигнала. При этом все реализации должны обладать общими статистическими закономерностями [1]. Примером ряда реализаций случайного процесса можно считать отрезки радиосигнала, выделенные через определенные промежутки времени.
На рис. 2. 1 приведен ряд реализаций случайного процесса x(t). При значении t1 аргумента сигнала функция х будет принимать различные для каждой реализации значения х1. Их совокупность х1 может быть оценена одномерной плотностью вероятности p(x1, t1). Она представляет собой зависимость вероятности появления х1 от выбора значения аргумента t1.
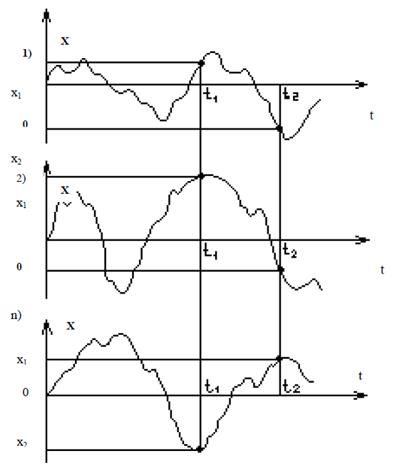
Рис. 2. 1. Реализации 1, 2, …, n случайного процесса
Для более полного описания случайного сигнала используют двумерную плотность вероятности p(x1, t1; x2, t2), показывающую зависимость вероятности появления сочетания x1 и x2 от выбора пары значений аргумента t1 и t2. При этом учитывается связь значений x1 и x2.
Увеличение мерности плотности вероятности p(x1, x2, …, xn; t1, t2, …, tn) повышает информативность, но при определенных допущениях (они будут приведены ниже) достаточным является использование двумерной плотности.
В [1] приведены вычисляемые через плотность вероятности следующие характеристики случайного процесса – математическое ожидание mx(t), дисперсия Дx(t), среднее квадратичное отклонение σ x(t).
|
|
|
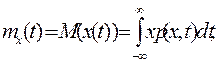
| (2. 1) | |
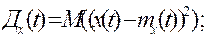
| (2. 2) | |
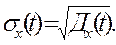
| (2. 3) |
С использованием двумерной плотности вероятности можно дополнительно определить ковариационную Kx(t1, t2) и корреляционную Rx(t1, t2) функции.
Ковариационная функция – это статистически усредненное произведение (математическое ожидание произведения) значений x(t) для координат t1 и t2:
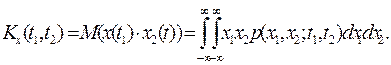
| (2. 4) |
Если t1 = t2, то
| Kx(t1, t2) = M(x2(t1)), | (2. 5) |
т. е. в данном случае ковариационная функция равна математическому ожиданию квадрата случайного сигнала при аргументе t1.
Если для исследований представляет интерес только переменная составляющая случайного сигнала, используется корреляционная функция:
| Rx(t1, t2) = M((x(t1) – mx(t1))(x(t2) – mx(t2)) = Kx(t1, t2) – mx(t1)mx(t2). | (2. 6) |
Из формулы (2. 6) видно, что при расчете Rx постоянная составляющая (математическое ожидание) вычитается.
Функции Kx(τ ) и Rx(τ ) показывают, насколько связаны между собой значения x(t) и x(τ + t).
Если t1 = t2, то
| Rx(t1, t2) = Дх(t1), | (2. 7) |
т. е при нулевом промежутке между t1 и t2 корреляционная функция равна дисперсии для значения аргумента Дх(t1).
В определенных случаях можно принять допущения о стационарности и эргодичности случайных процессов. Эти допущения упрощают расчет вероятностных параметров.
Случайный процесс является строго стационарным, если плотность вероятности p(x1, x2, …, xn; t1, t2, …, tn) п-го порядка зависит от интервалов t2 – t1, t3 – t1, …, tn – t1 и не зависит от положения этих интервалов в области изменения аргумента t [2].
Для некоторых практических приложений, например, в радиотехнике, стационарность процесса рассматривают в широком смысле. В данном случае должна отсутствовать зависимость только одномерной и двумерной плотности вероятности от аргумента t. Тогда математическое ожидание, дисперсия и среднеквадратическое отклонение не зависят от аргумента t, а ковариационная и корреляционная функция зависят только от интервала τ, равного разности t1 и t2:
|
|
|
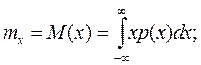
| (2. 8) | |
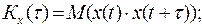
| (2. 9) | |
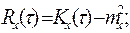
| (2. 10) | |
| Дх = M((x – mx)2) = Rx(0), | (2. 11) |
где
| τ = t2 – t1. | (2. 12) |
Иногда вместо корреляционной функции Rx(τ ) удобно использовать нормированную корреляционную функцию rx(τ ):
 .
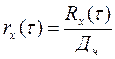| (2. 13) |
Очевидно, что rx(0) = 1.
Формулы (2. 8–2. 11) приобретают еще более простой вид, если стационарный процесс является также эргодическим. Стационарный случайный процесс является эргодическим, если при определении статистических параметров усреднение по множеству реализаций эквивалентно усреднению по аргументу t одной теоретически бесконечно длинной реализации. Для эргодических процессов
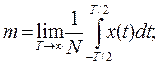
| (2. 14) | |
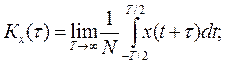
| (2. 15) | |
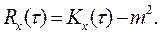
| (2. 16) |
Практически статические характеристики эргодических процессов определяются для конечной реализации. Длина реализации определяет точность их нахождения.
|
|
|
