Тема 6. Финансовые функции Microsoft Excel

Цель работы: научиться решать финансовые задачи, используя возможности программы Microsoft Excel.

Microsoft Excel содержит богатый набор финансовых функций: функции для расчета операций по кредитам и займам, для определения скорости оборота инвестиций, для расчета амортиза­ции, для расчетовпоказателей эффективности ценных бумаг.

Многие финансовые функции Microsoft Excel имеют одинаковые аргументы. В таблице 1 приведены аргументы, используемые в функциях.

Таблица 1

Аргументы финансовых функциц

Аргумент	Описание аргумента
бз бс	Будущая стоимость фиксированных периодических выплат или единой суммы
Нз, пз	начальное значение (текущая стоимость)
выплата	фиксированная периодическая выплата
Кпер, Число периодов	общее число периодов выплат
Норма	норма дисконтирования
ставка	процентная ставка за период
Тип	Число 0 или 1, обозначающее, когда производится выплата (1 - в начале периода. 0-в конце периода), по умолчанию равно 0.
предположение	предполагаемое значение процентной ставки, по умолчанию равно 0.1

 

q Функция БЗ. Определение будущей стоимости на основе постоянной процентной ставки.

Функция БЗ рассчитывает будущую стоимость периодических постоянных платежей и будущее значение единой суммы вклада или займа на основе постоянной процентной ставки.

Синтаксис БЗ (норма, число_периодов, выплата, нз, тип).

1) Будущую стоимость единой суммы вклада, по которой начисляются сложные проценты за определенное число периодов, можно рассчитать по формуле:

fv=pv*(1+r)ⁿ

где fv - будущая стоимость вклада или займа,

pv - текущая стоимость вклада или займа;

п - общее число периодов начисления процентов,

r - процентная ставка по вкладу или займу.

Для вычисления будущего значения единой суммы функция БЗ используется в виде:

=БЗ(норма, число_периодов,, нз).

В качестве разделителя аргументов используется выбранный при на­стройке Windows разделитель, обычно это запятая (,) или точка с запятой (;).

2) Периодические платежи могут осуществляться в начале каждого расчетного периода (обязательные платежи или платежи пренумерандо) или в конце (обычные пла­тежи постнумерандо) в течение n периодов. Отличие в расчете будущей совокупной стоимости таких вложений для обязательных и обычных платежей заключается в том, что во втором случае не происходит начисления процентов на последний вклад.

Для расчета будущей стоимости серии фиксированных периодических платежей пренумерандо используется формула:

fv = ртt * (1+r) + pmt * (1+r)² +... + pmt(1+r)ⁿ

= pmt * ((1+r)ⁿ –1)/r* (1+r)

где fv - будущая стоимость фиксированных периодических платежей,

pmt - фиксированная периодическая сумма платежа,

n - общее число периодов выплат;

r - постоянная процентная ставка.

Функция БЗ в данном случае используется в виде

=БЗ(норма, число_периодов, выплата,, 1).

Для расчета будущей стоимости серии фиксированных периодических платежей постнумерандо используется формула;

fv = ртt + ртt*(1+r) +... + pmt (1+r)^n-1 = pmt*((1+r)ⁿ –1)/r

Функция БЗ в данном случае используется в виде:

=БЗ(норма, число_периодов, выплата,, 0)

или

=БЗ(норма, число_периодов, выплата).

Примеры.

Задание 1. Рассчитать, какая сумма окажется на счете, если 27 тыс. руб. положены на 33 года под 13,5% годовых. Проценты начисляются каждые полгода.

Решение. Произведите расчеты двумя способами: используя финансовую формулу и с помощью финансовой функции БЗ. Для того чтобы осуществить расчет по формуле в ячейку А1 введите следующее выражение:= 27* (1+0,135/2)^(33*2), в результате получите 2012.07 тыс. руб. Для того чтобы решить задачу используя функцию БЗ, наведите курсор на ячейку А2, на панели инструментов нажмите кнопку , откроется окно Мастер функций (рис. 1.46).

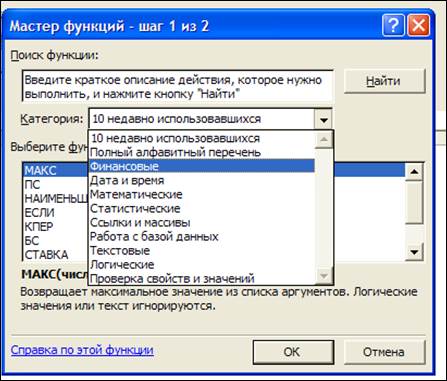
Рис 1.46. Окно мастера функций

Выберите категорию Финансовые, далее в поле Выберите функцию – функцию БЗ или БС. В открывшемся окне введите в соответствующие строки имеющиеся данные следующим образом:

Рис. 1.47. Функции БС

По условию задачи сказано, что проценты начисляются каждые полгода, поэтому необходимо значение годового процента разделить на два, в случае с периодом вклада все наоборот, количество лет надо умножить на два (рис. 1.47). Сумма первоначального вклада записывается со знаком минус, так как эта сумма является исходящим денежным потоком. В результате получили ответ = 2012,07 тыс. руб. Таким образом решение задачи двумя способами дало результат равный 2012,07 тыс.руб.

Задание 2. Есть два варианта инвестирования средств в течение 4 лет: в начале каж­дого года под 26% годовых или в конце каждого года под 38% годовых. Ежегодно вносит­ся 300 тыс. руб. Определить, сколько денег окажется на счете в конце 4-го года для каж­дого варианта.

Решение. Расчет ведется по формуле

fv = 300 *((1+0.26)^4-1)/0.26* (1+0,26) =2210.53 - для первого варианта и по формуле

fv = 300 *((1+0.38)^4-1)/0.38 =2073.74 - для второго

Используя функцию БЗ, получите:

Б3(26%, 4, -300,, 1) = 2210,53 тыс. руб. - для первого варианта,

Б3(38%,4,-300)=2073,74тыс.руб. - для второго варианта.

Расчеты показали, что первый вариант предпочтительнее.

 

q Определение текущей стоимости. Функция ПЗ.

Во многих задачах используется понятие текущей (современной) стоимости буду­щих доходов и расходов. Текущая стоимость получается как результат приведе­ния будущих доходов и расходов к начальному периоду времени (т.е. путем дисконтиро­вания).

Расчет при помощи функции ПЗ требует денежных потоков равной величины и рав­ных интервалов между операциями. Функция НПЗ допускает денежные потоки перемен­ной величины через равные периоды времени.

Синтаксис П3(норма, кпер, выплата, бс, тип).

Рассмотрим различные варианты использования этой функции при решении кон­кретных задач.

1) Допустим, известно будущее значение вклада (займа). Требуется определить текущее значение этого вклада, т.е. сумму, которую необходимо положить на счет сего­дня, чтобы в конце n-го периода она достигла заданного значения. Это значение можно получить из формулы:

pv=fv/(1+r)ⁿ

Такой же расчет при использовании функции ПЗ в общем виде запишется так

= П3(норма, кпер,, бс).

2) Расчет текущей стоимости серии будущих постоянных периодических плате­жей, производимых в начале каждого периода и дисконтированных нормой дохода r, ве­дется по формуле:

pv = ртt + ртt/(1+r) +... + pmt/(1+r)^n-1 =pmt(1-1/(1+r)ⁿ)/r*(1+r)

где pv - текущая стоимость серии фиксированных периодических платежей,

pmt - фиксированная периодическая сумма платежа,

п - общее число периодов выплат (поступлений),

r - постоянная процентная ставка.

Для расчета этой величины функция ПЗ используется в виде:

=ПЗ(норма, кпер, выплата,, 1).

3) Для расчета текущей стоимости постоянных периодических выплат, если они происходят в конце периода, используется формула:

pv = ртt/(1+r) + ртt/(1+r)² +...+ pmt/(1+r)ⁿ =pmt(1-1/(1+r)ⁿ)/r

Соответствующая этому расчету формула в EXCEL имеет вид:

=ПЗ(Hоpмa, кпер, выплата).

По умолчанию аргумент тип равен 0, поэтому его можно не указывать.

Примеры.

Задание 1. Фирме потребуется 5000 руб. через 12 лет, В настоящее время фирма располагает деньгами и готова положить их на депозит единым вкладом, чтобы через 12 лет он достиг 5000 руб. Определить необходимую сумму текущего вклада, если ставка про­цента по нему составляет 12% в год.

Решение. Для расчета используем формулу (2.1) или следующую функцию:

П3(12%, 12,,5000)= -1283,38руб.

Результат получился отрицательный, так как это сумма, которую необходимо вло­жить.

Задание 2. Рассматривается два варианта покупки дома: заплатить сразу 99000 руб. или в рассрочку - по 940 руб. ежемесячно в течение 15 лет. Определить, какой вариант предпочтительнее, если ставка процента - 8% годовых.

Решение. В задаче необходимо сравнить, что выгоднее: заплатить сегодня указанную сумму или растянуть платежи на определенный срок. Для сравнения следует привести эти денежные потоки к одному периоду времени, т.е. рассчитать текущую стоимость будущих фиксированных периодических выплат. Допустим, что выплаты происходят в конце каж­дого расчетного периода, Расчет можно вести по формуле (2.3) или используя функцию ПЗ:

П3(8%/12, 15*12, -940) = 98362,16 руб.

Запрашиваемая цена 99000 руб. больше рассчитанной текущей стоимости периоди­ческих выплат, следовательно, невыгодно покупать дом сразу, лучше растянуть платежи на 15 лет.

 

□ Определение текущей стоимости. Функция НПЗ.

Функция НПЗ вычисляет чистую текущую стоимость (NPV) периодических плате­жей переменной величины как сумму ожидаемых расходов и доходов, дисконтированных нормой процента r.

Метод определения чистой текущей стоимости часто применяется при оценке эф­фективности инвестиций. Он позволяет определить нижнюю границу прибыльности и ис­пользовать ее в качестве критерия при выборе наиболее эффективного проекта. Дискон­тирование ожидаемых доходов и расходов позволяет учесть издержки привлечения капи­тала. Положительное значение NPV является показателем того, что проект приносит чис­тую прибыль своим инвесторам после покрытия всех связанных с ним расходов.

Синтаксис НПЗ(норма, сумма1, сумма2,..., cyммaN).

Считается, что инвестиция, чистую текущую стоимость которой вычисляет функция НПЗ, начинается за один период до даты аргумента сумма1 и заканчивается с последним значением в списке. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить (вычесть, если это затраты) к результату функции НПЗ, но не включать в список аргументов

Примеры

Задание 1. Инвестиции в проект к концу первого года его реализации составят 10000 руб. В последующие три года ожидаются годовые доходы по проекту 3000 руб., 4200 руб., 6800 руб. Издержки привлечения капитала 10%. Рассчитать чистую текущую стоимость проекта.

Решение. Так как инвестиция размером 10000 руб. относится не к начальному мо­менту, на который производится расчет, то это значение следует включить в список аргу­ментов. Поскольку этот денежный поток движется "от нас", то сумма 10000 руб. записывается со знаком “-“. Остальные денежные потоки представляют доходы, поэтому имеют знак "+". Чистый текущий объем инвестиции составит:

НПЗ(10%, -10000, 3000, 4200, 6800) = 1188,44 руб

Вычисленное значение представляет абсолютную прибыль от вложения 10000 руб. через год с учетом издержек привлечения капитала.

Задача 2. Допустим, затраты на проект в начальный момент его реализации состав­ляют 37000 руб., а ожидаемые доходы за первые пять лет: 8000 руб, 9200 руб., 10000 руб., 13900 руб. и 14500 руб. На шестой год ожидается убыток в 5000 руб. Цена капитала 8% годовых. Рассчитать чистую текущую стоимость проекта.

Решение. В этой задаче нет необходимости дисконтировать начальные затраты по проекту, так как они относятся к настоящему моменту, и их текущая стоимость равна 37000 руб. Для сравнения затрат с будущими доходами и убытками последние необходи­мо привести к начальному моменту. Если доходы ввести в ячейки В1:В5 соответственно, чистая текущая стоимость проекта составит:

НПЗ(8%, B1:B5, -5000) - 37000 = 3167.77 руб.

 

q Определение срока платежа. Функция КПЕР.

Функция КПЕРвычисляет общее число периодов выплат как для единой суммы вклада (займа), так и для периодических постоянных выплат на основе постоянной про­центной ставки. Если платежи производятся несколько раз в год, найденное значение не­обходимо разделить на число расчетных периодов в году, чтобы найти число лет выплат.

Синтаксис. КПЕР(норма, выплата, нз, бс, тип).

Функция может применяться в следующих расчетах.

1) Если рассчитывается общее число периодов начисления процентов, необходи­мых для того, чтобы начальная сумма размером НЗ достигла будущего значения БС, то функция используется в виде:

КПЕР(норма,, нз, бс).

2) Формула для расчета общего числа периодов, через которые совокупная величи­на фиксированных периодических выплат составит значение БС, получается в виде:

КПЕР(норма, выплата,, бс, 1)

если платежи производятся в начале каждого расчетного периода, и в виде:

КПЕР(норма, выплата,, бс,)

для выплат в конце периода.

3) При погашении займа размером НЗ равномерными постоянными платежами в конце каждого периода число периодов, через которое произойдет полное погашение, равно

КПЕР(норма, выплата, нз).

Полученное значение можно также использовать как показатель срока окупаемости при анализе инвестиционного проекта. При этом предполагается, что поступление дохо­дов происходит периодически равными величинами в конце или в начале каждого расчет­ного периода. Рассчитанное значение будет представлять число расчетных периодов, че­рез которое сумма доходов, дисконтированных на момент завершения инвестиций, будет равна величине инвестиций.

Примеры.

Задание 1. Рассчитать, через сколько лет вклад размером 1 тыс. руб. достигнет вели­чины 1 млн. руб., если годовая ставка процента по вкладу 16.79% и начисление процентов производится ежеквартально.

Решение. Функция КПЕР дает следующий резуль­тат:

КПЕР(16,79% / 4,, -1, 1000) = 168 - это число кварталов.

Число лет составит 168 / 4=42.

Задание 2. Для обеспечения будущих расходов создается фонд. Средства в фонд по­ступают в виде постоянной годовой ренты постнумерандо. Размер разового платежа 16 тыс. рублей. На поступившие взносы начисляется 11,18% годовых. Необходимо опреде­лить, когда величина фонда будет равна 100 тыс. рублей.

Решение. Для решения задачи необходимо вычислить величину n. В EXCEL этот расчет выглядит так

КПЕР(11.18%,-16,, 100)=5, т. е, через 5 лет совокупная величина выплат составит 100 тыс. руб.

Задание 3. Ожидается, что ежегодные доходы от реализации проекта составят 33 тыс. руб. Необходимо рассчитать срок окупаемости проекта, если инвестиции к началу посту­пления доходов составят 100 тыс руб., а норма дисконтирования 12.11%

Решение. В задаче требуется определить, через сколько лет текущая стоимость ожи­даемых доходов будет равна величине инвестиций. Срок окупаемости будет равен:

КПЕР(12.11%,33,-100)=4 года.

 

q Расчет процентной ставки. Функция НОРМА.

Функция НОРМА определяет значение процентной ставки за один расчетный пери­од. Для нахождения годовой процентной ставки полученное значение следует умножить на число расчетных периодов, составляющих год.

Синтаксис. НОРМА (кпер, выплата, нз, бс, тип, предположение).

Функция НОРМА вычисляется методом последовательного приближения и может не иметь решения или иметь несколько решений. Если после 20 итераций погрешность опре­деления ставки превышает 0,0000001, то функция НОРМА возвращает значение ошибки #ЧИСЛО1. В этом случае можно попытаться задать другой аргумент предположение, по умолчанию равный 10%. В большинстве случаев не требуется задавать аргумент предпо­ложение.

Рассмотрим варианты практического применения этой функции

1) Допустим, необходимо рассчитать процентную ставку при известной текущей стоимости НЗ, будущей стоимости БС, числе периодов КПЕР. Тогда формула в EXCEL в общем виде записывается так:

НОРМА (кпер,, нз, бс,, предположение).

2) В случае фик­сированных обязательных или обычных периодических платежей процентную ставку за расчетный период удобнее вычислять с помощью функции:

НОРМА(кпер, выплата,, бс, тип, предположение).

3) Расчет процентной ставки по займу размером НЗ при равномерном погашении обычными периодическими платежами, при условии, что заем полностью погашается, ве­дется по формуле:

НОРМА (кпер, выплата, нз,,, предположение).

Примеры.

Задание 1. Предположим, что компании потребуется 100 тыс. руб. через 2 года. Ком­пания готова вложить 5 тыс. руб. сразу и по 2,5 тыс. руб. каждый последующий месяц. Каким должен быть процент на инвестированные средства, чтобы получить необходимую сумму в конце второго года.

Решение. В этой задаче сумма 100 тыс. руб. (аргумент БС функции НОРМА) форми­руется за счет приведения к будущему моменту начального вклада размером 5 тыс. руб. (аргумент НЗ) и фиксированных ежемесячных выплат (аргумент выплата). Используем функцию:

НОРМА(24, -2,5, -5, 100)= 3,28%.

Ежемесячная процентная ставка составит 3,28%, годовая – 12*3,28%=39,36%

Задание 2. Рассчитайте процентную ставку для четырехлетнего займа в 7000 руб. с ежемесячным погашением по 250 руб. при условии, что заем полностью погашается.

Решение. Будущее значение ежемесячных выплат по 250 руб. должно составить че­рез 4 года сумму займа с процентами. Ежемесячная ставка процента должна составлять

НОРМА(48, -250, 7000) =2.46%,

Годовая процентная ставка составит 2.46% * 12 = 29.5%,

 

q Расчет периодических платежей. Функция ППЛАТ.

Функция ППЛАТ вычисляет величину выплаты за один период на основе фиксиро­ванных периодических выплат и постоянной процентной ставки. Выплаты, рассчитанные функцией ППЛАТ, включают основные платежи и платежи по процентам.

Синтаксис ППЛАТ (норма, кпер, нз, бс, тип).

Функция ППЛАТ применяется в следующих расчетах

1. Допустим, известна будущая стоимость фиксированных периодических выплат, производимых в начале или в конце каждого расчетного периода. Требуется рассчитать размер этих выплат Для этого можно использовать формулу

ППЛАТ(норма, кпер., бс, тип).

2. Предположим, рассчитываются равные периодические платежи по займу вели­чиной НЗ, необходимые для полного погашения этого займа через КПЕР число периодов. Текущая стоимость этих выплат должна равняться текущей сумме займа. Расчет в EXCEL выполняется по формуле;

ППЛАТ(норма, кпер, нз,, тип).

Обычно погашение происходит в конце каждого расчетного периода. Для этого слу­чая формула имеет вид:

ППЛАТ(норма, кпер, нз), так как аргумент тип - 0,

Если заем погашается не полностью, то есть его будущее значение не равно 0, то следует указать аргумент БС, который равен непогашенному остатку займа после всех вы­плат.

Примеры.

Задание 1. Предположим, что необходимо накопить 4000 руб. за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой должна быть эта сумма, если норма процента по вкладу составляет 12% годовых.

Решение. Общее число периодов начисления процентов кпер =3*12, норма = 12% / 12. Аргумент тип = 0, т.к. это вклады постнумерандо. Величина ежемесячных выплат бу­дет равна:

ППЛАТ(12%/12, 12*3„4000)=-92,86руб.

Задание 2. Допустим, банк выдал ссуду 200 тыс. руб. на 4 года под 18% годовых. Ссуда выдана в начале года, а погашение начинается в конце года одинаковыми платежа­ми. Определить размер ежегодного погашения ссуды

Решение. Ежегодные платежи составят ППЛАТ(18%, 4, -200) = 74,35 тыс. руб.

 

Контрольные вопросы

Для расчета каких значений используется функция БЗ?

Какие данные необходимо иметь для того, чтобы произвести расчет по функции НЗ?

В чем различие между аргументами «Начальное значение» и «Выплата»?

Что означает «платеж пренумерандо»?

С помощью какой функции можно определить процент начислений по кредиту?

 

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПО ТЕМЕ 6

Задача 1. Пользователь Сбербанка внес вклад 5 млн. рублей. До какой суммы воз­растет вклад через 7 лет, если процент годовых начислений равен а) 6 %, б) 10 %, в) 15%.

Задача 2. Вскоре после рождения сына родители решили внести в Сбербанк вклад с тем, чтобы через 22 года вклад вырос до суммы 30 млн. руб. Каков должен быть вклад, если процент годовых начислений равен 5 %, 8 %, 10%.

Задача 3. Через сколько лет начальный вклад 1000 $ увеличится до суммы 3000$, 5000 $ или 8000 $, если процент годовых начислений равен 6 %.

Задача 4. Какой процент годовых начислений должен обеспечить банк, чтобы первоначаль­ный вклад 5000 $ увеличился втрое за 15, 18, 20 лет.

Задача 5. Рассчитать процентную ставку для 3-летнего займа размером 5000 руб. с еже­квартальным погашением по 1500 руб.

Задача 6. Определить эффективность инвестиции размером 200 млн, руб. по NPV, если ожидаемые ежемесячные доходы за первые пять месяцев составят соответственно: 20, 40, 50, 80 и 100 млн. руб. Издержки привлечения капитала составляют 13,5% годовых.

Задача 7. Определить, какие ежемесячные выплаты необходимо вносить по ссуде разме­ром 200 тыс. руб., выданной на три года, при разных процентных ставках. Использовать Таблицу подстановки Excel.

Задача 8. Вкладчик Сбербанка решил ежегодно вносить вклад 1000$ в течение 10 лет. Сколько денег он сможет получить, если процент годовых начислений равен 5%, 10%, 15%.

Задача 9. Пусть вы откладываете 500 $ в конце каждого года на сберегательный счет при ставке 15 % годовых. Определить сумму накоплений к концу 6-го года.

Задача 10. Семья решила накопить для покупки дома сумму 20 000 $, вкладывая ежегодно сумму 1000$ (1500$ или 2000$). Сколько лет на это потребуется, если процент годовых начислений равен 6 %.

Задача 11. Какую сумму должен ежегодно вносить вкладчик, чтобы через 5 (10 или 15) лет накопить сумму 15000 $ при проценте годовых 3 %.

Задача 12. Каким должен быть процент годовых начислений, чтобы при ежегодном вкладе 1000 $ (1 500 $ или 3000 $) накопить сумму 20 000 $ за 15 лет.

Задача 13. Известно, что за 4 месяца вклад одного из вкладчиков Сбербанка увеличился с 4 млн. рублей до 6 млн. рублей. До какой суммы возрастет этот вклад через один год и через два года.

Задача 14. Вскоре после рождения сына родители решили внести в Сбербанк вклад с тем, чтобы через 22 года вклад вырос до суммы 30 млн. руб. Каков должен быть вклад, если процент годовых начислений равен 5 %, 8 %, 10%.

Задача 15. Рассматриваются два варианта покупки недвижимости: заплатить всю сумму сразу - 70 000 руб. или платить ежемесячно по 800 руб. в течение 12 лет при ставке 9% годовых. Какой вариант более выгоден (68 743)?

Задача 16. Вексель на 3 000 000 долл. с годовой учетной ставкой 10% с дисконтированием два раза в год выдан на два года. Найти исходную сумму, выданную под этот вексель.

Задача 17. На счет в банке вносится сумма 10 000 долл. в течение 10 лет равными долями в конце каждого года. Ежемесячная ставка 4%. Какая сумма будет на счете через 10 лет?

Задача 18. Сумма 2000 долл. размещена под 9% годовых на три года. Проценты начисляются раз в квартал. Какая сумма будет на счете на конец периода договора.

Задача 19. Банк принимает вклад на срок 3 месяца с объявленной годовой ставкой 100% (140 625) или на 6 месяцев под 110% (169 254). Как выгоднее будет вложить сумму в 100 000 руб. на полгода: дважды на три месяца (проценты начисляются в начале квартала) или один раз на 6 месяцев (проценты начисляются ежемесячно)?

Задача 20. Получена ссуда в 20 000 долл. дана на полтора года под ставку 28% годовых с ежеквартальным начислением. Определить какую сумму необходимо будет вернуть кредитору.

Задача 21. Выдан кредит в сумме 1 млн. долл. с 15.01.04 по 15.03.04 под 120% годовых. Рассчитать сумму погасительного платежа.

Задача 22. Под темпом инфляции понимают относительный прирост цен за период. Фраза «инфляция идет в темпе 10% в месяц» означает, что имеет место схема сложных процентов, этапом в которой является месяц, за каждый месяц цены увеличиваются на 10%. Рассчитать стоимость заданного товара через 1 год при темпе инфляции 10% в год, 3% в месяц и 1% в месяц, если в начале года цена товара составляла 50 000 рублей.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: