Контур с током в магнитном поле

Рассмотрим более подробно поведение контура с током в магнитном поле. Допустим, что в однородном поле находится контур с током I. По закону Ампера на каждый элемент контура действует сила

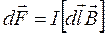(18.23)

Результирующая этих сил

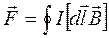(18.24)

Поскольку I и 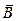постоянны, их можновынести за знак интеграла:

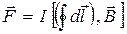(18.25)

Но интеграл очевидно равен нулю, а значит результирующая, сила, действующая на контур с током в однородном магнитном поле также равна нулю. Это утверждение справедливо для произвольного контура в однородном поле.

Ограничимся рассмотрением плоских контуров.Пусть плоский контур – рисунок 2 – ори­ентирован так, что положительная нормаль к контуру перпендикулярна к век­тору индукции однородного магнитного поля. (Положительной называется нормаль, направление которойсвязано с направлением тока в контуре прави­лом правого винта.) Вычислиммомент сил действующих на контур. Разобьем контур на полоски шириной 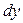, параллельные вектору . 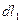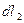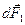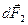На ограничивающие подоску эле­менты контура и действуют силы и - направленные перпендикулярно плоскости чертежа в противоположные стороны. Модули этих сил равны по закону Ампера

,

Таким образом, силы 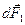и 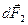-образуют пару, момент которой

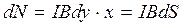(18.25)

Очевидно, что 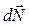перпендикулярен 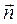и ,а значит можно записать:

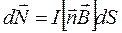(18.26)

Суммируя по всем полоскам, на которые разбивается контур, получаем:

(18.27)

Выражение (18.27) можно представить в виде:

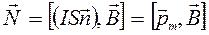(18.28)

где - дипольный магнитный момент контура с током.

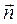Мы рассмотрели ситуацию, когда вектор индукции магнитного поля лежал в плоскости контура. Если направление и 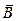совпадают, то силы, действующие на элементыконтура, лежат в плоскости контура, и вращательного момента не создают. Они лишь стремятся растянуть контур. Если направления 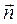и 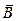противоположны, то возникающие силы стремятся сжать контур.

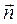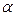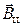Допустим, что и составляют угол . Тогда можно разложить на и . Составляющая обу­словливает только растяжение или сжатие контура, а зна­чит:

(18.29)

Из рисунка 3 видно,

(18.30)

Таким образом, в общем случае на плоский контур в магнитном поле действует момент сил

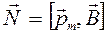(18.31)

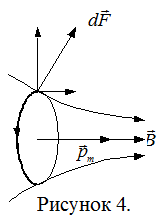Рассмотрим теперь, что происходит с плоским контуром с током в неодно­родном магнитном поле. Для упрощение рассуждений будем считать контур кру­говым. Допустим также, что поле наиболее быстро изменяется вдоль направ­ления оси х, которое совпадает с направлением в том месте, где находится центр контура, а магнит­ный момент контура ориентирован по полю. Сила 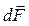, действующая на элемент контура должна быть перпендикулярна , а значит и силовой линии. Таким образом, силы, приложенные к различным эле­ментам контура, образуют симметричный конический ве­ер. Результирующая этих сил направлена в сторону возрастания , а значит, контур будет втягиваться в область более сильного поля. Чем больше величина , тем больше результирующая сила.

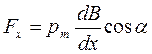
Если развернуть контур на 180⁰ (изменить направление тока в контуре на обратное), то станет противоположным и результирующая сила будет направлена в сторону убывания поля.

10 Магнитное поле контура с током

Воспользуемся законом БСЛ для расчета поля, создаваемого круговым током на его оси. Векторы 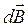создаваемые элементами пер­пендикулярны плоскости, прохо­дящей через и точку наблюде­ния, образуют симметричный ко­нический веер. Из соображений симметрии ясно, что результирующее поле на­правлено вдоль оси контура. Каждый из векторов 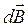вносит в результирую­щий вектор составляющую

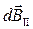
(18.32)

Интегрируя по всему контуру, получаем:

 

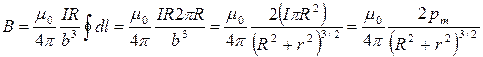(18.33)

 

Поскольку векторы и направлены одинаково, то можно записать в векторном виде:

(18.35)

Примечательно, что (18.35) не зависит от знака r. Следовательно в симмет­ричных относительно контура точках имеет одинаковую величину и на­правление.

Положив r=0, получим формулу для индукции в центре кругового тока:

(18.36)

На больших расстояниях от контура в знаменателе можно пренебречь R по сравнению с r. Тогда получим:

(18.37)

Примерный вид линий вектора индукции поля кругового тока показан на рисунке 6.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: