 |
Контур без активного сопротивления.
|
|
|
|
Закон Ома и правила Кирхгофа установлены и, строго говоря, справедливы для постоянного тока. Однако, они остаются практически справедливыми и для мгновенных значений изменяющихся токов и напряжений, если их изменения происходят не слишком быстро. Если за время t, распространения электромагнитного возмущения по длине l всей цепи, сила тока изменяется незначительно, то такие токи называются квазистационарными. Математически для периодически изменяющихся токов условие квазистационарности имеет вид:
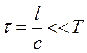 (21.01)
(21.01)
Т - период.
Для квазистационарных токов закон Ома справедлив и мы будем рассматривать только такие токи.
 Простейшей цепью, в которой могут возникнуть электрические колебания, является цепь, состоящая из ёмкости С и индуктивности L. Колебания в контуре можно вызвать либо сообщив конденсатору начальный заряд, либо возбудив в индуктивности индукционный ток, например, выключив внешнее магнитное поле.
Простейшей цепью, в которой могут возникнуть электрические колебания, является цепь, состоящая из ёмкости С и индуктивности L. Колебания в контуре можно вызвать либо сообщив конденсатору начальный заряд, либо возбудив в индуктивности индукционный ток, например, выключив внешнее магнитное поле.
Например, рассмотрим процессы при замыкании заряженного конденсатора на катушку индуктивности. Будем считать, что сопротивление проводников схемы равно нулю.
1. 
 В начальный момент времени энергия системы сосредоточена в электрическом поле конденсатора. При замыкании цепи в цепи возникает электрический ток, возбуждающий в катушке нарастающее магнитное поле, с которым оказывается связанной часть запасенной конденсатором энергии. В катушке возбуждается ЭДС самоиндукции, которая противодействует нарастанию тока, в соответствии с правилом Ленца. Ток продолжает нарастать (энергия переходит в энергию магнитного поля катушки) и достигает максимального значения при полном разряде конденсатора. При этом изменение тока прекращается, ЭДС самоиндукции обращается в нуль. Вся запасенная конденсатором энергии преобразуется в энергию магнитного поля в катушке индуктивности. По времени описанные процессы составляют четверть периода электромагнитного колебания в контуре.
В начальный момент времени энергия системы сосредоточена в электрическом поле конденсатора. При замыкании цепи в цепи возникает электрический ток, возбуждающий в катушке нарастающее магнитное поле, с которым оказывается связанной часть запасенной конденсатором энергии. В катушке возбуждается ЭДС самоиндукции, которая противодействует нарастанию тока, в соответствии с правилом Ленца. Ток продолжает нарастать (энергия переходит в энергию магнитного поля катушки) и достигает максимального значения при полном разряде конденсатора. При этом изменение тока прекращается, ЭДС самоиндукции обращается в нуль. Вся запасенная конденсатором энергии преобразуется в энергию магнитного поля в катушке индуктивности. По времени описанные процессы составляют четверть периода электромагнитного колебания в контуре.
|
|
|
2. Однако ток в цепи не прекращается, вследствие того, что ЭДС самоиндукции изменяет знак на противоположный и поддерживает его. Протекая в прежнем направлении, ток начинает заряжать конденсатор, но полярность зарядов на обкладках конденсатора меняется на противоположную. Энергия системы начинает преобразовываться из энергии магнитного поля в энергию электрического поля конденсатора. Процесс подзарядки конденсатора продолжается до полного перехода энергии в поле конденсатора. Напряжение на конденсаторе достигает максимального значения, равного исходному, но имеет противоположную полярность. По времени описанные процессы составляют вторую четверть периода электромагнитного колебания в контуре.
3. В третьей четверти периода процессы в контуре повторяют первую, но начинаются с заряженного состояния конденсатора, отличающегося обратной полярностью.
4. В четвертой четверти процессы аналогичны второй, но конденсатор и система возвращаются в исходное состояние.
Найдём уравнение колебаний в таком контуре.
Условимся считать положительным ток, заряжающий конденсатор: 
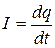 . (21.02)
. (21.02)
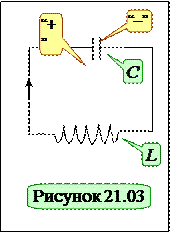 Тогда по второму правилу Кирхгофа падение напряжения на активном сопротивлении цепи должно быть равно сумме ЭДС, действующих в контуре. В контуре имеется конденсатор, напряжение, на котором
Тогда по второму правилу Кирхгофа падение напряжения на активном сопротивлении цепи должно быть равно сумме ЭДС, действующих в контуре. В контуре имеется конденсатор, напряжение, на котором  можно рассматривать, как ЭДС, которую следует взять в сумме «с минусом», поскольку она напрвлена навстречу току зарядки конденсатора. К этой ЭДС необходимо добавить ЭДС самоиндукции
можно рассматривать, как ЭДС, которую следует взять в сумме «с минусом», поскольку она напрвлена навстречу току зарядки конденсатора. К этой ЭДС необходимо добавить ЭДС самоиндукции 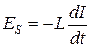 . Поэтому уравнение по второму правилу Кирхгофа следует записать в виде:
. Поэтому уравнение по второму правилу Кирхгофа следует записать в виде:
 (21.03)
(21.03)
Подставим в (21.03) выражения для ЭДС и учтем, что по предположению в контуре нет активного сопротивления:
|
|
|
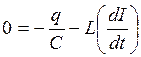 . (21.04)
. (21.04)
Но по определению силы тока
 . (21.05)
. (21.05)
Поэтому уравнению (21.04) можно придать вид:
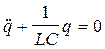 . (21.06)
. (21.06)
Уравнение точно такого вида мы решали при рассмотрении механических колебаний. Положив  , получим
, получим
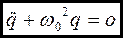 . (21.07)
. (21.07)
Решение (21.07) имеет вид
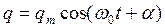 . (21.08)
. (21.08)
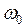 называется: собственной частотой контура.
называется: собственной частотой контура.
Период колебаний определяется по формуле Томпсона
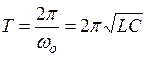 . (21.09)
. (21.09)
Напряжение на конденсаторе изменяется по закону:
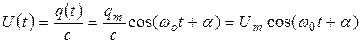 . (21.10)
. (21.10)
Дифференцируя (21.08) по времени, найдём для силы тока:
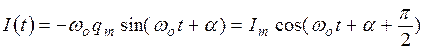 . (21.11)
. (21.11)
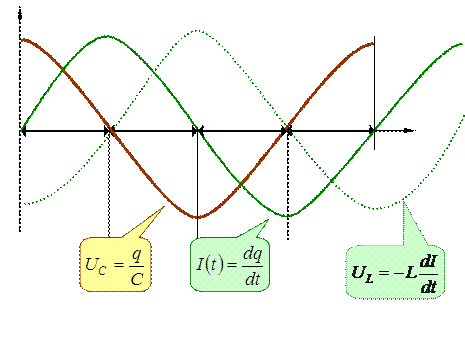
Сравнивая (21.10)и (21.11), видим, что сила тока опережает по фазе напряжение на конденсаторе на p/2. Когда ток достигает максимума, напряжение обращается в нуль и наоборот. С учетом именно этого утверждения построены графики на рисунке 1.
Представляет интерес рассмотреть отношение максимального напряжения на конденсаторе 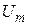 к максимальному току
к максимальному току 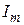 . Это отношение имеет размерность сопротивления и называется характеристическим сопротивлением контура. Поскольку
. Это отношение имеет размерность сопротивления и называется характеристическим сопротивлением контура. Поскольку 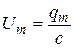 , а
, а  , то
, то
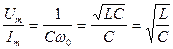 . (21.12)
. (21.12)
следовательно,
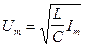 . (21.13)
. (21.13)
Затухающие колебания.
Во всяком реальном контуре обязательно присутствует активное сопротивление R. Соответственно выражение для закона Ома будет иметь вид (21.03):
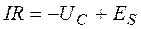 или
или 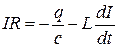 . (21.14)
. (21.14)
Разделим (21.14) на 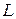 и воспользуемся обозначением:
и воспользуемся обозначением:
 . (21.15)
. (21.15)
Получаем дифференциальное уравнение, описывающее колебания в контуре с ненулевым активным сопротивлением:
 (21.16)
(21.16)
Параметр 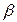 называется коэффициентом затухания. По смыслу эта величина обратна времени, в течение которого амплитуда колебаний уменьшается в «е» раз.
называется коэффициентом затухания. По смыслу эта величина обратна времени, в течение которого амплитуда колебаний уменьшается в «е» раз.
Решение (21.16) при не слишком большом затухании имеет вид (как известно!):
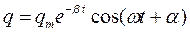 (21.17)
(21.17)
«…при не слишком большом затухании» означает:
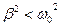 . (21.18)
. (21.18)
В этом случае циклическая частота колебаний остается вещественной:
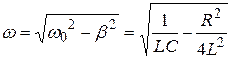 . (21.19)
. (21.19)
Из (21.19) следует, что частота затухающих (т.е. при ненулевом сопротивлении в контуре) колебаний меньше собственной.
Для характеристики степени затухания колебаний используют логарифмический декремент затухания, который определяется соотношением:
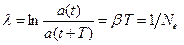 . (21.20)
. (21.20)
Напомним, что 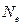 есть количество колебаний, совершаемых системой за время, пока амплитуда колебаний уменьшается в «е» раз.
есть количество колебаний, совершаемых системой за время, пока амплитуда колебаний уменьшается в «е» раз.
В нашем случае 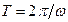 и
и 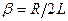 , поэтому
, поэтому
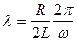 . (21.21)
. (21.21)
поскольку 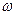 определяется параметрами контура
определяется параметрами контура 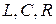 , то логарифмический декремент затухания l является характеристикой контура. Важно отметить, что соотношение (21.21) справедливо всегда, в отличии от широко используемого приближенного соотношения, которое мы сейчас рассмотрим.
, то логарифмический декремент затухания l является характеристикой контура. Важно отметить, что соотношение (21.21) справедливо всегда, в отличии от широко используемого приближенного соотношения, которое мы сейчас рассмотрим.
|
|
|
При небольшом затухании 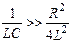 ,и вторым слагаемым в (21.19) можно пренебречь. Тогда
,и вторым слагаемым в (21.19) можно пренебречь. Тогда
 . (21.22)
. (21.22)
 . (21.23)
. (21.23)
Чаще для характеристики степени затухания колебаний используется добротность контура:
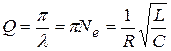 . (21.24)
. (21.24)
Добротность контура, как и любой колебательной системы, пропорциональна 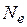 .
.
Энергия, запасённая в контуре, пропорциональна квадрату напряжения на конденсаторе, а значит, уменьшается по закону:
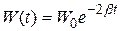 . (21.25)
. (21.25)
Тогда отношение энергии DW, теряемой в контуре за период к запасённой 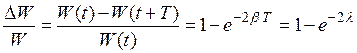 . (21.26)
. (21.26)
Если (!) затухание невелико: l << 1, то 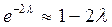 , а значит
, а значит
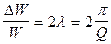 . (21.27)Отсюда находим, что
. (21.27)Отсюда находим, что
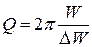 . (21.27)
. (21.27)
Другими словами добротность пропорциональна отношению энергии запасённой в контуре к энергии, теряемой за период.
|
|
|


