Природа возникновения ЭДС индукции

Рассмотрим ситуацию, когда ЭДС индукции возникает в контуре, показанном на рисунке при перемещении подвижной стороны контура с некоторой скоро-

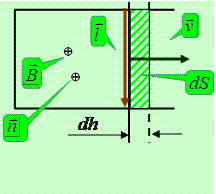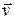стью . Вместе с перемычкой с той же скоростью движутся все электроны внутри нее, и на каждый в магнитном поле действует сила Лоренца, направленная вдоль перемычки:

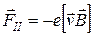
Действие этой силы эквивалентно действию силы со стороны электрического поля с напряженностью

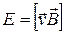. (20.1)

Это поле не имеет электростатической природы, и циркуляция вектора напряженности по контуру дает величину ЭДС, действующей в контуре:

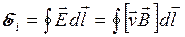. (20.2)

При вычислении интеграла в (20.2) примем за положительное направление обхода контура направление по часовой стрелке. Тогда положительная нормаль к контуру будет направлена так же, как вектор индукции магнитного поля. Элементы в подвижной рамке, в которых собственно действует поле, создающее ЭДС в сумме дают вектор 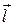. Векторное произведение 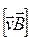является постоянной величиной в пределах подвижной части контура. Поэтому

. (20.3)

В смешанном произведении векторов в соотношении (20.3) можно провести циклическую перестановку векторов:

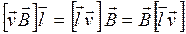. (20.4)

Умножим и разделим это выражение на 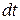. Тогда для ЭДС индукции получим:

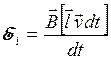. (20.5)

Вектор 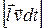по модулю равен площади, описанной подвижной частью за время 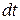, однако направлен «к нам». Вектор направлен по направлению нормали к контуру. Поэтому

. (20.6)

Соотношение (20.7)

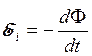. (20.7)

называют обычно законом Фарадея или законом ЭМИ.

Таким образом, в рассматриваемом случае, т.е. при движении проводника в магнитном поле, возникновение ЭДС индукции объясняется действием силы Лоренца на носители заряда в проводнике. В этом объяснении имеется существенный недостаток: индукционный ток проходя по проводникам совершает некоторую работу, а сила Лоренца работы совершать не может.

Это противоречие является кажущимся. Электроны под действием силы Лоренца приходят в движение со скоростью 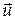, направленной по вектору 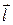. Это движение вызывает появление второй составляющей силы Лоренца , направленной навстречу скорости движения подвижной части контура. Для поддержания движения со скоростью 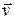к подвижной стороне необходимо будет прикладывать силу. Эта сила и совершает ту работу, которая выделяется в проводах контура при протекании по нему индукционного тока.

Сила совершает отрицательную работу, равную положительной работе составляющей силы Лоренца 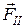. Действительно, за время 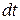полная работа силы Лоренца

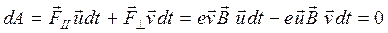. (20.8)

Часто бывает так, что контур образован не одним витком, а несколькими. По сути дела именно такая ситуация реализуется, например, во всех трансформаторах. Витки соединяются последовательно, и ЭДС в таком контуре равна сумме ЭДС в каждом из витков:

. (20.8)

Величина

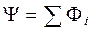(20.9)

называется потокосцеплением.

Токи Фуко

Индукционные токи могут возникать не только в контурах, но и в сплошных массивных проводниках. Действительно, всякий сплошной проводник можно представить состоящим из большого количества замкнутых контуров. В этом случае индукционные токи называют вихревыми или токами Фуко.

По правилу Ленца вихревые токи направлены так, чтобы противодействовать причине их вызывающей. Поэтому движущиеся в магнитном поле сплошные проводники испытывают сильное торможение, величина которого зависит от скорости движения. Это используют, например, для торможения подвижных частей стрелочных приборов. При этом торможение уменьшается по мере приближения стрелки к положению равновесия.

В индукционных печах вихревые токи обеспечивают разогрев металлов до плавления.

Однако в трансформаторах индукционные токи приводят к дополнительным потерям энергии на разогрев сердечника, и с ними борются, набирая сердичники из изолированных пластин.

При протекании по проводам тока создается магнитное поле, и носители заряда движутся в этом поле. Если ток переменный, то возникающие токи Токи Фуко увеличивают его вблизи поверхности провода и уменьшают в центре. В результате большая часть переменного тока протекает по поверхности проводника. Это явление называют поверхностным, или скин-эффектом.

Явление самоиндукции

Явление самоиндукции является частным случаем явления электромагнитной индукции. Если в некотором контуре протекает электрический ток, то он создает магнитное поле и магнитный поток через поверхность контура. При изменениях тока изменяется магнитный поток, и возникает ЭДС индукции противодействующая этому изменению по правилу Ленца. Ее и называют ЭДС индукции .

Величина индукции магнитного поля, а значит и магнитный поток через его поверхность, пропорциональны протекающему току:

. (20.10)

Коэффициент пропорциональности в формуле (20.10) называется индуктивностью контура. Единицей индуктивности является 1 генри (Гн).

Индуктивность определяется геометрическими параметрами контура и магнитными свойствами окружающей среды. Для того, чтобы более конкретно представить влияние на величину индуктивности этих факторов вычислим индуктивность соленоида, близкого к идеальному, т.е. с длиной 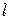, большой по сравнению с геометрическими размерами сечения, имеющего площадь (). Индукция магнитного поля соленоида при силе тока в нем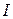

(20.11)

где 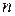- количество витков на единицу длины соленоида;

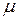- магнитная проницаемость среды внутри соленоида.

Количество витков в соленоиде 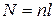, и через каждый из них магнитное поле создает поток

. (20.12)

Потокосцепление (полный поток)

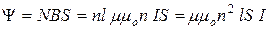. (20.13)

Очевидно, что индуктивность соленоида выражается соотношением

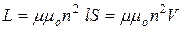, (20.14)

где 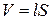есть объем соленоида.

Если в области действия магнитного поля ферромагнетики отсутствуют, то магнитная проницаемость остается постоянной и ЭДС индукции

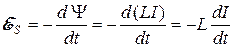. (20.15)

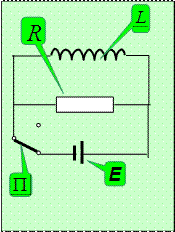
20.5. Токи при замыкании и размыкании цепи с индуктивностью

Влияние самоиндукции на протекание тока в цепи очень наглядно демонстрируется характером изменения тока в цепи, содержащей индуктивность и активное сопротивление при ее подключении и отключении от источника тока. В положении переключателя, показанном на рисунке, в цепи идет ток

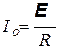. (20.16)

Предположим, что в некоторый момент времени переключатель мгновенно отключает источник тока и замыкает индуктивность на резистор. В отсутствие источника сила тока в цепи начнет убывать, но возникнет ЭДС самоиндукции, которая будет ее поддерживать. Падение напряжения на резисторе должно быть равно ЭДС самоиндукции :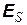

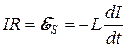. (20.17)

Разделим на :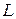

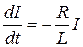(20.18)

Разделим в (20.17) переменные:

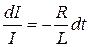(20.19)

После интегрирования получаем:

. (20.20)

Потенцирование этого соотношения дает зависимость тока от времени:

. (20.21)

При ток равен начальному значению 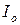, поэтому и константа равна этому току:

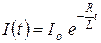. (20.22)

Графически эта зависимость выглядит так, как это показано на рисунке. Решение аналогичного уравнения для нарастания тока в цепи приводит к соотношению

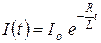. (20.23)

Явление взаимной индукции

Как и самоиндукция, явление взаимной индукции является частным случаем явления электромагнитной индукции. Заключается оно в том, что если один контур создает в пространстве магнитное поле, в котором находится другой контур, то при изменениях тока в первом контуре во втором возникает ЭДС индукции (ЭДС взаимоиндукции) 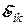, которая противодействует изменению магнитного потока в первом контуре.

Допустим, что имеются два контура, расположенные недалеко друг от друга, так что магнитные поля, создаваемые каждым из них, создают через витки другого контура ощутимый магнитный поток. Обозначим магнитный поток, создаваемый первым контуром с током 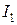через поверхности витков второго контура равен . Этот поток, очевидно пропорционален силе тока в первом контуре:

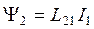. (20.24)

Аналогичным образом ток второго контура создает через витки первого поток

. (20.25)

Контуры в этом в этом случае называют связанными. При изменениях тока в одном из контуров в другом индуцируется ЭДС взаимной индукции соответственно

и . (20.26)

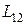Коэффициенты и называют коэффициентами взаимной индукции или взаимными индуктивностями. Их величина определяется формой, размерами, взаимным расположением контуров и магнитными свойствами окружающей среды. В отсутствие ферромагнетиков эти коэффициенты одинаковы.

Энергия магнитного поля

В цепи, показанной на рисунке, в исходном состоянии течет ток по индуктивности 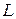и резистору 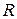. При отключении источника тока магнитный поток в индуктивности должен упасть до нуля, но ЭДС самоиндукции некоторое время поддерживает ток, препятствуя его прекращению. При этом в резисторе продолжает выделяться энергия. В схеме и окружающих телах никаких изменений, кроме уменьшения индукции магнитного поля в катушке индуктивности не происходит. Остается предположить, что выделяющаяся в резисторе энергия была связана с существованием магнитного поля в катушке.

В процессе уменьшения тока за время 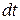ЭДС самоиндукции 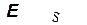совершает работу

. (20.27)

Если индуктивность катушки остается постоянной, то 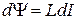и

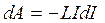. (20.28)

Ток в индуктивности спадает от некоторого значения I до нуля, поэтому вся работа за время исчезновения тока

. (20.29)

Именно такой энергией обладает магнитное поле катушки при прохождении по ней тока:

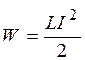. (20.30)

Для идеального соленоида (катушки) 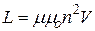, произведение 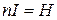дает напряженность поля соленоида, поэтому

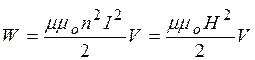. (20.31)

Поле идеального соленоида сосредоточено внутри соленоида, поэтому можно утверждать, что с магнитным полем связана энергия, распределенная в пространстве с плотностью

. (20.32)

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: