Напряженность магнитного поля

Ротор результирующего поля в магнетике

. (19.3)

Учтем, что ротор внешнего поля определяется плотностью макроскопического тока . Аналогичное соотношение справедливо и для поля создаваемого магнетиком:

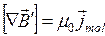. (19.3)

где - плотность молекулярных токов.

Аналогично тому, как для описания электриРческого поля в диэлектриках ис­пользуется вспомогательная величина – вектор электрической индукции , для описания магнитного поля в магне­тиках используется напряженность электрического поля . Чтобы сфор­мулировать ее определение необхо­димо выразить плотность молеку­лярных токов через вектор намагни­ченности . С этой целью найдем по­ток плотности молекулярных токов через неко­торую поверхность , опирающуюся на контур (рисунок 19.1). При этом необходимо учесть, что поток соз­дают только токи, нанизанные на контур . Другие токи либо не пересекают поверхность вовсе, либо пересекают ее дважды в противоположных направлениях, и потока создать не могут.

На элемент контура нанизываются те токи, центры которых попадают внутрь косого цилиндра с высотой и основанием, равным площади молекулярного тока . Объем такого цилиндра равен . Если концентрация молекулярных токов 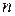, то в этот объем попадают токи

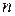
(19.4)

токов, и суммарный поток, создаваемый ими равен:

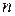
, (19.5)

где - сила молекулярного тока.

Теперь необходимо учесть, что произведение – магнитному моменту молекулярного тока. А его произведение на концентрацию дает магнитный момент единицы объема, т.е. модуль вектора намагниченности. Поэтому поток, создаваемый молекулярными токами, нанизанными на элемент контура, оказывается равным:

(19.6)

Соответственно поток плотности молекулярных токов через всю поверхность оказывается равным циркуляции вектора намагниченности по контуру :

(19.7)

По теореме Стокса

, (19.8)

а значит

. (19.9)

Таким образом,

. (19.10)

Теперь приходим к следующему соотношению для ротора результирующего поля в магнетике Объединим роторы

. (19.11)

 

Объединим роторы в (19.11) и получим, что

. (19.12)

 

Ротор величины, в круглых скобках в (19.12) определяется плотностью только макроскопических токов, и ее, по определению, называют напряженностью магнитного поля:

. (19.13)

 

Теорема о циркуляции вектора напряженности магнитного поля

Теоремой о циркуляции называют интегральное соотношение, являющееся следствием формулы (19.12). В соответствии с определением (19.13)

. (19.14)

Поток через некоторую поверхность , опирающуюся на контур ,в соответствии с теоремой Стокса, представляется в виде:

. (19.15)

Интеграл в правой части соотношения (19.15) представляет собой общий ток через поверхность . Для токов, протекающих по проводам, его следует заменить на алгебраическую сумму токов в проводах, пересекающих поверхность: . Это есть те проводники, которые охватываются контуром . Поэтому можно утверждать, что

. (19.16)

Это соотношение и называют теоремой о циркуляции вектора напряженности электрического поля.

 

Магнитная проницаемость

Для характеристики магнитных свойств среды используется параметр , который называют магнитной восприимчивостью (аналогичный диэлектрической восприимчивости 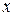в соотношении ). Традиционно намагниченность связывают с напряженностью магнитного поля:

. (19.17)

Для большинства веществ в не очень сильных полях магнитная восприимчивость является характерной для данного вещества безразмерной константой. Часто используется молярная восприимчивость , равная произведению на молярный объем вещества: .

Подставим значение намагниченности из (19.17) в (19.13):

. (19.18)

Выразим напряженность поля из (19.18):

. (19.19)

Величину обозначают 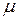и называют относительной магнитной проницаемостью:

. (19.20)

Тогда соотношение (19.19) приводится к виду:

, (19.21)

И можно утверждать, что напряженность магнитного поля есть вектор, направленный также, как индукция, но в раз меньший. Однако необходимо иметь в виду, что это утверждение перестает быть справедливым в анизотропных средах.

Виды магнетиков.

Традиционно по величине магнитной восприимчивости (и соответственно магнитной проницаемости) вещества делят на три группы диамагнетики, парамагнетики и ферромагнетики.

У диамагнетиков отрицательна (!) и по модулю составляет порядка . Это означает, что вектор намагниченности в них направлен навстречу напряженности внешнего поля.

У парамагнетиков положительна и имеет значение порядка .

У ферромагнетиков достигает значений порядка . Кроме того ферромагнетики имеют еще ряд особенностей, которые мы рассмотрим позднее. Необходимо отметить, что при повышении температуры ферромагнетики изменяют свои свойства и при характерной для каждого вещества критической температуре переходят в парамагнитное состояние, т.е. становятся парамагнетиками. Можно считать ферромагнетики частным случаем парамагнетиков, которые при понижении температуры испытывают фазовый переход в ферромагнитное состояние.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: