 |
Вихревое электрическое поле
|
|
|
|
Говоря о природе ЭДС индукции, мы связали ее возникновение с действием силы Лоренца на заряды в движущемся проводнике. Однако для покоящегося контура, расположенного в изменяющемся магнитном поле, такое объяснение является неприемлемым. Тем не менее, ЭДС индукции возникает!
Возникновение индукционного тока в замкнутом контуре при изменении магнитного потока, связанном с изменением внешнего поля обусловлено действием неких сторонних сил, которые не связаны ни с химическими превращениями в контуре, ни с магнитными силами. Поэтому будем считать, что в рассматриваемом случае ток в контуре возникает за счет действия электрического поля с напряженностью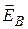 
. В замкнутом контуре циркуляция этого поля дает величину ЭДС индукции:
. (20.33)
Поскольку 
, можно утверждать, что
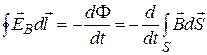. (20.34)
Поскольку рассматриваемый контур предполагается неподвижным, дифференцирование по времени можно поменять местами:
. (20.35)
По теореме Стокса
. (20.36)
Поэтому
. (20.37)
Поверхность интегрирования произвольна, поэтому должны быть равны подынтегральные выражения:
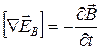. (20.38)
Итак, ротор поля 
оказался не равным нулю, в отличие от электростатического поля. Поэтому называют вихревым электрическим полем.
Одна из важнейших идей Максвелла заключалась в том, что он предположил, что изменяющееся во времени магнитное поле создает в окружающем пространстве вихревое электрическое поле независимо от наличия в данной точке пространства проводящего контура. Контур, точнее протекание в нем индукционного тока, является только индикатором наличия вихревого электрического поля.
Наконец, отметим, что поскольку ротор электростатического поля всегда равен нулю, можно утверждать что всегда
|
|
|
. (20.39)
Понятие о токе смещения
Для не изменяющегося во времени (стационарного) магнитного поля ротор вектора напряженности равен вектору плотности макроскопического тока:
. (20.40)
Возьмем дивергенцию от обеих частей этого соотношения:
. (20.41)
С одной стороны, дивергенция ротора всегда равна нулю, с другой - дивергенция вектора плотности тока может быть не равна нулю: в соответствии с уравнением непрерывности
. (20.42)
Уравнение непрерывности указывает на то, что при нестационарных процессах дивергенция плотности тока может отличаться от нуля. Например, при разряде конденсатора на резистор уменьшающийся заряда на конденсаторе является источником линий вектора плотности тока.
Максвелл предположил, что в правой части уравнения (20.40) () в действительности присутствует еще одно слагаемое, т.е. уравнение имеет вид:
. (20.43)
Дополнительное слагаемое он назвал плотностью тока смещения.
Определяющим свойством плотности тока смещения является условие.
. (20.44)
Этим обеспечивается выполнение равенства (20.41).
Из уравнения непрерывности следует, что
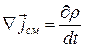. (20.45)
Плотность заряда связана с электрической индукцией (электрическим смещением) соотношением:
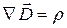. (20.46)
Продифференцируем это соотношение по времени и поменяем порядок дифференцирования по времени и координатам:
. (20.47)
Тогда
. (20.48)
Тогда можно утверждать, что
. (20.49)
Соответственно ротор напряженности магнитного поля
. (20.50)
Это уравнение является одним из основных в теории электромагнитного поля.
Таким образом, ток смещения по существу представляет собой фактически изменяющееся во времени электрическое поле. Из всех свойств, присущих собственно электрическому току, для тока смещения характерна только одно - способность создавать магнитное поле. Ток смещения присутствует и в обычных проводниках, если в них имеется изменяющееся во времени электрическое поле. Однако в проводниках его плотность пренебрежимо мала по сравнению с плотностью обычного тока.
|
|
|
Уравнения Максвелла
С использованием представления о токе смещения Максвелл разработал единую теорию электрических и магнитных явлений, которая объясняла все имевшиеся экспериментальные факты и предсказала существование новых явлений, в частности, электромагнитных волн.
В основе теории лежит система уравнения, которую называют уравнения Максвелла.
Первая пара:
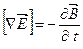(17); 
(18)
(17) связывает 
при наличии изменяющегося во времени 
. Фактически оно выражает закон электромагнитной индукции.
(18) математически выражает тот факт, что у магнитного поля нет источников – магнитных зарядов.
Вторая пара:
(19); 
(20)
(19) отражает тот факт, что магнитное поле порождается током проводимости и током смещения (переменным электрическим полем).
(20) отражает тот факт, что у электрического поля имеются источники – электрические заряды.
В первую пару входят основные характеристики полей - и 
; во вторую – вспомогательные. Это уравнения в дифференциальной форме
Каждое из уравнений (17) и (19) является векторным, т.е. в них заключены по три скалярных уравнения. Всего в систему входит 8 уравнений, а функций – 12 (по три ….)
|
|
|
