 |
Методические указания.
|
|
|
|
Задание выполняется на чертеже, сделанном при выполнении задания 1. Изучив теоретические пояснения к заданию 2, найдите и укажите на чертеже рекомендуемую точку размещения склада.
Основой выполнения задания 2 является изучение метода определения оптимального места размещения распределительного склада в случае прямоугольной конфигурации сети автомобильных дорог ("метод пробной точки").
Сначала на примере отдельного участка транспортной сети разберем суть метода.
Пусть на участке дороги длиной 30 км (участок AD на рис.5) имеется четыре потребителя материального потока: А, В, С и D. Месячный грузооборот каждого из них указан в скобках. Оптимальное место расположения распределительного склада легко oпределить методом, который можно назвать "метод пробной точки ")(ссылка на Гаджинского, стр 95).
 |
Рис. 5. Определение оптимального места расположения распределительного склада на участке обслуживания
Суть метода состоит в последовательной проверке каждого отрезка обслуживаемого участка.
Введем понятие пробной точки отрезка, а также понятия левого и правого грузооборотов пробной точки.
Пробной точкой отрезка назовем любую точку, находящуюся на этом отрезке и не принадлежащую его концам (т. е. пробная точка не совпадает с точками А, В, С и D).
Левый грузооборот пробной точки — грузооборот потребителей, расположенных на всем участке обслуживания слева от пробной точки.
Правый грузооборот пробной точки — грузооборот потребителей, расположенных справа.
Участок обслуживания проверяют с крайнего левого конца. Сначала анализируют первый отрезок участка (в нашем случае — отрезок АВ). На данном отрезке ставится пробная точка и подсчитывается сумма грузооборотов потребителей, находящихся слева и справа от поставленной точки. Если грузооборот потребителей, находящихся справа, больше, то проверяется следующий отрезок. Если меньше, то принимается решение о размещении склада в начале анализируемого отрезка.
|
|
|
Проверка пробных точек продолжается до тех пор, пока не появится точка, для которой сумма грузооборотов потребителей с левой стороны не превысит сумму грузооборотов потребителей с правой стороны. Решение принимается о размещении склада в начале этого отрезка, т. е. слева от пробной точки. В нашем примере — это точка С.
Рассмотрим вариант, когда сумма грузооборотов слева и справа от пробной точки очередного отрезка становится одинаковой. Начало этого отрезка (точка М, рис.6) является первым, а конец (точка N) последним из возможных мест расположения распределительного склада на участке обслуживания. Распределительный центр может быть расположен в любой из точек отрезка MN участка обслуживания.
 |
Рис. 6. Определение оптимального расположения распределительного склада при равенстве «левого» и «правого» грузооборота пробной точки
Для определения методом пробной точки оптимального узла прямоугольной транспортной сети (для размещения распределительного склада) следует нанести на карту района координатные оси, сориентированные параллельно дорогам. Определив координаты потребителей, необходимо на каждой координатной оси найти методом пробной точки оптимальное место расположения координаты X и координаты Y искомого узла.
В качестве примера рассмотрим обслуживаемую систему, состоящую из четырех потребителей (рис.7). Сеть дорог — прямоугольная. Присваивая ординатам и абсциссам потребителей соответствующие значения грузооборота, найдем методом пробной точки ординату и абсциссу оптимального узла транспортной сети. Размещение распределительного склада в найденном узле (точка О) обеспечит минимальный грузооборот по доставке товаров со складов
|
|
|
 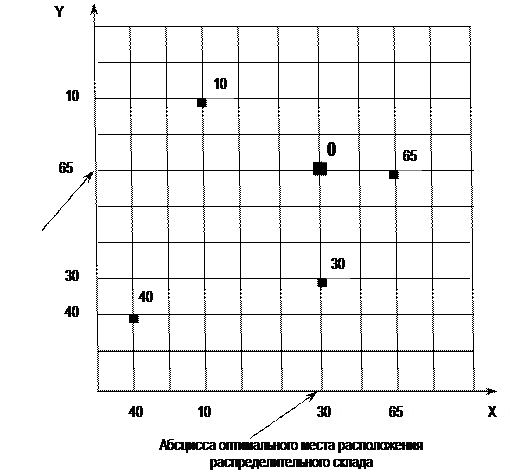 |
Рис. 7. Определение оптимального места расположения распределительного склада в условиях прямоугольной сети автомобильных дорог (точками на схеме обозначены потребители материального потока, числами – грузооборот потребителей, т \ мес.)
Задание 3. Методом частичного перебора найти узел транспортной сети, рекомендуемый для размещения склада, снабжающего магазины.
На территории района (рис.3) имеется восемь магазинов, торгующих продовольственными товарами.
|
|
|


