 |
Гидростатическое давление.
|
|
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ИЖЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
ЧАЙКОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (филиал)ИжГТУ
КАФЕДРА АВТОМОБИЛЬНОГО ТРАНСПОРТА
Е.П. Филиппова
ПРИМЕРЫ ЗАДАЧ ПО ГИДРАВЛИКЕ
Практическое пособие
и задания для контрольных работ
студентам – заочникам по специальности
«Промышленное и гражданское строительство»
Издание ЧТИ ИжГТУ 2007 г.
ПРИМЕРЫ ЗАДАЧ ПО ГИДРАВЛИКЕ
Практическое пособие
и задания для контрольных работ
студентам – заочникам по специальности
«Промышленное и гражданское строительство»
Составитель: ст. преподаватель Е.П.Филиппова;
2007 г.
ã Е.П. Филиппова
Утверждено на заседании кафедры «Автомобильный транспорт» Чайковского технологического института (филиала) ИжГТУ, протокол №
Электронная версия в Word 2000 находится в
Чайковском технологическом институте (филиале) ИжГТУ
Настоящее пособие предназначено для студентов специальности «Промышленное и гражданское строительство» очно – заочной и заочной форм обучения, выполняющих контрольную работу по общему курсу гидравлики.
В пособии приведены краткие теоретические сведения, термины, определения, расчетные зависимости и методические указания для решения задач по основным темам гидростатики и гидродинамики, расчету трубопроводных систем, приведены примеры решения основных типов гидравлических задач и задания для выполнения контрольной работы.
| СОДЕРЖАНИЕ | Стр | ||
| ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ……………………………… | |||
| Раздел 1. ГИДРОСТАТИКА ……………………………………. | |||
| Тема 1.1. Физические свойства жидкостей. Гидростатическое давление …………………… | |||
| Тема 1.2. Сила гидростатического давления на плоские поверхности………………………………………. | |||
| Тема 1.3. Давление на криволинейные поверхности……… | |||
| Тема 1.4. Равновесие тел, погруженных в жидкость……... | |||
| Тема 1.5. Относительный покой жидкости ………………….. | |||
| Раздел 2. ОСНОВЫ ГИДРОДИНАМИКИ | |||
| Тема 2.1. Гидравлические характеристики потока……….. | |||
| Тема 2.2. Уравнение Бернулли для идеальной жидкости… | |||
| Тема 2.3: Уравнение Бернулли для реальной жидкости. Гидравлические сопротивления………………... | |||
| Тема 2.4. Истечение жидкости через отверстия и насадки. | |||
| Тема 2.5. Гидравлический расчет напорных трубопроводов | |||
| Тема 2.6. Безнапорное движение жидкости ………………. | |||
| Раздел 3. ГИДРАВЛИЧЕСКИЕ МАШИНЫ | |||
| Литература…………………………………………………………………. | |||
| ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ…………………………………. | |||
| ВАРИАНТЫ ЗАДАНИЙ…………………………………………………… |
ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ.
|
|
|
Гидравлика или техническая механика жидкостей – прикладная часть механики жидкостей и газов, изучающая законы равновесия и движения жидкостей с целью практического применения.
Гидростатика – раздел гидравлики, изучающий жидкость, находящуюся в покое, относительном покое и равновесие тел, погруженных в жидкость.
Гидродинамика – раздел гидравлики, изучающий законы движения жидкостей.
Жидкость – любая среда, обладающая свойством текучести. Различают малосжимаемые жидкости (капельные) и сжимаемые (газообразные). Законы равновесия и движения капельных жидкостей применимы, в основном, и к газам.
|
|
|
Идеальная жидкость -идеальная модель реальной жидкости, используемая для установления базовых законов гидравлики. Идеальная жидкость характеризуется:
- абсолютной неизменяемостью объема (несжимаемостью);
- полным отсутствием вязкости (сил трения).
Идеальный газ – идеальная модель газа, характеризующаяся полным отсутствием взаимодействия между молекулами газа.
Нормальные условия – стандартные значения давления и температуры, используемые при расчетах в качестве базовых:
РО = 0,1013 МПа, tО = 20 оС – для жидкостей, tО = 0 оС – для газов.
Силы, действующие на жидкость, подразделяются:
Внутренние – силы взаимодействия между частицами жидкости;
Внешние – силы, приложенные со стороны (в том числе со стороны жидкости, окружающей рассматриваемый объем).
Внешние силы делятся:
1) Массовые (или объемные). К ним относятся: собственный вес жидкости, силы инерции;
2) Поверхностные силы - приложенные к поверхности, ограничивающей рассматриваемый объем: сила атмосферного давления, сила избыточного давления, силы трения, реактивная сила (реакция поверхности).
На жидкость, находящуюся в покое, не воздействуют силы трения и силы инерции.
Жидкостный манометр – тонкая трубка для измерения давления соответствующей высотой столба жидкости с данной плотностью.
Пьезометр – стеклянная трубка для измерения давления жидкости высотой столба воды. Различают:
- открытый пьезометр – с открытым верхним концом. Производит измерение избыточного (манометрического) давления;
- закрытый пьезометр – вакуумная трубка. Производит измерение абсолютного давления (с учетом атмосферного).
РАЗДЕЛ 1. ГИДРОСТАТИКА.
ТЕМА 1.1. ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТИ.
ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ.
Физические свойства жидкостей, используемые в гидравлических расчетах:
Плотность r, кг/м3 - отношение массы однородной жидкости (М) к занимаемому объему (V):
(1.1.1)
Удельный объем – величина, обратная плотности: m = 1/r.
Плотность капельной жидкости зависит, в основном, от температуры:
ПЛОТНОСТЬ ПРЕСНОЙ ВОДЫ
Таблица 1
| t, °С | r, кг/м3 | t, °С | r, кг/м3 | t, °С | r, кг/м3 | t, °С | r, кг/м3 |
| 999,87 | 999,73 | 998,65 | 992,24 | ||||
| 1000,0 | 999,55 | 998.23 | 983,24 | ||||
| 999,97 | 999,30 | 997,12 | 971,83 | ||||
| 999,88 | 999,00 | 995,67 | 958,38 |
Плотность газов зависит от температуры и давления:
|
|
|
ПЛОТНОСТЬ СУХОГО ВОЗДУХА ПРИ Р = 0,1 мПа
Таблица 2
| t, °С | r, кг/м3 | t, °С | r, кг/м3 | t, °С | r, кг/м3 | t, °С | r, кг/м3 |
| -20 | 1.35 | 1,17 | 1,06 | 0,97 | |||
| 1,25 | 1,13 | 1,03 | 0,94 | ||||
| 1,21 | 1,10 | 1,00 | 0,92 |
Сжимаемост ь - относительное изменение объема жидкости V на величину DV при равномерном всестороннем сжатии данного объема на величину DР.
Сжимаемость характеризуется коэффициентом объемного сжатия:
, Па –1 (1.1.2)
Коэффициент объемного сжатия есть величина, обратная модулю объемной упругости:
Е = 1/ bV, Па. (1.1.3)
Температурное расширение - относительное увеличение объема жидкости V на величину DV, соответствующую приращению температуры на величину DТ.
Расширение характеризуется коэффициентом температурного расширения:
,0С-1 (1.1.4)
Средняя величина коэффициента bt для капельных жидкостей в интервале температур от t1 до t2 определяется:
(1.1.5)
Вязкость – свойство жидкости при движении сопротивляться сдвигающим усилиям, возникающее за счет трения на поверхностях соприкосновения жидких слоев друг с другом,
Вязкость характеризует степень текучести и выражается через динамический и кинематический коэффициенты вязкости.
Динамическая (абсолютная) вязкость (m) выражает силу внутреннего трения на единицу площади соприкасающихся слоев жидкости.
Сила трения пропорциональна изменению скорости по сечению потока (градиенту скорости du/dy), площади соприкосновения слоев S и динамической вязкости: 
(1.1.6)
Единица измерения динамической вязкости паскаль – секунда (Па . с).
Кинематическая вязкость (n) - отношение динамической вязкости к плотности жидкости – 
, м2/с. (1.1.7)
В справочной литературе значение n часто приводится в стоксах (Ст):
1 Ст = 1 см2/с =10-4 м2 /с.
Для капельных жидкостей вязкость зависит от температуры и практически не зависит от давления.
КИНЕМАТИЧЕСКАЯ ВЯЗКОСТЬ ВОДЫ n, 106 м2/с
Таблица 3
| t, °С | ||||||||
| n | 1,79 | 1,67 | 1,47 | 1,39 | 1,31 | 1,24 | 1,18 | 1,12 |
| t, °С | ||||||||
| n | 1,06 | 1,01 | 0,90 | 0,80 | 0,72 | 0,65 | 0,60 | 0,55 |
| t, °С | ||||||||
| n | 0,48 | 0,45 | 0,42 | 0,39 | 0,37 | 0,35 | 0,33 | 0,30 |
|
|
|
Для газов кинематическая вязкость возрастает с увеличением температуры и уменьшается с увеличением давления.
Для совершенных газов (к которым можно отнести реальные двухатомные газы и их смеси) взаимосвязь между плотностью, давлением и температурой газа массой m = 1 кг выражается уравнением Клапейрона:
РV = RТ или 
(1.1.8)
где Р – абсолютное давление, Па;
R- удельная газовая постоянная, Дж/ кг .К;
Т – абсолютная температура, К.
На практике вязкость измеряется вискозиметрами и часто выражается в условных градусах Энглера (оЕ). Для перехода к кинематической вязкости служит эмпирическая формула Убеллоде:
n = (0,0731 оЕ – 0,0631 / оЕ) 10-4, м2 /с (1.1.9)
Испаряемость жидкости характеризуется давлением насыщенных паров. Давление насыщенных паров (РН.П) – давление паров жидкости, насыщающих пространство над свободной поверхностью.
Поверхностное натяжение жидкости обусловлено силами молекулярного притяжения поверхностного слоя жидкости, стремящимися сократить свободную поверхность. По сравнению с давлением на плоской поверхности, давление на выпуклой поверхности (в несмачиваемой капиллярной трубке) увеличивается, а на вогнутой (смачиваемой) уменьшается на величину, определяемую по формуле Лапласа:
РПОВ = s [ (1/r1) + (1/r2)] (1.1.10)
где s - поверхностное натяжение, Н/м;
r1, r2 – главные радиусы кривизны.
Поверхностное натяжение зависит от температуры:
s = sо - b Dt (1.1.11)
где sо – поверхностное натяжение при соприкосновении с воздухом при температуре 0 оС. Для воды sо = 0,076 Н/м, b = 0,00015 Н/ м . оС.
Формула (1.10) для определения увеличения давления в капиллярных трубках принимает вид:
РПОВ = 2s / r или hКАП = 2 s / r g r (1.1.12)
где r – радиус трубки (капилляра);
hКАП – высота капиллярного поднятия, соответствующая давлению РПОВ.
Данные о физических свойствах жидкостей и газов приводятся в справочной литературе. Некоторые справочные данные приводятся в качестве примера в таблицах 1…3 данного пособия.
Гидростатическое давление, Р -сила, действующая на точку в неподвижной жидкости.
Единицы измерения давления:
Основная единица измерения давления в системе СИ - Паскаль (Па).
1Па = 1 Н/м2, 1кПа = 103 Па (килопаскаль), 1мПа = 106 Па (мегапаскаль).
Внесистемные единицы:
1) Высота столба жидкости с плотностью r: h = Р / r g.
При нормальных условиях
1 мм вод.ст. = 9,806 Па
1 мм рт. ст. = 133,322 Па.
2) Атмосфера: 1 атм = 760 мм рт. ст. = 101325 Па. 1 ати - избыточное давление, выраженное в атмосферах.
|
|
|
3) При больших значениях давления и приближенных расчетах используются соотношения:
1атм =105 Па = 0,1 МПа = 10 м вод.ст. = 1 кг/см2
Величина вакуума дополнительно измеряется:
- долями атмосферы, если считать атмосферу за 1;
- в %, если считать 1 атмосферу за 100%.
Гидростатическое давление обладает двумя основными свойствами:
1) всегда направлено по нормали к поверхности, на которую действует и направлено внутрь объема (является сжимающим);
2) при изменении ориентации (угла наклона) поверхности величина давления в точке, относительно которой происходит поворот, не изменяется;
Поверхность равного давления - поверхность, на которой все точки находятся под одинаковым давлением.
Абсолютное (полное) гидростатическое давление РА в любой точке объема определяется по основному уравнению гидростатики:
РА = РО + r g h, Па (1.1.13)
где РО – поверхностное давление (на свободной поверхности или на какой – либо поверхности равного давления), Па;
r g h - весовое давление, Па;
r - плотность жидкости, кг/ м3;
g – ускорение свободного падения, g = 9,81 м/сек2;
h – заглубление точки от поверхности с давлением РО, м;
Из формулы (1.1.13) следует: давление, приложенное к поверхности, передается без изменения всем точкам внутри данного объема (закон Паскаля).
Если РО = Ра (атмосферное давление), то уравнение (1.1.13) принимает вид: РА = Ра + r g h. (1.1.14)
Избыточное давление Р - разность между абсолютным и атмосферным давлением при РА > Ра:
В общем случае: Р = РА – Ра = (РО + r g h) - Ра (1.1.15)
Пьезометрическая высота - высота столба жидкости, соответствующая избыточному давлению (измеряется открытым пьезометром):
hИЗБ = 
(1.1.16)
При РО = Ра избыточное давление равно весовому давлению
Р = r g h (1.1.17)
и пьезометрическая высота равна высоте жидкости в сосуде
hИЗБ = h = Р / r g (1.1.18)
Вакуум, РВАК - разность между абсолютным и атмосферным давлением при
РА < Ра :
РА - Ра = РВАК = r g hВАК и hВАК = РВАК / r g (1.1.19)
Потенциальный напор (напор), Н: -потенциальная энергия Е, принадлежащая единице веса жидкости. Потенциальная энергия покоящейся жидкости (полная возможная работа) состоит из суммы двух видов энергии:
1) потенциальной энергии положения Z;
2) потенциальной энергии давления Р.
H = Z + Р/r g = Z + hИЗБ, м (1.1.20)
где Z - геометрический напор (превышение над плоскостью отсчета); м;
hИЗБ - напор давления, м.
Для всех точек данного объема покоящейся жидкости величина потенциального напора постоянна (H = const) и определяется превышением уровня жидкости в пьезометре над плоскостью отсчета.
В случае открытых сосудов напор определяется превышением свободной поверхности жидкости над плоскостью сравнения.
Гидростатическое давление в газах.
В случае однородной атмосферы (r = const) распределение давления в газе не отличается от капельных жидкостей (1.1.1).
Любая горизонтальная поверхность, проведенная внутри объема, будет поверхностью равного давления.
При изотермическом изменении состояния газа (Т= const) давление будет уменьшаться с увеличением высоты.
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
При решении задач на тему гидростатического давления необходимо различать и не смешивать понятия абсолютного давления РА, избыточного давления Р, вакуума РВАК, знать взаимосвязь между давлением (Па) и соответствующей ей пьезометрической высотой (h), уяснить понятие напора, знать закон Паскаля и свойства гидростатического давления.
При определении давления в точке объема или на точку площадки используется основное уравнение гидростатики (1.1.13).
При решении задач с системой сосудов необходимо составить уравнение абсолютных давлений, обеспечивающих неподвижность системы, т.е. равенства нулю алгебраической суммы всех действующих давлений. Уравнение составляется для какой - либо поверхности равного давления, выбранной в качестве поверхности отсчета.
Все единицы измерения величин следует принимать в системе СИ: масса – кг; сила – Н; давление – Па; линейные размеры, площади, объемы – м, м2, м3.
ПРИМЕРЫ
Пример 1.1.1. Определить изменение плотности воды при ее нагревании от t1= 7оС до t2 = 97оС, если коэффициент температурного расширения bt =0,0004 оС-1.
Решение. При нагревании удельный объем воды увеличивается от V1 до V2.
По формуле (1.1.1) плотность воды при начальной и конечной температурах составляет:
r1 = М / V1, r2 = М / V2.
Так как масса воды постоянна, то изменение плотности выражается:
Из формулы (1.4) увеличение объема воды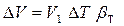 
, тогда
Примечание: изменение плотности жидкости при сжатии определяется аналогично с использованием коэффициента объемного сжатия по формуле (1.1.2). При этом V2 = V1 - DV.
Пример 1.1.2. Определить объем расширительного бачка системы водяного охлаждения вместимостью 10 литров при нагревании от температуры t1 = 15оС до t2 = 95оС при давлении, близком к атмосферному.
Решение. Без учета коэффициента запаса объем бачка равен дополнительному объему воды при температурном расширении. Из формулы (1.1.4) увеличение объема воды
.
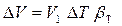Плотности воды принимаем по таблице 1: r1 = 998,9 кг/м3, r2 = 961,8 кг/ м3. Коэффициент температурного расширения определяем по формуле (1.1.5):
Первоначальный объем V =10л = 10 .10-3 м3 = 0,01 м3.
Дополнительный объем воды:
DV = 10 .10-3 (95 -15) 0,46 .10-3 = 368 .10-6 м3 = 0,368 л
Пример 1.1.3. В охлаждаемом сосуде газ, имеющий первоначальное давление Р1 = 105 Па. и занимающий объем V1 = 0,001 м3, сжимается до давления Р2 = 0,5 . 106 Па. Определить объем газа после сжатия.
Решение. В случае охлаждаемого сосуда процесс является изотермическим (t = const) при котором уравнение состояния газа (1.1.8) принимает вид:
Р V = const или Р1 V1 = Р2 V2
Откуда определяем объем газа после сжатия
V2= Р1 V1 / Р2 = 1 . 105 . 0.001 / 0,5 . 106 = 0,0002 м3 =0,2 л.
Пример 1.1.4. Определить объем воды, который необходимо дополнительно подать в трубопровод диаметром d = 500 мм и длиной L = 1км, заполненный водой перед гидравлическим испытанием при атмосферном давлении и температуре t = 20оС, для повышения давления в нем на DР = 5 .106 Па. Материал труб считать абсолютно жестким.
Решение. Для определения дополнительного объема воды, который необходимо подать используем соотношение (1.1.2):
= 
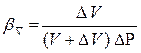
Первоначальный объем воды в трубопроводе равен объему трубопровода:
Приняв по справочным данным модуль объемной упругости воды
Е = 2 . 109 Па, определяем коэффициент объемного сжатия:
bV = 1 /Е = 1 / 2 . 109 = 5 . 10-10, Па-1
Преобразовывая соотношение (1.1.2) относительно DV, получаем:
bV DР VТР + bV DР DV = DV; bV DР VТР = (1 + bV DР) DV
Выражая DV, получаем искомый дополнительный объем:
Пример 1.1.5. Определить среднюю толщину отложений dОТЛ в трубопроводе внутренним диаметром d = 0,3 м и длиной L = 2 км, если при выпуске воды в количестве DV =0,05 м3 давление в нем падает на величину DР = 1 . 106 Па.
Решение. Взаимозависимость изменения объема и давления воды характеризуется модулем объемной упругости.
Принимаем: Е = 2.109 Па.
Из формул (1.1.2) и (1.1.3) находим объем воды в трубопроводе с отложениями:
Этот же объем равен вместимости трубопровода:
Откуда определяем средний внутренний диаметр трубы с отложениями
Средняя толщина отложений составляет:
Пример 1.1.6. Вязкость нефти, определенная по вискозиметру Энглера, составляет 8,5оЕ. Вычислить динамическую вязкость нефти, если ее плотность r = 850 кг/м3.
Решение. По эмпирической формуле Убеллоде (1.1.9) находим кинематическую вязкость нефти:
n = (0,0731 оЕ – 0,0631 / оЕ) 10-4 =
= (0,0731 . 8,5 – 0.0631/8,5) = 0,614 . 10-4 м2/с
Динамическую вязкость находим из соотношения (1.1.7):
m = n r = 0,614 . 10-4 . 850 = 0,052 Па .с.
Пример 1.1.7. Определить высоту подъема воды в капиллярной трубке диаметром d = 0,001 м при температуре t = 80ОС.
Решение. По справочным данным находим:
плотность воды при температуре 80ОС r = 971,8 кг/м3;
поверхностное натяжение воды при температуре 20ОС sО = 0,0726 Н/м;
коэффициент b = 0,00015 Н/м ОС.
По формуле (1.1.11) находим поверхностное натяжение воды при температуре 80ОС:
s = sО - b Dt = 0,0726 – 0,00015 . (80 -20) = 0,0636 Н/м
По формуле (1.1.12) изменение поверхностного давления, определяющего высоту капиллярного поднятия hКАП, составляет:
РПОВ = 2s / r или r g hКАП = 2s / r,
откуда находим высоту подъема воды в трубке:
hКАП = 2 s / r g r = 2. 0,0636 / 971,8 . 9,81 . 0,0005 =
= 0,1272 / 4,768 = 0,027 м =2,7 см.
Пример 1.1.8. Определить абсолютное гидростатическое давление воды на дно открытого сосуда, наполненного водой. Глубина воды в сосуде h = 200 см. Атмосферное давление соответствует 755 мм рт. ст. Температура воды 20 оС. Выразить полученное значение давления высотой ртутного столба (rРТ = 13600 кг/м3) и водного столба.
Решение: По основному уравнению гидростатики для открытого резервуара абсолютное давление в любой точке объема определяется по формуле (1.1.14):
РА = Ра + r g h
По таблице 1 принимаем плотность воды при температуре 20 оС:
r = 998,23 кг/м3.
Переводя единицы измерения атмосферного давления и глубины воды в сосуде в систему СИ, определяем абсолютное давление на дне сосуда:
РА = 755 .133,322 + 998.23 . 9,81 . 2 =
= 100658 + 19585 = 120243 Па =120,2 КПа
Находим соответствующую высоту ртутного столба:
hА = Р/ rРТ g =120243 /13600 . 9,81 = 0, 902 м.
Находим высоту водного столба, соответствующую данному абсолютному давлению:
hА = РА / r g = 120243 / 998,23 . 9,81 = 12, 3 м.
Это означает, что если к уровню дна сосуда присоединить закрытый пьезометр (трубку, в которой создан абсолютный вакуум), то вода в нем поднимется на высоту 12,3 м. Давление этого столба воды уравновешивает абсолютное давление, оказываемое на дно сосуда жидкостью и атмосферным давлением.
Пример 1.1. 9. В закрытом резервуаре с водой давление на свободной поверхности РО =14,7 . 104 Па. На какую высоту Н поднимется вода в открытом пьезометре, присоединенном на глубине h = 5 м. Атмосферное давление соответствует hа = 10 м вод. ст.
Решение. Для решения данной задачи необходимо составить уравнение равенства абсолютных давлений со стороны резервуара и со стороны пьезометра относительно выбранной плоскости равного давления. Выберем плоскость равного давления 0-0 на уровне свободной поверхности в резервуаре.
Абсолютное давление со стороны резервуара на выбранном уровне равно поверхностному давлению:
РА = РО. (1)
Абсолютное давление на том же уровне со стороны жидкости в пьезометре складывается из атмосферного давления Ра и давления воды высотой h1:
РА = Ра + r g h1 (2)
Так как система находится в равновесии (покое), то абсолютные давления со стороны резервуара и со стороны пьезометра уравновешиваются. Приравнивая правые части равенств (1) и (2), получим:
РО = Ра + r g h1,
Величина атмосферного давления в системе СИ составляет:
Ра = 9,806 . 10 000 мм = 9,806 . 104 Па.
Находим высоту превышения уровня воды в пьезометре над выбранной плоскостью равного давления:
h1 = (РО - Ра) / r g = (14,7 . 104 - 9,806 . 104) /1000 . 9,81 = 5 м.
Это превышение не зависит от точки подключения пьезометра, так как давления столбов жидкости высотой h ниже плоскости сравнения слева и справа взаимно компенсируются.
Общая высота воды в пьезометре больше высоты h1 на глубину погружения точки присоединения пьезометра. Для данной задачи
Н = h1 + h = 5 + 5 = 10 м.
Примечание: аналогичный результат можно получить, выбрав в качестве плоскости равного давления уровень подключения пьезометра.
Пример 1.1.10. Построить эпюру абсолютного давления жидкости на ломаную стенку в открытом резервуаре.
Решение. Абсолютное давление в случае открытого резервуара определяется по формуле (1.1.14):
РА = Ра + r g h, т.е. избыточное давление в каждой точке увеличивается на величину поверхностного давления (закон Паскаля).
Избыточное давление определяется:
в т. С: Р = r g . 0 = 0
в т. В: Р = r g . Н2
в т. А: Р = r g (Н2 + Н1)
Отложим значение избыточного давления в точке В по нормали к стенке СВ и соединим с точкой С. Получим треугольник эпюры избыточного давления на стенку СВ. Для построения эпюры абсолютного давления в каждой точке необходимо добавить значение поверхностного давления (в данном случае атмосферного).
Аналогично ведется построение эпюры для отрезка АВ: Отложим значения избыточного давления в точке В и в точке А в направлении нормали к линии АВ, соединим полученные точки. Абсолютное давление получаем, увеличивая длину вектора на величину, соответствующую атмосферному давлению.
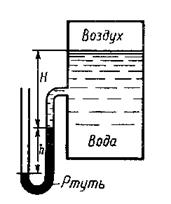Пример 1.1.11. Определить абсолютное давление воздуха в сосуде с водой, если показание ртутного манометра h = 368 мм, Н = 1 м, плотность ртути rРТ =13600 кг/м3. Атмосферное давление соответствует 736 мм рт.ст.
Решение.
Выберем свободную поверхность ртути в качестве поверхности равного давления. Атмосферное давление на поверхности ртути уравновешивается абсолютным давлением воздуха в сосуде РА, давлением столба воды высотой Н и столба ртути высотой h.
Составим уравнение равновесия и определим из него абсолютное давление воздуха (переводя все единицы в систему СИ):
Ра = РА + rВ g Н + rРТ g h, откуда
РА = Ра - rВ g Н - rРТ g h =
= 736 . 133,3 - 1000 . 9,81 . 1 - 13600 . 9,81 . 0,368 = 39202 Па
Так как абсолютное давление воздуха в сосуде меньше атмосферного, то в сосуде имеет место вакуум, равный разности атмосферного и абсолютного давлений:
РВАК = Ра – РА = 736 . 133,3 - 39202 = 58907 Па = 59 КПа.
Примечание: тот же результат можно получить, выбрав в качестве поверхности равного давления свободную поверхность воды в сосуде или поверхность раздела воды и ртути.
Пример 1.1.12. Определить избыточное давление РО воздуха в напорном баке по показаниям батарейного ртутного манометра. Соединительные трубки заполнены водой. Отметки уровней даны в м. Какой высоты должен быть пьезометр для измерения этого давления?
Решение. Избыточное давление РО = РА – Ра в баке уравновешивается давлением столбов ртути и воды в манометре.
Давления взаимно уравновешивающихся высот на участках изгиба манометра из рассмотрения исключаем. Суммируя (с учетом направления действия давления) показания манометра от открытого конца до уровня свободной поверхности, составим уравнение равновесия:
РО = rРТ g (1,8 – 0,8) - rВ g (1,6 – 0,8) +rРТ g (1,6 – 0,6) - rВ g (2,6 – 0,6) =
= rРТ g (1,8 – 0,8 +1,6 – 0,6) - rВ g (1,6 – 0,8 + 2,6 – 0,6) =
=13600 . 9,81 . 2 – 1000 . 9,81 . 2.8 = 239364 Па = 0,24 МПа
Из формулы (1.16) находим высоту столба воды, соответствующую избыточному давлению РО:
hИЗБ = РО / rВ g = 0,24 .106 / 1000. 9,81= 24,5 м
Высота пьезометра выше на величину превышения свободной поверхности воды в баке над плоскостью с нулевой отметкой:
Н = hИЗБ + 2,6 = 27,1 м.
Пример 1.13. Определить толщину s стальной стенки бака диаметром D = 4 м для хранения нефти (rН = 900 кг/м3) при высоте слоя нефти Н = 5 м. Давление на поверхности нефти РО = 24,5 . 104 Па. Допустимое напряжение на растяжение материала стенки s = 140 МПа.
Решение. Расчетная толщина стенки круглого бака (без коэффициента запаса) определяется из условия сопротивления максимальному избыточному давлению. Атмосферное давление в баке не учитывается, так как оно компенсируется атмосферным давлением с внешней стороны бака.
Максимальное избыточное давление Р стенка испытывает у дна:
Р = РА – Ра = РО + rН g Н - Ра =
= 24,5 . 104 + 900 . 9,81. 5 – 10 . 104 = 18,91 . 104 Па
Расчетная толщина стенки определяется по формуле:
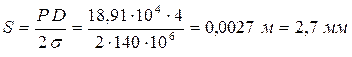
Пример 1.1.14. Определить перепад давлений воды в вертикальном трубном кольце, если в точке А она нагревается до температуры t1 = 95оС, а в точке В остывает до t2 = 70оС. Расстояние между центрами нагревания и охлаждения h1 = 12 м.
Решение. Перепад давлений обусловлен разностью гидростатических давлений столба горячей воды в левой трубе и остывшей воды в правой трубе.
Давления столбов воды высотой h2 в левой и правой трубах взаимно уравновешиваются и в расчете не учитываются, так как температура воды в них и, соответственно, плотность, одинаковы. Аналогично исключаем из расчета давления в левом и правом стояках высотой h3.
Тогда давление слева Р1 = rГ g h1, давление справа Р2 = rО g h1.
Перепад давлений составляет:
DР = Р2 – Р1 = rО g h1 - rГ g h1 = g h1 (rО - rГ)
Принимаем по справочным данным (таблица 1) плотности воды при температуре t1 = 95оС и t2 = 70оС: rГ = 962 кг/м3, rО = 978 кг/м3
Находим разность давлений
DР = g h1 (r2 - r1) = 9,81 . 12 (978 –962) = 1882 Па.
Пример 1.1.15. а) Определить избыточное давление воды в трубе, если РМАН = 0,025 МПа, Н1 = 0,5 м, Н2 = 3 м.
б)Определить показания манометра при том же давлении в трубе, если вся трубка заполнена водой, Н3 =5 м.
а)Решение. Избыточное давление в трубе уравновешено поверхностным давлением РО = РМАН в точке подключения манометра и системой столбов воды и воздуха в трубке. Давлением столбов воздуха можно пренебречь ввиду незначительности.
Составим уравнение равновесия с учетом направления давления столбов воды в трубке:
Р = РМАН + rВОД g Н2 - rВОД g Н1 =
= 0,025 + 1000 . 9,81. 10-6 (3 – 0,5) = 0,025 + 0,025 = 0,05 МПа
б) Решение. Уравнение равновесия для данного случая
Р = РМАН + rВОД g Н3,
откуда РМАН = Р - rВОД g Н3 = 0,05 - 1000. 9,81. 10-6 . 5 = 0,05 – 0,05 = 0 МПа.
|
|
|
