 |
Колебания груза на пружине
|
|
|
|
Рассмотрим колебания груза на пружине, при условии, что пружина не деформирована за пределы упругости. Покажем, что такой груз будет совершать гармонические колебания относительно положения равновесия (рис.1.1.3). Действительно, согласно закону Гука, сжатая или растянутая пружина создаёт гармоническую силу:
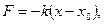
где 
– коэффициент жёсткости пружины, 
– координата положения равновесия, х – координата груза (материальной точки) в момент времени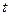 
, 
- смещение от положения равновесия.
Поместим начало отсчета координаты в положение равновесия системы. В этом случае 
.
Если пружину растянуть на величину х, после чего отпустить в момент времени t =0, то уравнение движения груза согласно второму закону Ньютона примет вид -kx =ma, или 
, и
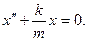(1.1.6)
Это уравнение совпадает по виду с уравнением движения (1.1.3) системы, совершающей гармонические колебания, его решение будем искать в виде:
. (1.1.7)
Подставим (1.17) в (1.1.6), имеем: 
то есть выражение (1.1.7) является решением уравнения (1.1.6) при условии, что 
Если в начальный момент времени положение груза было произвольным, то уравнение движения примет вид:
.
Рассмотрим, как меняется энергия груза, совершающего гармонические колебания в отсутствие внешних сил (рис.1.14). Если в момент времени t =0 грузу сообщить смещение х=А, то его полная энергия станет равной потенциальной энергии деформированной пружины 
, кинетическая энергия равна нулю (точка 1).
На груз действует сила F= -kx, стремящаяся вернуть его в положение равновесия, поэтому груз движется с ускорением и увеличивает свою скорость, а, следовательно, и кинетическую энергию. Эта сила сокращает смещение груза х, потенциальная энергия груза убывает, переходя в кинетическую. Система «груз - пружина» замкнутая, поэтому её полная энергия сохраняется, то есть:
|
|
|
. (1.1.8)
В момент времени 
груз находится в положении равновесия (точка 2), его потенциальная энергия равна нулю, а кинетическая максимальна 
. Максимальную скорость груза найдём из закона сохранения энергии (1.1.8):
За счёт запаса кинетической энергии груз совершает работу против упругой силы – 
и пролетает положение равновесия. Кинетическая энергия постепенно переходит в потенциальную. При 
груз имеет максимальное отрицательное смещение – А, кинетическая энергия Wk =0, груз останавливается и начинает движение к положению равновесия под действием упругой силы F= -kx. Далее движение происходит аналогично.
Маятники
Под маятником понимают твёрдое тело, которое совершает под действием силы тяжести колебания вокруг неподвижной точки или оси. Различают физический и математический маятники.
Математический маятник – это идеализированная система, состоящая из невесомой нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной материальной точке.
Математическим маятником, например, является шарик на длинной тонкой нити.
Отклонение маятника от положения равновесия характеризуется углом φ, который образует нить с вертикалью (рис.1.15). При отклонении маятника от положения равновесия возникает момент внешних сил (силы тяжести) 
: 
, где m – масса, 
– длина маятника
Этот момент стремится вернуть маятник в положение равновесия (аналогично квазиупругой силе) и направлен противоположно смещению φ, поэтому в формуле стоит знак «минус».
Уравнение динамики вращательного движения для маятника имеет вид: Iε= 
,
или
.
Будем рассматривать случай малых колебаний, поэтому sin φ ≈φ, обозначим 
,
имеем: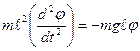 
, или 
, и окончательно
.
Это уравнение гармонических колебаний, его решение:
.
Частота колебаний математического маятника определяется только его длиной и ускорением силы тяжести, и не зависит от массы маятника. Период равен:
|
|
|
.
Если колеблющееся тело нельзя представить, как материальную точку, то маятник называют физическим (рис.1.1.6). Уравнение его движения запишем в виде:
.
В случае малых колебаний 
, или 
=0, где 
. Это уравнение движения тела, совершающего гармонические колебания. Частота колебаний физического маятника зависит от его массы, длины и момента инерции относительно оси, проходящей через точку подвеса.
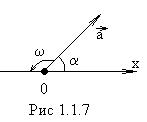
Обозначим 
. Величина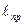 
называется приведённой длинной физического маятника. Это длина математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведённой длины от оси вращения, называется центром качания физического маятника (О’). Если маятник подвесить в центре качания, то приведённая длина и период колебаний будут теми же, что и в точке О. Таким образом, точка подвеса и центр качания обладают свойствами взаимности: при переносе точки подвеса в центр качения прежняя точка подвеса становится новым центром качения.
Математический маятник, который качается с таким же периодом, как и рассматриваемый физический, называется изохронным данному физическому маятнику.
1.1.4. Сложение колебаний (биения, фигуры Лиссажу). Векторное описание сложения колебаний
Сложение одинаково направленных колебаний можно производить методом векторных диаграмм. Любое гармоническое колебание можно представить в виде вектора следующим образом. Выберем ось х с началом отсчета в точке О (рис.1.1.7)
Из точки О построим вектор 
, который составляет угол 
с осью х. Пусть этот вектор поворачивается с угловой скоростью 
. Проекция вектора на ось Х равна:
то есть она совершает гармонические колебания с амплитудой а.
Рассмотрим два гармонических колебания одинакового направления и одинаковой циклической малой , заданные векторами 
и 
. Смещения по оси Х равны:
результирующий вектор имеет проекцию 
и представляет собой результирующее колебание (рис.1.1.8), по теореме косинусов 
Таким образом, сложение гармонических колебаний производится сложением векторов.
|
|
|
Проведем сложение взаимно перпендикулярных колебаний. Пусть материальная точка совершает два взаимно перпендикулярных колебания частотой :
.
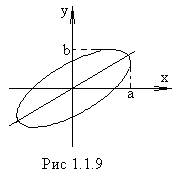
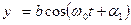Сама материальная точка при этом будет двигаться по некоторой криволинейной траектории.
Из уравнения движения следует: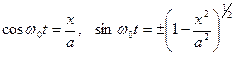 
,
тогда
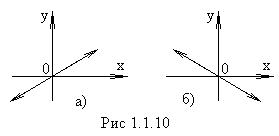
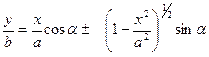. (1.1.9)
Из уравнения (1.1.9) можно получить уравнение эллипса (рис.1.1.9):
Рассмотрим частные случаи этого уравнения:
1. Разность фаз колебаний α= 0. При этом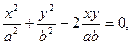 
т.е. 
или 
Это уравнение прямой, и результирующее колебание происходит вдоль этой прямой с амплитудой 
(рис.1.1.10).
2. Если разность фаз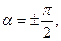 
то уравнение (1.1.9) переходит в уравнение эллипса, приведенного к координатным осям, 
При 
материальная точка движется по окружности, уравнение которой 
(рис.1.1.11).
3. Если частоты колебаний неодинаковы, то материальная точка описывает фигуры Лиссажу (рис.1112).
Рассмотрим сложение колебаний одного направления, частоты которых мало отличаются друг от друга. В этом случае результирующее движение можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такие колебания называются биениями.
Пусть частота одного колебания 
, второго 
. Амплитуды обоих колебаний одинаковы и равны а. Начальные фазы равны нулю. В таком случае уравнения колебаний имеют вид:
Сложим эти выражения:
(1.1.10)
График функции х(t) представлен на рис. 1.1.13. Множитель 
меняется гораздо медленнее, чем 
, поэтому (1.1.10) можно рассматривать как гармоническое колебание частоты , амплитуда которого меняется по некоторому периодическому закону
Частота изменения амплитуды – частота биений – равна разности частот складываемых колебаний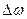 
.
Энергия колебаний
Смещение колеблющейся точки от положения равновесия, описывается уравнением:
ее ускорение равно второй производной от смещения по времени 
тогда сила, действующая на колеблющуюся точку, по второму закону Ньютона равна
- то есть сила пропорциональна смещению х и направлена против смещения к положению равновесия. Эта сила называется возвращающей силой. В случае груза на пружине возвращающей силой является сила упругости, в случае математического маятника – составляющая силы тяжести.
|
|
|
Возвращающая сила по характеру подчиняется закону Гука F= -kx, где 
– коэффициент возвращающей силы. Тогда потенциальная энергия колеблющейся точки равна:
(постоянную интегрирования выбирают равной нулю, чтобы при х =0 энергия Wn =0).
Кинетическая энергияосциллятора:
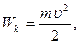
где 
, тогда 
Полная механическая энергия равна сумме кинетической и потенциальной энергий, 
и в случае свободных колебаний без трения сохраняется (рис.1.1.15). Когда материальная точка совершает колебания, кинетическая энергия переходит в потенциальную, и наоборот. В крайних точках (х = ±А) скорость 
, кинетическая энергия равна нулю, и полная энергия равна потенциальной:
Таким образом, полная механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия (х =0) потенциальная энергия переходит в кинетическую:
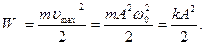
В промежуточных точках полная энергия равна
а скорость 
На рисунке 1.1.16 приведена кривая потенциальной энергии 
, горизонтальная линия соответствует полной энергии. Расстояние от этой линии до кривой равно кинетической энергии. Движение ограничено значениями х, заключёнными в пределах от –А до + А.
Средние за период значения кинетической и потенциальной энергии одинаковы и равны 
, так что средняя полная энергия системы равна полной энергии системы (средние значения 
).
Лекция 2
|
|
|
