 |
Моды поперечных колебаний непрерывной струны
|
|
|
|
Рассмотрим случай, когда N велико, тогда для двух первых мод между двумя соседними узлами окажется очень много грузов. Смещение будет медленно меняться от одного груза к другому, тогда можно считать, что все частицы в окрестности точки (x,y,z), соответствующей положению равновесия имеют один и тот же мгновенный вектор смещения  . Координаты x,y,z представляют собой равновесное состояние частиц и не зависят от времени.
. Координаты x,y,z представляют собой равновесное состояние частиц и не зависят от времени.
Пусть в состоянии равновесия струна растянута вдоль оси Х. Тогда координата х даёт положение равновесия каждого груза:
 ,
,
смещение вдоль оси Х -продольное, а вдоль осей Z и Y - поперечное. Для поперечных колебаний струны  , поэтому:
, поэтому:
 .
.
Для простоты положим, что колебания происходят только вдоль оси Z (Ψy =0). В этом случае говорят, что колебания линейно поляризованы вдоль оси Z.
Попытаемся найти нормальные моды непрерывной струны, которые представляют собой стоячие волны. Предположим, что мы возбудили какую-то моду, и все части струны совершают гармоническое движение с одинаковой частотой ω и одинаковой фазовой постоянной φ. Тогда функция  , представляющая собой смещение частиц, которые в равновесии находятся в х, должна иметь одну и ту же временную зависимость вида cos(ωt+φ) для всех движущихся элементов, то есть для всех х. Как обычно, фазовая постоянная соответствует моменту включения моды. «Геометрия» моды зависит от числа степеней свободы a, b, c …и т.д. и определяется отношением амплитуд колебаний А, В, С …и т.д., соответствующим этим степеням.
, представляющая собой смещение частиц, которые в равновесии находятся в х, должна иметь одну и ту же временную зависимость вида cos(ωt+φ) для всех движущихся элементов, то есть для всех х. Как обычно, фазовая постоянная соответствует моменту включения моды. «Геометрия» моды зависит от числа степеней свободы a, b, c …и т.д. и определяется отношением амплитуд колебаний А, В, С …и т.д., соответствующим этим степеням.
В случае непрерывной струны амплитуда колебаний для различных степеней свободы (то есть геометрия моды) может быть представлена в виде непрерывной функции от х – А (х). Функция А (х) характеризует моду; каждой моде соответствует своя А (х), тогда общее выражение для стоячей волны имеет вид:
|
|
|
 = А (х) cos(ωt+φ). (2.15)
= А (х) cos(ωt+φ). (2.15)
Для ускорения получаем:
 (2.16)
(2.16)
Вторая производная (2.15) по х равна
 (2.17)
(2.17)
Здесь знак частной производной ∂ заменен знаком полной производной d, так как А не зависит от времени.
Подставим (2.16) и (2.17) в общее уравнение волны и заменим y на  :
:
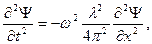
тогда имеем: 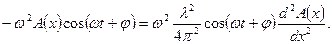 Сократив на cos(ωt+φ) и на
Сократив на cos(ωt+φ) и на  , получаем
, получаем 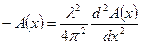 , или
, или
 .
.
Это уравнение определяет геометрическую форму моды. Здесь  – волновое число, поэтому
– волновое число, поэтому  тогда
тогда
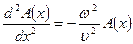 (2.18)
(2.18)
-каждой моде (то есть частоте ω) соответствует своя форма.
Уравнение (2.18) совпадает с уравнением гармонического осциллятора, в котором время заменено координатой. Решение этого уравнения имеет вид:

Тогда
 (2.19)
(2.19)
Дополним выражение (2.19) граничными условиями. Струна закреплена на концах, то есть при x= 0 и x=L  :
:
 отсюда В =0 и
отсюда В =0 и 
 , тогда
, тогда  , и
, и  Получаем условие образования стоячих волн в струне – по длине струны укладывается целое число полуволн. Из него имеем:
Получаем условие образования стоячих волн в струне – по длине струны укладывается целое число полуволн. Из него имеем:
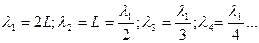
-это длины волн всех возможных мод, возникающих в струне.
Для частот имеем: 
Частоты  и т.д. называются второй, третьей и т.д. гармониками основной частоты
и т.д. называются второй, третьей и т.д. гармониками основной частоты  , соответствующих первой моде колебаний.
, соответствующих первой моде колебаний.
Важно помнить, что для всех гармоник (для всех мод) выполняется соотношение  , где
, где 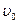 – фазовая скорость волны. Заменив
– фазовая скорость волны. Заменив  , получаем
, получаем  – это уравнение определяет ω как функцию волнового числа
– это уравнение определяет ω как функцию волнового числа  и называется дисперсионным соотношением или законом дисперсии. При этом
и называется дисперсионным соотношением или законом дисперсии. При этом 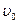 в общем случае не остается постоянной.
в общем случае не остается постоянной.
 Волны, удовлетворяющие простому дисперсному соотношению ω/k=const, называют недиспергирующими волнами.
Волны, удовлетворяющие простому дисперсному соотношению ω/k=const, называют недиспергирующими волнами.
Если отношение ω/k зависит от длины волны, а значит и от частоты, то волны называют диспергирующими. График зависимости ω от  в случае упругой струны представляет собой прямую линию, выходящую из начала координат.
в случае упругой струны представляет собой прямую линию, выходящую из начала координат.
Эффект Доплера
Рассмотрим волну, распространяющуюся в упругой среде. На некотором расстоянии от источника волны располагается устройство, воспринимающее колебания (приемник). Если источник и приемник неподвижны относительно среды, в которой распространяется волна, то частота колебаний, воспринимаемых источником, будет равна частоте  колебаний источника. Если же источник или приемник (либо оба) движутся относительно среды, то частота
колебаний источника. Если же источник или приемник (либо оба) движутся относительно среды, то частота  , воспринимаемая приемником, отличается от
, воспринимаемая приемником, отличается от  . Это явление называется эффектом Доплера.
. Это явление называется эффектом Доплера.
|
|
|
 Будем считать, что приемник и источник движутся вдоль соединяющей их прямой. Скорость источника
Будем считать, что приемник и источник движутся вдоль соединяющей их прямой. Скорость источника 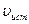 будем считать положительной, если источник движется по направлению к приемнику, и отрицательной, если источник удаляется от приемника. Аналогично скорость приемника
будем считать положительной, если источник движется по направлению к приемнику, и отрицательной, если источник удаляется от приемника. Аналогично скорость приемника 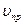 будем считать положительной, если приемник приближается к источнику, и отрицательной, если удаляется от него.
будем считать положительной, если приемник приближается к источнику, и отрицательной, если удаляется от него.
Если источник неподвижен и колеблется с частотой  , то к моменту, когда источник будет завершать
, то к моменту, когда источник будет завершать  -е колебание, порожденный первым колебанием гребень волны успеет пройти в среде путь
-е колебание, порожденный первым колебанием гребень волны успеет пройти в среде путь  (
( - скорость распространения волны относительно среды). Следовательно, порожденные волной за секунду
- скорость распространения волны относительно среды). Следовательно, порожденные волной за секунду  гребней и впадин волны уложатся по длине
гребней и впадин волны уложатся по длине  . Если же источник движется относительно среды со скоростью
. Если же источник движется относительно среды со скоростью 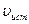 , то в момент, когда источник будет завершать
, то в момент, когда источник будет завершать  -е колебание, гребень, порожденный первым колебанием, будет находиться от источника на расстоянии
-е колебание, гребень, порожденный первым колебанием, будет находиться от источника на расстоянии 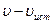 (рис. 2.7). Следовательно,
(рис. 2.7). Следовательно,  гребней и впадин волны уложатся на длине
гребней и впадин волны уложатся на длине 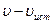 , так что длина волны будет равна
, так что длина волны будет равна
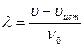 .
.
Мимо неподвижного источника пройдут за секунду гребни и впадины, укладывающиеся по длине  . Если приемник движется со скоростью
. Если приемник движется со скоростью 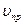 , то в конце секундного промежутка времени он будет воспринимать впадину, которая в начале этого промежутка отстояла от его теперешнего положения на
, то в конце секундного промежутка времени он будет воспринимать впадину, которая в начале этого промежутка отстояла от его теперешнего положения на  . Таким образом, приемник воспринимает за секунду колебания, отвечающие гребням и впадинам, укладывающимся на длине
. Таким образом, приемник воспринимает за секунду колебания, отвечающие гребням и впадинам, укладывающимся на длине  (рис.2.8) и будет колебаться с частотой
(рис.2.8) и будет колебаться с частотой

 .
.
Подставив  из полученного ранее выражения, получаем
из полученного ранее выражения, получаем
 .
.
Если расстояние между источником и приемником сокращается, воспринимаемая приемником частота оказывается больше частоты источника  . Если расстояние между источником и приемником растет, воспринимаемая частота будет меньше
. Если расстояние между источником и приемником растет, воспринимаемая частота будет меньше  .
.
|
|
|
Лекция 8
2 .10. Электромагнитные волны
2.10.1. Волновые уравнения для электромагнитного поля. Плоские и сферические электромагнитные волны. Волновой вектор. Волновое уравнение для электромагнитного поля. Основные свойства электромагнитных волн
Итак, переменное электрическое поле порождает переменное магнитное поле. Это переменное магнитное поле порождает электрическое и т.д. Таким образом, если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то в окружающем заряды пространстве возникает последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке. Этот процесс является периодическим в пространстве и во времени и представляет собой волну. Найдём уравнение этой волны.
В случае однородной нейтральной непроводящей среды с постоянными проницаемостями ε и μ имеем:

Поэтому уравнения Максвелла можно записать в виде:
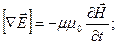 (2.20)
(2.20)
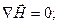 (2.21)
(2.21)
 (2.22)
(2.22)
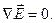 (2.23)
(2.23)
Возьмём ротор от обеих частей уравнения (2.20):

Изменим порядок дифференцирования по координатам ( ) и времени (dt), получим:
) и времени (dt), получим:

Подставив выражение (2.22), получим  Известно, что
Известно, что  Однако
Однако  , поэтому
, поэтому  Тогда:
Тогда:  или
или
 (2.24)
(2.24)
Взяв ротор от обеих частей уравнения (2.22) и произведя аналогичные преобразования, получим:
 (2.25)
(2.25)
(2.24)и (2.25)– это типичные волновые уравнения. Они описывают электромагнитную волну, фазовая скорость которой  В вакууме μ =1, ε =1, и
В вакууме μ =1, ε =1, и 
Рассмотрим плоскую электромагнитную волну, распространяющуюся в нейтральной непроводящей среде с постоянными проницаемостями ε и μ (ρ =0,  , ε =const, μ =const). Направим ось Х перпендикулярно к волновым поверхностям. Тогда
, ε =const, μ =const). Направим ось Х перпендикулярно к волновым поверхностям. Тогда  и
и  не будут зависеть от координаты х, а будут зависеть только от координат y и z. Поэтому уравнения Максвелла (2.20) - (2.25) можно упростить и представить в виде:
не будут зависеть от координаты х, а будут зависеть только от координат y и z. Поэтому уравнения Максвелла (2.20) - (2.25) можно упростить и представить в виде:

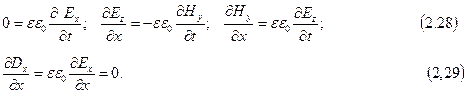
Уравнения (2.29) и (2.28) показывают, что Еx не зависит ни от х, ни от t. Уравнения (2.27) и (2.26) дают такой же результат для Нх. Следовательно, отличные от нуля Ех и Нх могут быть обусловлены лишь постоянными однородными полями, накладывающимися на электромагнитное поле волны. Само поле волны не имеет составляющих вдоль оси Х. Отсюда следует, что векторы  и
и  перпендикулярны к направлению распространения волны, то есть электромагнитные волны поперечны.
перпендикулярны к направлению распространения волны, то есть электромагнитные волны поперечны.
|
|
|
Два последних уравнения (2.26) и (2.28) можно объединить в две независимые группы:

Первая группа уравнений связывает компоненты Ey и Hz, вторая – компоненты E zи Hy. Допустим, что первоначально было создано переменное электрическое поле Еу, направленное вдоль оси У. Согласно второму из уравнений (2.30) это поле создаёт магнитное поле Нz, направленное вдоль оси Z. В соответствии с первым уравнением (2.30) поле Нz создаёт электрическое поле Еу, и т.д. Ни поле Еz, ни поле Ну при этом не возникают. Аналогично, если первоначально было создано поле Еz, то согласно уравнениям (2.31) появится поле Ну, которое возбудит поле Еz, и т.д. В этом случае не возникают поля Еу и Нz. Таким образом, для описания плоской электромагнитной волны достаточно взять одну из систем уравнений (2.30) или (2.31), положив компоненты, фигурирующие в другой системе, равными нулю.
Возьмём для описания волны уравнение (2.30), положив  ,
, 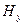 =0. Продифференцируем первое уравнение по х и произведём замену:
=0. Продифференцируем первое уравнение по х и произведём замену:

Подставим ∂ Hz/∂x из второго уравнения, получим волновые уравнения для Еу:
 (2.32)
(2.32)
Здесь заменили 
Продифференцируем по х второе уравнение из (2.30), найдём после аналогичных преобразований волновое уравнение для Hz:
 (2.33)
(2.33)
Полученные уравнения представляют собой частные случаи уравнений (2.23) и (2.24). Так как Ex=Ez =0 и Hx=Hy =0, то Ey=E; Hz=H. Индексы у и z при E и H мы сохранили, чтобы подчеркнуть, что  и
и  перпендикулярны.
перпендикулярны.
Простейшим решением уравнений (2.32) и (2.33) является:
 , (2.34)
, (2.34)
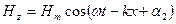 , (2.35)
, (2.35)
где ω – частота волн,  – волновое число,
– волновое число,  – начальные фазы колебаний в точке х =0.
– начальные фазы колебаний в точке х =0.
Подставим (2.34) и (2.35) в (2.30):

 .
.
Для удовлетворения этих уравнений необходимо, чтобы  , кроме того, должны выполняться соотношения:
, кроме того, должны выполняться соотношения:

Перемножим два последних равенства: 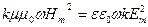 , или
, или  .
.
Таким образом, колебания электрического и магнитного векторов в электромагнитной волне происходят в одной фазе  , а амплитуды этих векторов связаны соотношением:
, а амплитуды этих векторов связаны соотношением:
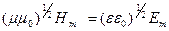
Для волны, распространяющейся в вакууме  Ом.
Ом.
В векторной форме (2.34) и (2.35) примут вид  :
:

Векторы  и
и  образуют с направлением распространения волны правовинтовую систему.
образуют с направлением распространения волны правовинтовую систему.
|
|
|


