 |
Волновое уравнение в пространстве. Плоская гармоническая волна. Длина волны, волновое число, фазовая скорость. Одномерное волновое уравнение. Упругие волны в газах, жидкостях и твердых телах
|
|
|
|
Уравнением волны называется зависимость от координат и времени параметров среды при прохождение в ней волны 
. Эта функция должна быть периодической как относительно времени, так и относительно координат.
Найдем функцию в случае плоской поперечной волны, полагая, что колебания носят гармонический характер, а волна распространяется в направлении оси Х (рис.2.2).
Рассмотрим точку М, которая является источником колебаний. Ее колебания относительно положения равновесия (точки О) описываются уравнением 
время t будем отсчитывать от начала колебаний точки М. Через время t колебания достигаютточки В, которая начинает колебаться относительно своего положения равновесия точки О 1.Волновой процесс распространяется при этом на расстояние ОО 1= x. Найдем уравнение колебаний точки В относительно ее положения равновесия О 1. Обозначим время от начала колебаний в О 1 до рассматриваемого момента через t 1, тогда отклонение точки В через время t 1 после начала колебаний равно 
, однако t=t + t 1, т.е. t 1= t - t, тогда
(2.1)
За время Т колебание распространилось на l, а за t - на расстояние 
,т.е.
(2.2)
Подставим (2.2) в (2.1):
(2.3)
Величина 
называется волновым числом, 
тогда 
- это уравнение волны, определяющее смещение любой точки В волнового фронта для любого момента времени t, отсчитываемого от момента возникновения колебания в начале О, по отношению к которому дана координата х точки В. Уравнение волны, распространяющейся в сторону убывания х, отличается только знаком: 
.
Здесь 
- фаза точки В в момент t. В этот же момент времени фаза точки М равна wt = 2 pt/T, тогда 
называют разностью фаз колебаний в точках М и В. Тогда уравнение волны (2.3) примет вид: 
. Таким образом,
|
|
|
(2.4)
- путь волны в долях длины волны, запаздывание в долях периода и разность фаз в долях окружности выражаются одним и тем же числом. Уравнение колебаний точки В имеет вид:
(2.5)
Дважды дифференцируем уравнение волны (2.3) по х, имеем
(2.6)
Подставим (2.6) в (2.5): 
учитывая, что 
получаем
(2.7)
Это общее уравнение волны, распространяющейся в направлении Х. Оно связывает величины 
, х, t для любой точки при прохождении волны через эту точку.
Для волны, распространяющейся в произвольном направлении 
, уравнение волны имеет вид
где 
- лаплассиан . Решение этого уравнения 
.
При выводе уравнения (2.3) мы предполагали, что амплитуда колебаний не зависит от х. Для плоской волны это наблюдается в тех случаях, когда энергия волны не поглощается средой. При распространении в поглощающей энергию среде интенсивность волны по мере удаления от источника уменьшается, следовательно, уменьшается и амплитуда - волна затухает. В однородной среде такая волна описывается уравнением 
, где 
- амплитуда в точках плоскости r =0.
Теперь найдем уравнение сферической волны. Всякий реальный источник волн обладает некоторой протяженностью. Однако на расстояниях r много больших размеров источника, последний можно считать точечным. В изотропной и однородной среде волна, распространяющаяся от точечного источника, будет сферической. Пусть фаза колебаний источника равна 
. Тогда точки, лежащие на волновой поверхности радиуса r, будут колебаться с фазой 
Амплитуда колебаний в этом случае, даже если энергия волны не поглощается средой, не остается постоянной – она убывает с расстоянием от источника по закону 
, поэтому уравнение сферической волны имеет вид
где а - амплитуда колебаний на расстоянии 1м от источника. Дли поглощающей среды 
Итак, скорость распространения волны есть скорость распространения колебательного процесса, не совпадающая со скоростью колебаний отдельных частиц среды, которые осуществляют этот процесс. Величина скорости зависит и от того, в каком направлении ее измерять.
|
|
|
Скорость перемещения в пространстве точек волновой поверхности, колеблющихся в одной фазе, называется фазовой скоростью волны 
(в рассматриваемых ранее уравнениях – фазовая скорость) Фазовая скорость поперечных волн в изотропной однородной среде 
, где s - модуль сдвига, r - плотность среды. Распространение продольных волн в тонком длинном стержне связанно с его продольным растяжением и сжатием, фазовая скорость таких волн 
, где Е – модуль Юнга для стержня.
Энергия волны
Рассмотрим плоскую продольную волну, распространяющуюся в направление оси Х. Пусть волна является бегущей, т.е. ее распространение связанно с распространением в пространстве энергии колебаний. Уравнение волны
(2.8)
Выделим в среде элементарный объем 
настолько малый, что скорости движения и деформации во всех его точках одинаковы.
Выделенный объем обладает кинетической энергией
где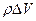 
- масса объема, 
- скорость. Разделив эту энергию на величину объема, получим объемную плотность кинетической энергии
(2.9)
Рассматриваемый элемент объема обладает потенциальной энергией упругой деформации. Чтобы найти эту энергию, представим выделенный объем в виде стержня с площадью поперечного сечения S и длиной 
. Один конец стержня закреплен, ко второму приложим растягивающую силу 
и будем медленно увеличивать ее от 0 до 
. Удлинение стержня будет при этом меняться от 0 до х. По закону Гука 
где 
- коэффициент упругости. Работа силы упругости в этом процессе
Эта работа идет на увеличение упругой энергии U. т.е. 
Плотность этой энергии
(2.10)
где 
- напряжение, Е – модуль Юнга, 
- относительная деформация. Так как фазовая скорость волны , то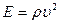 
, и объемная плотность потенциальной энергии равна 
Под объемной плотностью энергии упругих волн понимают объемную плотность 
механической энергии среды, обусловленную распространением этих волн:
. (2.11)
Продифференцируем уравнение (2.8) сначала по времени, а затем по координате х
Подставив производные по координате и по времени в (2.11) и заменив 
, имеем
- в каждой точке среды, охваченной волновым движением, объемные плотности кинетической и потенциальной энергий являются одинаковыми функциями времени. Объемная плотность энергии волны изменяется с течением времени, это связанно с процессами распространения волн, так как волновой процесс сопровождается переносом энергии при вовлечении в колебательное движение все новых частиц. Поэтому объемная плотность энергии волн зависит как от координат, так и от времени.
|
|
|
Среднее за период значение объемной плотности энергии 
. Плотность энергии волны и ее среднее значение пропорциональны плотности среды 
, квадрату частоты 
и квадрату амплитуды 
.
Таким образом, среда, в которой распространяется волна, обладает дополнительной энергией, которая доставляется от источника колебаний в различные точки среды самой волной, т.е. волна переносит с собой энергию. Скорость переноса энергии волной равна скорости перемещения в пространстве поверхности, соответствующей максимальному значению объемной плотности энергии волны. Для синусоидальных волн эта скорость равна фазовой скорости (рис 2.3).
Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии через эту поверхность. Если через данную поверхность за время dt переносится энергия dW, то поток энергии Ф равен
Поток энергии в разных точках различен. Для характеристики значения энергии в разных точках пространства вводится вектор плотности потока энергии (вектор Умова). Он численно равен потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению переноса энергии и направлен в сторону переноса энергии:
где 
- единичный вектор, совпадающий по направлению с распространением волны.
Очевидно, за время 
через площадку 
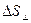будет перенесена энергия 
, заключенная в объеме цилиндра с основанием 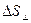и высотой 
, где - фазовая скорость волны, 
Тогда плотность потока энергии
здесь 
- вектор, численно равный фазовой скорости и направленный в сторону переноса энергии волной.
Интенсивностью волны I называется модуль среднего значения вектора Умова. Интенсивность волны численно равна энергии, переносимой волной за единицу времени сквозь единицу площади поверхности, нормальной к направлению распространения волны. Для синусоидальной волны
|
|
|
Поток энергии через некоторую поверхность S равен потоку вектора 
через эту поверхность
Среднее значение потока энергии через произвольную волновую поверхность незатухающей сферической волны (в каждой точке поверхности векторы и 
совпадают):
где r – радиус волновой поверхности. Энергия волны не поглощается средой, поэтому средний поток энергии через сферу любого радиуса должен иметь одинаковое значение, т.е. выполняется соотношение
- амплитуда 
незатухающей сферической волны обратно пропорциональна расстоянию r от источника волны. Тогда средняя плотность потока энергии обратно пропорциональна квадрату расстояния от источника.
В случае плоской затухающей волны амплитуда убывает с расстоянием по закону 
, и средняя плотность потока энергии (т.е. интенсивность) убывает по закону 
, где 
- коэффициент поглощения волны.
Принцип суперпозиции волн
Принцип суперпозиции волн состоит в следующем. В линейной среде волны распространяются независимо друг от друга, так что результирующее возмущение в какой–либо точке среды при распространении в ней нескольких волн равно сумме возмущений, соответствующих каждой из этих волн порознь. Для смещений имеем 
; 
для скорости частиц среды 
; и для ускорения 
.
Несинусоидальную волну можно заменить эквивалентной ей суммой синусоидальных волн, т.е. представить ее в виде группы волн или волнового пакета. Совокупность значений частот этих синусоидальных волн называется спектром частот волны.
Простейшей группой волн является квазисинусоидальная плоская волна, которая получается в результате наложения двух распространяющихся вдоль оси ОХ плоских волн с одинаковыми амплитудами и близкими по значению частотами и волновыми числами 
Эта волна отличается от синусоидальной тем, что ее амплитуда является функцией времени и координат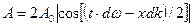 
.
За скорость распространения этой несинусоидальной волны принимают скорость и перемещения точки М, в которой амплитуда А имеет какое- то фиксированное значение (А =0, А =2 А 0 и т.п.). Точка М движется по закону
т.е. 
. Cкорость и называется групповой скоростью волны.
Лекция 7
Образование стоячих волн
Когда в некоторой точке тела (в струне, в трубе) возникает колебательное движение, оно волнообразно распространяется до границ тела. Там энергия волны разделяется – часть её проникает в среду, окружающую тело (например, в воздух), часть остаётся в теле и обуславливает появление отражённой волны. Эта волна, распространяясь в теле, встречается с новыми волнами, движущимися к границе тела. В результате сложения колебаний двух волн образуется стоячая волна (рис.2.4).
|
|
|
Уравнения двух плоских волн, распространяющихся в противоположных направлениях:
Сложим оба уравнения, имеем 
Известно, что k =2 π/λ, тогда
(2.12)
Это и есть уравнение стоячей волны. Оно показывает, что все точки стоячей волны колеблются с одинаковой частотой, амплитуда зависит от х:
(2.13)
В точках, где 
амплитуда колебаний максимальна и равна: А =2 а.
Эти точки – пучности стоячей волны, их координаты:
. (2.14)
В точках, где 
амплитуда колебаний обращается в ноль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах колебаний не совершают, их координаты:
Таким образом, расстояние между двумя пучностями равно расстоянию между двумя узлами, и равно λ /2. Пучности и узлы сдвинуты друг относительно друга на λ /4.
Из выражения (2.13) видно, что амплитуда при переходе через нулевое значение меняет знак. Таким образом, фаза колебаний по разные стороны от узла отличается на π, то есть точки, лежащие по разные стороны узла, колеблются в противофазе. Все точки, заключённые между двумя узлами, колеблются в фазе.
|
|
|
