 |
Закон сохранения энергии для изолированной системы «поле- заряды»
|
|
|
|
Рассмотрим изолированную систему поле -заряды. Изолированность системы следует понимать как отсутствие потока энергии через ограничивающую ее поверхность и отсутствие потока массы, который тоже уносил бы энергию. В таком случае убыль энергии электромагнитного поля в единицу времени равна
- работе, совершаемой полем над зарядами.
Ясно, что работа, производимая над зарядами, является мерой превращения энергии поля в другие виды: в кинетическую энергию заряженных частиц и тел, потенциальную энергию деформации, внутреннюю энергию среды и т.д. Для дискретной системы зарядов
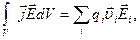
тогда подставляя в (2.42) выражение (2.36), получаем
.
Из этого выражения следует, что
В последнем равенстве объем V может быть или конечным, или охватывать все пространство. Это соотношение выражает закон сохранения энергии в изолированной системе поле-заряды: в изолированной системе поле-заряды сохраняется сумма энергии поля и релятивистской энергии заряженных материальных точек.
Импульс электромагнитного поля. Закон сохранения импульса и момента импульса
Просуммируем все уравнения движения частиц, находящихся в поле, в выражении (2.36)
.
Будем считать распределение зарядов в пространстве непрерывным, поэтому сумму заменим интегралом по объему системы:
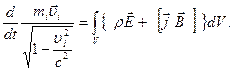(2.45)
Подставим значения 
и 
из уравнений Максвелла:
. (2.46)
Чтобы в правой части этого равенства получить производную по времени, дополним его слагаемым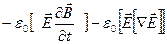 
. Это равенство всегда равно нулю, так как 
, т.е. 
, тогда
Таким образом, равенство (2.46) не нарушается. Кроме того, добавим еще 
. Очевидно, 
, так как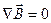 
. Получаем:
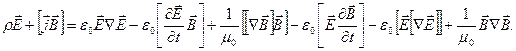
Сгруппируем:
Подставив в выражение (2.45), получаем
В случае изолированной системы поле-заряды второй и третий интегралы можно свести к поверхностным, и при интегрировании по всему пространству они дают 0. В результате имеем
|
|
|
,
или
(2.47)
- это закон сохранения импульса для изолированной системы поле-заряды.
Величина
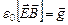(2.48)
есть плотность импульса.
Выражение (2.47) можно сформулировать так: в изолированной системе поле-заряды полный импульс, равный релятивистскому импульсу заряженных частиц и импульсу электромагнитного поля, сохраняется.
Из выражения (2.48) следует, что плотность импульса 
отлична от нуля только в том случае, если существуют оба поля 
и 
, непараллельные друг другу.
Взаимодействие между заряженными телами осуществляется посредством поля. Это приводит к несохранению импульса замкнутой механической системы материальных точек, если система обменивается импульсом с полем так, что импульс поля изменяется. В такой системе может не выполняться третий закон Ньютона. Например, излучающее, рассеивающее, отражающее или поглощающее электромагнитные волны тело испытывает со стороны поля действие силы, т.к. импульс тела меняется, но эта сила не имеет противодействующей – к полю не может быть приложена сила.
Обладая импульсом, электромагнитное поле оказывает давление на тела, с которыми взаимодействует. Примером тому – световое давление.
Плотность момента импульса электромагнитного поля найдем по правилу, известному из механики:
где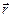 
- радиус-вектор точки, в которой определяются и 
. Умножая (2.47) векторно справа на 
, получаем закон сохранения момента импульса в изолированной системе поле-заряды:
.
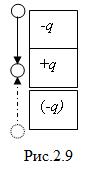
Из (2.47) следует, что 
.
Излучение диполя
Простейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь. Примером такого диполя служит система, образованная неподвижным точечным зарядом + q и колеблющимся около него точечным зарядом – q (рис.2.9).
|
|
|
Дипольный электрический момент этой системы изменяется со временем по закону:
,
где 
-радиус-вектор заряда – q, 
-амплитуда колебаний, 
-единичный вектор, направленный вдоль оси диполя, 
.
Пусть размеры диполя малы в сравнении с длиной волны, << λ. Такой диполь называют элементарным. Если волна распространяется в однородной изотропной среде, то в волновой зоне, то есть при r>>λ, волновой фронт будет сферическим. Векторы 
и 
в каждой точке перпендикулярны к лучу, то есть к радиус-вектору, проведённому в данную точку из центра диполя (рис.2.10).
Назовём сечения волнового фронта плоскостями, проходящими через ось диполя, меридианами, а плоскостями, перпендикулярными к оси диполя, - параллелями. Тогда вектор в каждой точке волновой зоны направлен по касательной к меридиану, а вектор – по касательной к параллели. Если смотреть вдоль луча , то картина будет такая же, как на рис. 2.11.
Амплитуды 
и 
зависят от расстояния r до излучателя и от угла 
между направлением радиус-вектора и осью диполя (рис.2.11):
Тогда средняя плотность потока энергии 
и если = const, то интенсивность волны изменяется вдоль луча пропорционально квадрату расстояния от излучателя. При = π /2 плотность потока энергии максимальна. В направлениях, совпадающих с осью, =0, = π, диполь не излучает. Зависимость интенсивности от угла очень наглядно представляется диаграммой направленности диполя (рис.2.12). Она строится так, чтобы длина отрезка, отсекаемого им на луче, проведённом из центра диполя, давала интенсивность излучения под углом .
Мощность излучения 
, где р – дипольный момент. Подставив выражение для дипольного момента, получаем 
тогда средняя мощность 
где а – ускорение колеблющегося заряда.
Эта формула определяет мощность излучения не только при колебаниях, но и при произвольном движении заряда. Всякий заряд, движущийся с ускорением, возбуждает электромагнитные волны.
Заряд, совершающий гармонические колебания, излучает монохроматическую волну с частотой, равной частоте колебаний заряда. Если электрон движется с постоянной скоростью, а= 0, то излучения нет, если скорость заряда 
не превышает скорости света в этой среде св= c/(εμ) ½. Если > св, имеет место излучение Вавилова – Черенкова.
|
|
|
|
|
|
