 |
Работа, совершаемая полем при перемещении зарядов
|
|
|
|
Определения кинетической и потенциальной энергии, а также импульса и момента импульса, данные в механике для материальной точки и системы материальных точек, отнюдь не распространяются на поля.
Рассмотрим систему заряженных материальных точек, взаимодействующих между собой. Такая система описывается уравнениями Максвелла-Лоренца. Пользуясь этими уравнениями, распространим понятия энергии и импульса на поля, находя величины, сохраняющиеся для изолированной системы поле - заряды. Макроскопические электрические заряды, так или иначе, связаны с материальными телами, на которых они расположены. Пусть частица массой
несет заряд 
. Тогда по второму закону Ньютона уравнения движения имеют вид:
. (2.36)
Умножим это выражение на 
, получим выражение для энергии
В правой части этого выражения стоит работа силы Лоренца. Она совершается только электрической составляющей этой силы, так как магнитная составляющая равна нулю (векторы 
и коллинеарны).
Левую часть преобразуем с помощью тождества
.
Действительно, 
, тогда в левой части
в правой части
Тогда окончательно получаем
- элементарная работа силы Лоренца равна приросту релятивистской кинетической энергии заряженной материальной точки.
Просуммируем теперь элементарные работы по всем точкам системы и разделим на dt:
(2.37)
(здесь на dt разделили левую и правую части).
Формула (2.37) выражает теорему об изменении энергии системы материальных точек в единицу времени за счет работы поля, совершенной над ними. Выведенная формула для точечного заряда обобщается и на случай непрерывно распределенного в пространстве заряда. Для работы поля в единицу времени имеем:
|
|
|
причем 
- плотность тока, 
- заряд одного носителя, 
- число носителей в единице объема. Тогда
. (2.38)
Мощность, заключенная в единице объема (плотность мощности) равна
Итак, за счет работы поля изменяется кинетическая энергия находящихся в поле заряженных частиц. При этом энергия поля превращается в кинетическую энергию частиц.
2.10.2.3. Энергия электромагнитного поля. Плотность и поток энергии. Закон изменения энергии
Найдем энергию электромагнитного поля по заданным значениям векторов 
и 
. Для этого используем уравнения Максвелла
Умножим первое уравнение на 
, второе – на 
получаем
Из равенства (2.39) вычтем (2.40), имеем
(2.41)
Из математики известно, что 
Левая часть выражения (2.41) есть частная производная по времени от функции 
Тогда имеем: 
или
Проинтегрируем это выражение по объему V:
Преобразуем: 
Получаем
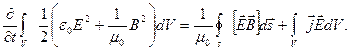(2.42)
Но 
- работа поля за единицу времени в пределах конечного объема V. Тогда 
- плотность энергии электромагнитного поля. Она равна сумме плотностей энергий электрического и магнитного полей. 
- плотность потока энергии, называемая вектором Пойтинга. Этот вектор направлен в сторону перемещения энергии и по абсолютному значению равен энергии, которая в единицу времени переносится полем через единичную площадку, ориентированную перпендикулярно потоку.
Тогда энергия поля в заданном объеме V равна
Поток энергии поля через замкнутую поверхность в единицу времени определяет полную мощность излучения системы зарядов и равен
Таким образом, равенство (2.42) – это математическое выражение закона изменения энергии электромагнитного поля. Его можно переписать в виде:
(2.43)
(W не зависит от координат точек поля и частную производную можно заменить полной). Теорема (2.43) читается так: убыль энергии в некотором объеме равна потоку энергии, выходящему из объема, и работе, совершаемой полем над зарядами в этом объеме. В дифференциальной форме эта теорема имеет вид:
|
|
|
В области, где нет зарядов и токов (
), плотность электромагнитной энергии связана с ее потоком 
уравнением непрерывности:
(2.44)
Это уравнение является локальным выражением закона сохранения энергии для электромагнитного поля при отсутствии зарядов. Оно выражает теорему Пойтинга.
Проинтегрируем (2.44) по объему V, ограничивающему поверхность s:
Таким образом, при отсутствии зарядов убыль энергии поля в объеме V в единицу времени равна интегральному потоку энергии через поверхность, ограничивающую этот объем.
Если потока энергии через границы поля нет, 
, и энергия поля убывает, если 
- заряды движутся под действием сил поля. Если же 
, то энергия поля растет, но в этом случае работают не силы поля, а сторонние силы, не сводящиеся к силе Лоренца.
|
|
|
