 |
Глава 2. Матрицы и определители.
|
|
|
|
Основные сведения о матрицах.
Определение. Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца. Матрицы обозначаются прописными (заглавными) буквами латинского алфавита: A,B,C, … Например, матрица
А = 
Или, в сокращенной записи, А = (aij); i = 1,2, …, m; j = 1,2,…,n. (Пример).
Наряду с круглыми скобками используются и другие обозначения матрицы: [ ], çç ÷÷.
Определение. Две матрицы А и В одинаковых размеров называются равными Аm´n=Bm´n, если все элементы с одинаковыми индексами обеих матриц совпадают, т.е. aij=bij для любых i = 1,2, …, m; j = 1,2,…,n.
Определение. Матрица размера 1´n, состоящая из одной строки, называется матрицей (вектором) – строкой, матрица размера m´1, состоящая из одного столбца – матрицей (вектором) – столбцом, а матрица размера 1´1 – скалярной матрицей.
Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной. (Пример).
Определение. Если матрица квадратная, то совокупность тех ее элементов aii. у которых номер строки равен номеру столбца, называется главной диагональю или просто диагональю матрицы. Таким образом, главную диагональ квадратной матрицы образуют элементы a11, a22,..., ann.
Определение. Квадратная матрица называется диагональной, если все ее недиагональные элементы равны нулю, т.е. это матрица вида 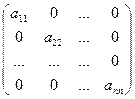 .
.
Определение. Если у диагональной матрицы n-ого порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-ого порядка; она обозначается буквой Е:
|
|
|
Е = 
Определение. Если amn = anm, то матрица называется симметрической.
Пример. 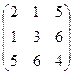 - симметрическая матрица
- симметрическая матрица
Определение. Если все элементы матрицы любых размеров равны нулю, то она называется нулевой или нуль-матрицей.
Операции над матрицами.
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что, они определены только для матриц одинакового размера. Таким образом, можно определить операции сложения и вычитания матриц:
Определение. Суммой (разностью) матриц A и B одинаковых размеров m´n является матрица С = А + В того же размера, элементы которой равны сумме соответствующих элементов исходных матриц, т.е.: cij = aij ± bij, i = 1,2, …, m; j = 1,2,…,n.
Определение. Произведением матрицы А на число a называется матрица В = aА, элементы которой bij = a aij, i = 1,2, …, m; j = 1,2,…,n.
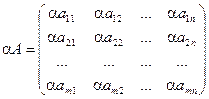
Пример. Даны матрицы А = 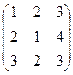 ; B =
; B = 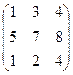 , найти 2А + В.
, найти 2А + В.
Определение: Произведением матриц Аm´k×Bk´n называется такая матрица Сm´n, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В: 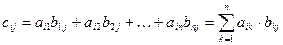 , i = 1,2, …, m; j = 1,2,…,n.
, i = 1,2, …, m; j = 1,2,…,n.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Пример. Вычислить произведение А×В, где
А= 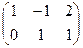 ; В =
; В = 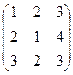 .
.
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (это следует из определения этих операций)
Свойства операции над матрицами.
1) А + В = В + А;
2) (А + В) + С = А + (В + С);
3) a(А + В) = aА + aВ;
4) А×(В + С) = А×В + А×С;
5) (А + В)×С = А×С + В×С;
I. a(А ×В) = (aА)В = А(aВ);
7) (АВ)С = А(ВС).
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
|
|
|
I. Если произведение матриц АВ существует, то после перестановки сомножителей произведение матриц ВА может и не существовать. Действительно, в примере, приведенном выше, получили произведение матриц А2´3×B3´3 = С2´3, а произведение В3´3×А2´3 не существует.
II. Если даже произведения АВ и ВА существует, то они могу быть матрицами разных размеров. Например, А2´3×B3´2= С2´2, а В3´2×А2´3= D3´3.
III. Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения и обе матрицы одинакового размера (это возможно только при умножении квадратных матриц А и В одинакового порядка).
Пример. Найти произведения АВ и ВА, где
А = 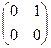 , В =
, В = 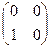 .
.
Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными (коммутирующими между собой).
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой квадратной матрицей того же порядка:
А×Е = Е×А = А
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
Очевидно, что для любых матриц выполняются следующее свойство:
A×O = O; O×A = O,
где О – нулевая матрица.
IV. Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что АВ = 0, не следует, что А=0 или В=0. Например, А= 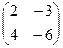 , B=
, B= 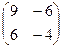 , но АВ =
, но АВ = 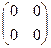 = 0.
= 0.
V. Важным частным случаем произведения матриц является произведение квадратной матрицы Аn´n на вектор-столбец Х = 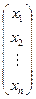 :
:
А× Х = 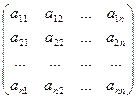 ×
× 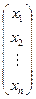 =
= 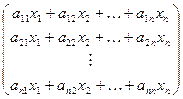 = x1
= x1 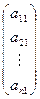 + x2
+ x2 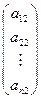 +... + xn
+... + xn 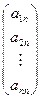 , т.е. вектор А× Х является линейной комбинацией столбцов матрицы А с коэффициентами xi.
, т.е. вектор А× Х является линейной комбинацией столбцов матрицы А с коэффициентами xi.
Аналогично при умножении матрицы А на вектор-строку(слева) Х А мы получаем вектор-строку, являющийся линейной комбинацией строк матрицы А с коэффициентами xi.
Рассмотрим еще одну операцию – транспонирование матрицы
Определение. Транспонирование матрицы – переход от матрицы А к матрице АТ, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица АТ называется транспонированной относительно матрицы А:
А =  ; АТ=
; АТ= 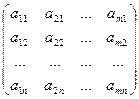 ;
;
Из определения следует, что если матрица А имеет размер m´n, то транспонированная матрица АТ имеет размер n´m.
|
|
|
Свойства операции транспонирования:
1) (АТ)Т = А;
2) (kA)T = kAT;
3) (A + B)T = AT + BT;
4) (АВ)Т = ВТАТ.
Пример. Даны матрицы А = 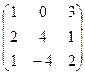 , В =
, В =  , С =
, С = 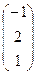 и число a = 2. Найти АТВ+aС.
и число a = 2. Найти АТВ+aС.
|
|
|


