Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется нормирующем множителем, то получим

 

xcosj + ysinj - p = 0 –

нормальное уравнение прямой.

 

Знак ± нормирующего множителя надо выбирать так, чтобы m×С < 0.

р – длина перпендикуляра, опущенного из начала координат на прямую, а j - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

 

Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.

уравнение этой прямой в отрезках:

уравнение этой прямой с угловым коэффициентом: (делим на 5)

нормальное уравнение прямой:

 

; cosj = 12/13; sinj = -5/13; p = 5.

Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.

 

Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см².

 

Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.

Уравнение прямой имеет вид: , где х₁ = у₁ = 0; x₂ = -2; y₂ = -3.

Угол между прямыми на плоскости.

Определение. Если заданы две прямые y = k₁x + b₁, y = k₂x + b₂, то острый угол между этими прямыми будет определяться как

.

 

Две прямые параллельны, если k₁ = k₂.

 

Две прямые перпендикулярны, если k₁ = -1/k₂.

 

Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = lА, В₁ = lВ. Если еще и С₁ = lС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Расстояние от точки до прямой.

Теорема. Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как

.

 

Доказательство. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:

(1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

.

Теорема доказана.

 

Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.

 

 

Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

 

.

 

Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

 

 

§3.Кривые второго порядка.

Уравнение вида

Ах² + Вху + Су² + Dx + Ey + F = 0,

где хотя бы одна из трех величин А, В или С не равна нулю, называется уравнение второго порядка, а линия, представляемая таким уравнением – линией второго порядка.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) 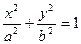- уравнение эллипса.

2) - уравнение “мнимого” эллипса.

3) 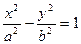- уравнение гиперболы.

4) a²x² – c²y² = 0 – уравнение двух пересекающихся прямых.

5) y² = 2px – уравнение параболы.

6) y² – a² = 0 – уравнение двух параллельных прямых.

7) y² + a² = 0 – уравнение двух “мнимых” параллельных прямых.

8) y² = 0 – пара совпадающих прямых.

9) (x – a)² + (y – b)² = R² – уравнение окружности.

Окружность.

Определение. Окружностью называется множество всех точек плоскости, находящихся на одинаковом расстоянии, называемом радиусом, от фиксированной точки, называемой центром окружности.

 

Выведем уравнение окружности ради­уса R с центром в точке С(х₀, у₀). Для любой точки М(х, у) окружности имеем СМ = R или СМ² = R². Отсюда и получаем уравнение окружности:

(х — х₀)² + (у — у₀)² = = R². (3.1)

Если центр окружности расположен в начале координат, т.е. х₀ – 0, у₀= 0, то уравнение окружности имеет простейший вид и называется каноническим:

x² + y² = R². (3.2)

Пример. Найти координаты центра и радиус окружности, если ее уравнение задано в виде:

2x² + 2y² – 8x + 5y – 4 = 0.

 

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду, указанному выше в п.9. Для этого выделим полные квадраты:

 

Эллипс.

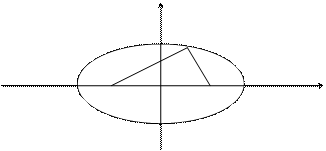
Определение. Эллипсом называется множество всех точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2 а.

у

 

М

r₁

r₂

F₁ O F₂ х

 

F₁, F₂ – фокусы. F₁ = (-c; 0); F₂(c; 0)

Для любой точки М(х, у) эллипса расстояния до фокусов есть

По определению эллипса r₁ + r₂ = 2a

После возведения в квадрат и приведения подобных слагаемых:

Если а = с, то последнее уравнение дает у = 0 — уравнение отрезка [F₁, F₂]. Если же а > с, то, обозначив а² - с² = b² (а < с < b) и разделив на а²b², получим каноническое уравнение эллипса

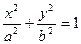, (3.3)

при этом а² - с² = b².

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Согласно этому уравнению, эллипс симметричен относительно осей координат. Положительные числа a, b называются большой и малой полуосями эллипса.

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

е = с/a. (3.4)

Т.к. с < a, то е < 1.

При е = 0 имеем: а = b, с = 0 и эллипс превращается в окружность радиуса а. При е = 1 имеем: а = с, b = 0 и эллипс вырождается в отрезок [F_1, F₂].

Если для точки М(х₁, у₁) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне эллипса.

Теорема. Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:

r₁ = a – ex, r₂ = a + ex.

 

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением:

 

1) Координаты нижней вершины: x = 0; y² = 16; y = -4.

2) Координаты левого фокуса: c² = a² – b² = 25 – 16 = 9; c = 3; F₂(-3; 0).

3) Уравнение прямой, проходящей через две точки:

 

Пример. Составить уравнение эллипса, если его фокусы F ₁(0; 0), F₂ (1; 1), большая ось равна 2.

 

Гипербола.

 

Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

y

 

M(x, y)

b

r₁

r₂

x

 

F₁ a F₂

 

c

 

 

По определению ï r₁ – r₂ ï= 2 a. F₁, F₂ – фокусы гиперболы. F₁F₂ = 2c.

Выберем на гиперболе произвольную точку М(х, у). Тогда:

обозначим с² – а² = b² (геометрически эта величина – меньшая полуось)

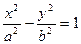(3.5)

Получили каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2 а называется действительной осью гиперболы.

Ось 2 b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых (3.6)

Определение. Отношение называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с² – а² = b²:

Если а = b, e = 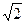, то гипербола называется равнобочной (равносторонней).

 

Пример. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса .

Для эллипса: c² = a² – b².

Для гиперболы: c² = a² + b².

 

 

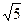
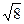
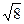
Уравнение гиперболы: .

 

Пример. Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением

 

Парабола.

Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

 

Расположим начало координат посередине между фокусом и директрисой.

 

у

А М(х, у)

 

О F x

p/2 p/2

 

 

Величина р (расстояние от фокуса до директрисы) называется параметром параболы. Выведем каноническое уравнение параболы.

Из геометрических соотношений: AM = MF; AM = x + p/2;

MF² = y² + (x – p/2)²

(x + p/2)² = y² + (x – p/2)²

x² +xp + p²/4 = y² + x² – xp + p²/4

y² = 2px (3.7)

 

Уравнение директрисы: x = -p/2, координаты фокуса F(p/2;0), центр параболы находится в начале координат. Ось симметрии – ось Ох, ветви параболы направлены в положительном направлении оси Ох ( вправо ).

Пучок лучей с источником, расположенном в фокусе, после отражения от параболы обратится в параллельный пучок лучей. На этом принципе построены параболические зеркальные антены.

В зависимости от выбора положения точки начала отсчета и осей координат относительно фокуса и директрисы можно получить еще три канонических уравнения параболы:

y² = -2px: координаты фокуса F(-p/2;0), центр параболы находится в начале координат. Ось симметрии – ось Ох, ветви параболы направлены в отрицательном направлении оси Ох (влево).

х² = 2pу: координаты фокуса F(0;p/2), центр параболы находится в начале координат. Ось симметрии – ось Оу, ветви параболы направлены в положительном направлении оси Оу (вверх).

х² = -2pу: координаты фокуса F(0;-p/2), центр параболы находится в начале координат. Ось симметрии – ось Оу, ветви параболы направлены в отрицательном направлении оси Оу (вниз).

Однако чаще приходится иметь дело с обычным уравнением параболы, известным из школы:

y = ax²+ bx + c (3.8), где a, b,c – параметры параболы. Графики при различных значениях этих параметров:

 

 

Y

a < 0

 

 

 

O X

 

 

Y

 

 

O X

 

 

a > 0

 

Обычно для построения графика параболы используют несколько ключевых моментов: корни, ось симметрии, вершина параболы, куда (вверх или вниз) направлены ветви параболы и т.п. Предполагается, что нахождение этих ключевых моментов из уравнения параболы

Пример. На параболе у² = 8х найти точку, расстояние которой от директрисы равно 4.

Из уравнения параболы получаем, что р = 4.

r = x + p/2 = 4; следовательно:

x = 2; y² = 16; y = ±4. Искомые точки: M₁ (2; 4), M₂ (2; -4).

 

Системы координат.

Любая точка на плоскости может быть однозначно определена при помощи различных координатных систем, выбор которых определяется различными факторами.

Способ задания начальных условий для решения какой – либо конкретной практической задачи может определить выбор той или иной системы координат. Для удобства проведения вычислений часто предпочтительнее использовать системы координат, отличные от декартовой прямоугольной системы. Кроме того, наглядность представления окончательного ответа зачастую тоже сильно зависит от выбора системы координат.

Рассмотрим так называемую полярную систему координат; она весьма удобна и используется довольно часто.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: