Полярная система координат.

Полярная система координат определяется заданием некоторой точки О, называемой полюсом, исходящего из точки луча l, называемого полярной осью, и масштаба для измерения длин. Кроме того, при задании полярной системы должно быть сказано, какие повороты вокруг точки О считаются положительными. Обычно считают положительными повороты против часовой стрелки.

Определение. Точка О называется полюсом, а луч l – полярной осью.

Суть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол j называется полярным углом.

 

М

 

r

r =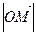

 

j

l

Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.

Тогда координаты произвольной точки в двух различных системах координат связываются соотношениями:

x = rcosj; y = rsinj; x² + y² = r²

 

Пример. Уравнение кривой в полярной системе координат имеет вид:

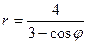. Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.

 

Воспользуемся связью декартовой прямоугольной и полярной системы координат: ;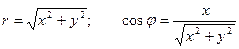

 

 

Получили каноническое уравнение эллипса. Из уравнения видно, что центр эллипса сдвинут вдоль оси Ох на 1/2 вправо, большая полуось a равна 3/2, меньшая полуось b равна 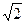, половина расстояния между фокусами равно с = = 1/2. Эксцентриситет равен е = с/a = 1/3. Фокусы F₁(0; 0) и F₂(1; 0).

y

 

 

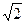
F₁ F₂

-1 0 ½ 1 2 x

 

-

 

 

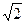
Пример. Уравнение кривой в полярной системе координат имеет вид:

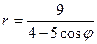. Найти уравнение кривой в декартовой прямоугольной системе координат, определит тип кривой, найти фокусы и эксцентриситет. Схематично построить кривую.

 

Подставим в заданное уравнение формулы, связывающие полярную и декартову прямоугольную системы координат.

 

Получили каноническое уравнение гиперболы. Из уравнения видно, что гипербола сдвинута вдоль оси Ох на 5 влево, большая полуось а равна 4, меньшая полуось b равна 3, откуда получаем c² = a² + b²; c = 5; e = c/a = 5/4.

Фокусы F₁(-10; 0), F₂(0; 0).

 

Построим график этой гиперболы.

 

y

 

 

 

F₁ -9 -5 -1 0 F₂ x

 

 

-3

 

Аналитическая геометрия в пространстве.

Уравнение поверхности и линии в пространстве.

Определение. Пусть в прямоугольной системе координат OXYZ координаты x, y, z связаны уравнением F(x,y,z) = 0 (1.1).

Любое уравнение, связывающее координаты x, y, z (1.1.), является уравнением поверхности S в заданной системе координат, если ему удовлетворяют координаты любой точки M(x,y,z), принадлежащей S и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.

 

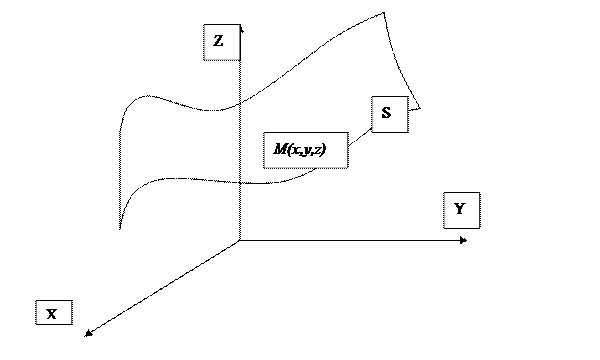
Линию в пространстве L можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением.

Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.

Тогда систему двух уравнений

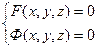
назовем уравнением линии L в пространстве.

 

Плоскость в пространстве.

Пусть Р – произвольная плоскость в пространстве. Точка М₀(x₀, y₀, z₀) Î Р. Вектор 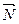= (A,B,C) –ненулевой вектор, перпендикулярный плоскости Р (нормальный вектор плоскости)

Необходимо получить уравнение плоскости.

Решение.

Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор 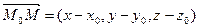. Т.к. вектор 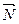- вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору 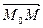. Тогда скалярное произведение

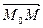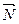× = 0

Таким образом, получаем уравнение плоскости

(5.1)

Уравнение (5.1) называют уравнением плоскости, проходящей через заданную точку.

Легко показать, что уравнение (5.1) приводится к виду:

Ax + By + Cz + D = 0 – уравнение 1-ой степени относительно переменных координат х, у, z (D = -Ax₀ – By₀ – Cz₀).

Определение. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению:

Ax + By + Cz + D = 0, (5.2)

 

где А, В, С – координаты вектора 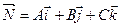- вектор нормали к плоскости.

Рассмотрим особенности расположения плоскости в тех случаях, когда те или иные коэффициенты уравнения (5.2) обращаются в нуль.

Частные случаи общего уравнения плоскости:

1. D = 0: Ax + By + Cz = 0– уравнение плоскости, проходящей через начало координат
2. А = 0: By + Cz + D = 0 – уравнение плоскости, параллельной оси ОХ, т.к. нормальный вектор 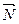= (0,B,C) – перпендикулярен оси ОХ (его проекция на ось ОХ равна нулю). Аналогично при
• В = 0: Ax + Cz + D = 0 – плоскость параллельна оси Оу
• С = 0: Ax + By + D = 0– плоскость параллельна оси Оz
3. А = D = 0: By + Cz = 0 – уравнение плоскости, проходящей через ось Ох, поскольку она параллельна оси Ох (А=0) и проходит через начало координат (D=0). Аналогично при
• В = D = 0: Ax + Cz = 0 – плоскость проходит через ось Оу
• С = D = 0: Ax + By = 0 – плоскость проходит через ось Oz
4. А = В = 0: Cz + D = 0– уравнение плоскости, параллельной координатной плоскости хОу, поскольку она параллельна осям Ох (А=0) и Оy (В=0). Аналогично:
• А = С = 0: By + D = 0 – уравнение плоскости, параллельной координатной плоскости хОz
• В = С = 0: Ax + D = 0 – уравнение плоскости, параллельной координатной плоскости yOz.
5. А = В = D = 0: Cz = 0 (z = 0) – уравнение координатной плоскости хОу, т.к. она параллельна плоскости хОу (А = В = 0) и проходит через начало координат (D=0). Аналогично при
• А = С = D = 0: By = 0 (y = 0) – плоскость совпадает с плоскостью xOz
• В = С = D = 0: Ax = 0 (x = 0)– плоскость совпадает с плоскостью yOz

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: