Определение определенного интеграла.

Пусть функция y=f(x) определена и непрерывна на отрезке [a, b], a < b.

Выполним следующие действия:

1. Точками 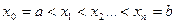разобьем отрезок [a, b] на n частичных отрезков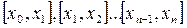

X

a=x₀ x1 x2 xi-1 xi b=x_n

 

2. На каждом частичном отрезке выберем произвольную точку c_i Î [ x_i-1; x_i ]и вычислим значения функции f(с_i).

3. Умножим найденные значения функции f(c_i) на длину соответствующего единичного отрезка Dx_i = x_i – x_i-1. Т.е. получим произведение: f(c_i)Dx_i.

4. Просуммируем полученные произведения. Получим 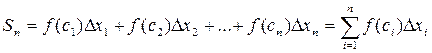(1)

Полученную сумму (1) называют интегральной суммой функции y=f(x) на отрезке [a, b].

5. Обозначим через λ длину наибольшего частичного отрезка: λ=max{ } (i=1, 2..n).

λ - шаг разбиения.

6. Перейдем к пределу интегральной суммы (1) при l ® ¥ (при этом n ® ¥):

(2)

Если предел (2) существует, то он называется определенным интегралом функции y=f(x) на отрезке [a, b] и обозначается

Определение. Определенным интегралом называется число, равное пределу интегральной суммы при шаге разбиения l ® 0, если этот предел не зависит ни от способа разбиения отрезка [a, b] на частичные отрезка ни от выбора внутренних точек сi.

Таким образом, согласно определению: 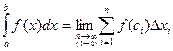(3). Сама функция f(x) при этом называется интегрируемой на отрезке [a, b].

Числа a и b называются соответственно нижним и верхним пределами интегрирования; f(x) – подинтегральной функцией; f(x)dx – подинтегральным выражением; x – переменной интегрирования; отрезок [a,b] – областью (отрезком) интегрирования.

При фиксированных пределах интегрирования a и b определенный интеграл (3) есть постоянное число. Определение определенного интеграла при помощи схемы 1. – 6. принадлежит Римману, поэтому интеграл (3) называется риммановым. Существуют и другие конструкции интегралов. Нам они не понадобятся.

Сформулируем теорему существования определенного интеграла:

Теорема (Коши). Если функция f(x) непрерывна на отрезке [ a, b ], то она интегрируема на этом отрезке, т.е. определенный интеграл существует.

 

Некоторые свойства определенного интеграла, следующие непосредственно из его определения (3):

 

1. Определенный интеграл не зависит от обозначения переменной интегрирования:

 

1. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

.

 

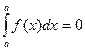3. Если подинтегральная функция равна единице, то определенный интеграл этой функции по отрезку [a,b] равен длине этого отрезка, т.е.:

.

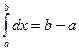Геометрический смысл определенного интеграла.

Пусть на отрезке [a,b] задана непрерывная функция y = f(x) ³ 0. Фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, сбоку прямыми x = a и x = b, называется криволинейной трапецией.

y

y = f(x)

 

 

0 x

 

Найдем площадь этой трапеции S.

Если функция f(x) ³ 0 на отрезке [a,b], тогда интегральная сумма

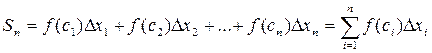(1) геометрически представляет собой площадь ступенчатой фигуры S_n:

y

 

 

0 a c₁x₁ c₂x₂ x_i-1 c_i x_i x_n-1c_n b x

Площадь криволинейной трапеции S приближенно равна площади ступенчатой фигуры:

.

С уменьшением всех величин Dx_i точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличивается. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры S_n при неограниченном возрастании n ® ¥ так, что l ® 0:

.

Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции. В этом и состоит геометрический смысл определенного интеграла.

 

Формула Ньютона-Лейбница.

Пусть функция y = f(x) интегрируема на отрезке [ a, b ].

Теорема. Если функция y = f(x) непрерывна на отрезке [ a, b ] и F(x) какая-либо ее первообразная на этом отрезке (F¢ (x)= f(x)), то имеет место формула

(1).

Доказательство:

Точками 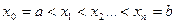разобьем отрезок [a, b] на n частичных отрезков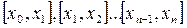

x

a=x₀ x1 x2 xi-1 xi b=x_n

Рассмотрим тождество: F(b) – F(a) = F(x_n) – F(x₀) = (F(x_n) – F(x_n-1)) + (F(x_n-1 – F(x_n-2)) +... +(F(x₁) – F(x₀)).

К каждой разности в скобках применим формулу Лагранжа: f(b) – f(a) = f¢ (c)×(b – a).

Получим:

F(b) – F(a) = F¢ (c_n)(x_n – x_n-1) + F¢ (c_n-1)(x_n-1 – x_n-2) +...+ F¢ (c₂)(x₂ – x₁) + F¢ (c₁)(x₁ – x₀) =

_{n n n}

å F¢ (c_i)(x_i – x_i-1) = å f(c_i)(x_i – x_i-1), т. е. F(b) – F(a) = å f(c_i)(x_i – x_i-1) (2), где c_i – некоторая ^{I=1 I=1 I=1}

точка интервала (x_i-1; x_i). Т. к. функция y = f(x) непрерывна на [ a, b ], то она интегрируема на этом отрезке. Поэтому существует предел интегральной суммы, равный определенному интегралу от f(x) на отрезке [ a, b ].

Перейдем в равенстве (2) к пределу при n ® ¥ (l ® 0), получим , т. е. . Ч.т.д.

Равенство (1) называется формулой Ньютона-Лейбница.

_b

Разность F(b) – F(a) обозначают следующим образом: F(x) ç _a и формулу (1) в этом случае можно переписать

.

Формула (1) дает удобный способ вычисления определенного интеграла:

- надо найти первообразную подинтегральной функции – F(x);

- посчитать разность значений этой первообразной на концах отрезка [ a, b ] – F(b) – F(a).

Примеры.

1). ;

2). .

 

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: