Технологических процессов выполнения работ

1.2.1. Проверка принадлежности к нормальному закону

распределения

Показатели и параметры технологических процессов изготовления, сборки, монтажа и испытаний изделий судового машиностроения могут иметь различное распределение: нормальное, равномерное, экспоненциальное и др.

Установление принадлежности данных ТП к тому или иному закону распределения выполняется на основе закона Пирсона (χ²).

Наиболее часто требуется установить принадлежность наблюдаемых значений случайно величины {X} к нормальному закону распределения, где {X} – значения технологических параметров (точность обработки, достигнутая чистота обработанной поверхности, величина зазора и т.д.).

При этом в результате измерений может быть получен точечный ряд наблюдений и систематизированный ряд, когда наблюдения (измерения) могут быть разбиты на ряд подинтервалов, в каждый из которых попадает случайное число наблюдений (измерений) – m; где i=1n – число наблюдений или число интервалов, на которые разбиты наблюдения (при большом n).

Итак, проверка принадлежности рассматриваемого наблюдения к нормальному закону распределения () выполняется на основе двух критериев для числа наблюдений n≤50.

Критерий 1. Вычисляется параметр наблюдения:

где – порядковый номер наблюдений; x_i– значение случайной величины;

Вычисленное значение d должно удовлетворять условию

или

 

где , –нижнее и верхнее граничные значения параметров нормального распределения. Определяются по справочной таблицеП-4 [9], для уровня значимости q = 1, 2, 5, 10.

Если условия (3) или (4) выполнены, то гипотеза принадлежности x_i к нормальному закону ()не отвергается.

Критерий 2. Используется для проверки концов рассматриваемом наблюдении не более m разностей превосходят значение ,

, (5)

где - верхняя – процентная квантиль нормированной функции Лапласа, определяется для

по справочным таблицам[9]:

,

Значение m, полученное по результатам анализа наблюденных значений x_i и сравнению по условию (5), не должно превосходить предельное значение m^*.

где m^* определяется по справочным данным таблицы П-5 [9]для заданных значений (6) и n.

Если условие (8) выполняется, то гипотеза принимается.

Пример. Проверить по данным наблюденных значений времени на отказ (x_i = T_oi, ч) принадлежность к нормальному закону распределения значения T_oi (). Данные для анализа в таблице 3.

Таблица 3

i	Toi, ч	i	Toi, ч	i	Toi, ч

Построить гистограмму α (t) для данных таблицы 3.

 

 

1.2.2. Пример оценки принадлежности результатов обработки детали к нормальному закону распределения

Результаты обработки детали к нормальному закону распределения будут выглядеть следующим образом:

,

где – отклонение наружного размера обрабатываемых деталей от номинала, мкм; - обозначение нормального закона распределения.

N_дет= 100 шт. – число обработанных деталей;

Предельно допустимые размеры:

Ø_max =114,955 мм. – A₁₀^max

Ø_min =114,919 мм. – A₁₀^min

Допуск на обработку:

δ=36мкм.

Предельно допустимые отклонения:

x_i^max =115-114,955=-45мкм,

x_i^min =115-114,919=-81мкм,

где x_i^max – максимальное предельное отклонение; x_i^min – минимальное предельное отклонение.

Данные измерений результатов обработки Ø115 мм приведены в таблице 4.

 

Таблица 4

Систематизированные результаты измерения

i	xi , интервалы отклонений, мкм	mi, число деталей	, середина интервала, мкм	qi, отклонения от номинального размера, мкм
от	до
	-81	-77		-79	0,05
	-77	-73		-75	0,06
	-73	-69		-71	0,08
	-69	-65		-67	0,1
	-65	-61		-63	0,2
	-61	-57		-59	0,21
	-57	-53		-55	0,16
	-53	-49		-51	0,1
	-49	-45		-47	0,01
			1,0

Порядковый номер интервала:

;

m_i – число деталей попавших в i- тый интервал.

Рассчитаем значение σ(x)–среднее квадратичное значение отклонения для наблюденных значений x_i (таблица 4).

При отсутствии систематической погрешности при обработке:

– когда центр группирования совпадает с координатой поля допуска ∆₀; (9)

При наличии систематической погрешности при обработке:

где ∆_сист – систематическая погрешность обработки; σ(x) – среднеквадратичное отклонение наблюденных значений x_i.

Разбивка на интервалы представлена на рисунке 1, где Δx–длина подинтервала, который может быть одинаковым. Количество же интервалов зависит от размеров выборки, обычно N_инт 6…10.

Δx

Amin

Amax

Рис.1. Интервалы рассеяния размера А.

На рисунке 2 представлена гистограмма распределения (функция плотности вероятности q_i) наблюдений величины x_i.

qi i

0,05

0,06

0,08

0,1

0,2

0,21

0,16

0,1

0,04

0,05

0,1

0,15

0,2

0,25

Рис.2. Гистограмма функции плотности вероятности q_i, построенная по данным таблицы 4.

Проверим принадлежность рассматриваемого наблюдения к нормальному закону распределения.

Рассчитаем среднее значение наблюдений для систематизированного ряда наблюдений:

где - среднее подинтервала; N– число поддиапазонов.

Критерий 1 (3).

.

Для систематизированного ряда:

где

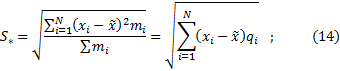
- среднеквадратичное отклонение среднеарифметического;

- середина подинтервала;

- среднее наблюденных значений.

Среднее квадратичное отклонение x_i для систематизированного ряда:

где - середина подинтервала; - среднее наблюденных значений; – число подинтервалов.

Расчеты для проверки критерия 1 (3) исполнены на основе [11], [12], [13]и выполняются в MSExcel;

d =0,808725;

d_н =0,66 (табл. приложения 3);

d_н =0,66 (табл. приложения 3);

;

.

Условия Критерия 1 (3) выполнены.

Проверка Критерия 2 по (5) и (9) и данным таблиц [9].

Разностей – нет;

(q= 0,02 –уровень значимости)(табл. П-1[9]);

Условия Критерия 2 выполнены.

Гипотеза принимается. Условие (9) выполнено, систематическая погрешность отсутствует:

 

 

1.2.3. Проверка однородности наблюдений

1.2.3.1.Проверка допустимости отличий между оценками дисперсий для двух групп наблюдений

(с использованием критерия Р.Фишера)

где > - несмещённые оценки дисперсий, вычисленные для I и II групп наблюдений с выражением;

где n₁ – число наблюдений в I группе; n₂ – число наблюдений во II группе.

Группы наблюдений могут отличаться условиями или временем выполнения работ.

- табличное значения критерия Фишера, определяемое по данным таблиц приложения 4 для уровня значимости q=0,01 (0,05), F_0,01;k₁;k₂ (F_0,01;k₁;k₂), где

– число степенейсвободы числителя;

- число степеней свободы знаменателя.

Гипотеза допустимости отличий принимается, если

 

 

1.2.3.2.Проверка допустимости отличий средних

арифметических для двух групп наблюдений

Обозначим , , n₁ данные оценок среднего арифметического, дисперсии и числа наблюдений для I группы. То же для II группы , , n₂.

Оценим дисперсию разности средних арифметических:

Различие между средними арифметическим считается допустимым, если выполняется условие:

где

– 100 квантиль нормированной функции Лапласа (6) (табл. П-1 [9]).

Пример. Для данных наблюдений по таблице проверить допустимость отличий дисперсий и средних арифметических.Пример выполнить студентам самостоятельно.

Таблица 5

i	Toi, ч	i	Toi, ч	i	Toi, ч	i	Toi, ч	i	Toi, ч

Обозначения в таблице 5: i– порядковый номер наблюдения; T_oi – основное время выполнения работ, ч.

1.2.4. Проверка грубых выбросов

Если в группе наблюдений есть 1-2 наблюдения, резко отличающиеся от остальных, следует оценить статистическим методом, являются ли эти отличия грубыми ошибками. Для проверки определяется табулированное значение:

и

Определяется табличное значение , для n -числа наблюдений и уровня значимости q.

Вычисляются по данным наблюдений:

где

– среднеквадратичное отклонение x_i (7);

n – число наблюдений;

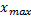- максимальное значение контролируемой величины;

Если

то отбрасывать наблюденное значение 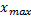как грубую ошибку нельзя. В противном случае исходную статистику следует корректировать, пересчитав значения и .

Пример. Определить по данным таблицы 5, имеется ли грубый выброс.Пример выполняется студентами самостоятельно.

 

1.2.5. Доверительные интервалы

Получив оценку значения случайной величины А, представляет интерес выяснить, в каких пределах она может изменяться при повторных наблюдениях.

Доверительный интервал – интервал, который с заданной вероятностью (называемой доверительной) накрывает истинное значение величины А.

Доверительный интервал

отвечает доверительной вероятности

где - процентная точка распределения Стьюдента (табл. П-7 [9]); определяется по числу степеней свободы и уровню значимости q; – оценка среднеквадратического отклонения среднего арифметического:

Для случая нормального распределения доверительный интервал определяется следующим образом:

Пример. Определить по данным таблицы 5 доверительный интервал для наблюденных значений T_oi. Пример выполняется студентами самостоятельно.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: