 |
Значений конструктивно-технологических параметров изделий судового машиностроения
|
|
|
|
1.3.1. Анализа связей показателей технологической
трудоёмкости с классификационными, конструктивно-технологическими параметрами и особенностями
судовых заказов
Алгоритм анализа включает следующие действия:
1)Составление таблицы исходных данных.
Форма таблицы исходных данных представлена на рис.1.
| Номер объекта наблюдения (i) | Значения показателей технологической трудоёмкости | Значения классификационных, конструктивно-технологических параметров и особенностей судовых заказов | |||||||
| у∑ | у1 | у2 | … | уm | х1 | х2 | … | хк | |
| … | |||||||||
| n |
Рис.3. Форма таблицы исходных данных.
Обозначенияна рис.1: у∑, у1, у2 … уm – значения технологической трудоёмкости работ, нормо-ч; у∑ = у1 + у2 +…..+ уm; х1, х2, х3,…, хк – значения КТП (в физических величинах или принятых числовых кодах).
Требования к заполнению таблицы исходных данных:
· таблица должна иметь полный ранг, т.е. не иметь пропусков данных. Интерполяция и экстраполяция данных не допускается.
· номенклатура КТП, включённых в таблицу, не ограничивается;
· декомпозиция показателей трудоёмкости определяется потребностью в получении оценок.
2)Расчёт значений парных коэффициентов корреляции.
Значения парных коэффициентов корреляции показывают наличие и степень тесноты статистической линейной (нелинейной) связи, что положено в основу выдвижения гипотез о виде математических моделей оценки показателей трудоёмкости от значений КТП, включая временной параметр.
Расчёт значений парных коэффициентов корреляции производится по формуле:
|
|
|
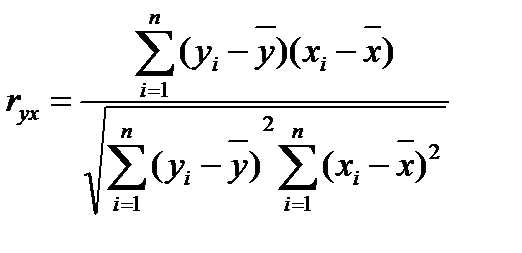 , (31)
, (31)
где:


Значения  лежат в пределах
лежат в пределах  .
.
а) При значении  - связь сильная, возможен расчет линейной регрессионной зависимости оценки показателя трудоёмкости вида:
- связь сильная, возможен расчет линейной регрессионной зависимости оценки показателя трудоёмкости вида:

где ŷ – оценка показателя трудоёмкости; bo, b1 – оценки математической модели линейной регрессии вида (31).
б) При значении  - связь на фоне ошибки; требуется подбор наилучшей нелинейной модели множественной регрессии вида:
- связь на фоне ошибки; требуется подбор наилучшей нелинейной модели множественной регрессии вида:


Линеаризованное (34)


Линеаризованное (36)

в) При значении  - слабая связь (ошибка) или нелинейность.
- слабая связь (ошибка) или нелинейность.
Необходим поиск наилучших нелинейных зависимостей вида (33), (34), (36), адекватных условиям производства.
3)Рассчитанные значения парных коэффициентов корреляции удобно представить матрицами |Ф1| и |Ф2|:


где у ф – фактическое значение трудоёмкости работ (в абсолютном или относительном выражении).
Отметим, что
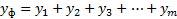 .
.
Рассчитанные значения парных коэффициентов корреляции дают полную картину связей для разработки параметрических и временных зависимостей оценки показателей трудоёмкости.
Пример поиска и расчёта математических моделей оценки трудоёмкости строительства судовых заказов и составляющих трудоёмкости по укрупнённым видам работ представлен в разделе 2.
1.3.2. Синтез математических моделей оценки показателей
трудоёмкости
Синтез математических моделей оценки показателей трудоёмкости предполагает поиск наилучших моделей с расчётом значений коэффициентов b o, b 1, b 2,…, обеспечивающих наилучшие предсказывающие свойства рассчитанных моделей и адекватных условиям производства.
Расчёт математических моделей выполняется на основе метода наименьших квадратов (МНК), обеспечивающего наилучшее приближение расчетного значения показателя трудоёмкости к истинному.
Для расчёта значений коэффициентов bo, b1, b2… составляется и решается система МНК – уравнений вида:
|
|
|
 , (37)
, (37)
где Гауссовы суммы:
[ x 1]= 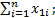 [ x 2]=
[ x 2]=  [ x к]=
[ x к]= 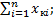
[ y ]=  [ x 1 y ]=
[ x 1 y ]=  [ x 2 y ]=
[ x 2 y ]= 
 =
=  и т.д.
и т.д.
Для линейных и линеаризованных однопараметрических уравнений расчет зависимостей (32), (35) выполняется также на основе МНК:
 , (38)
, (38)
где Гауссовы суммы:

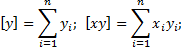
В результате решения системы МНК-уравнений (37), (38) должны быть определены значения коэффициентов b o, b 1,…, b к.
1.3.3. Проверка соответствия рассчитанных моделей
статистическим критериям в обеспечение
адекватности условиям производства.
Адекватность и достоверность рассчитываемых моделей условиям производства работ определяется, с одной стороны, использованием значений фактических затрат труда на выполнения работ, например по ранее построенным судовым заказам (рассчитываются регрессионные модели оценки); с другой стороны, рассчитываемые модели должны содержать определяющие параметры, известные на момент получения оценок и удовлетворять ниже перечисленным критериям:
· несмещённости;
· эффективности;
· состоятельности.
Для решения сформулированной задачи определяется расчётное значение ŷ в соответствии с рассчитанной зависимостью, далее:
· выполняется расчёт и анализ остатков;
· построение и анализ графиков остатков (ошибки предсказания);
· оценивается эффективность модели по виду графика остатков и расчётному значению среднеквадратичного отклонения остатков от среднего арифметического;
· рассчитывается значение множественного коэффициента корреляции (для линейных регрессионных моделей) или значение корреляционного отношения (для нелинейных регрессионных моделей);
· оценивается погрешность предсказания при использовании модели;
· оценивается статистическая значимость модели по критерию Фишера (для линейных регрессионных моделей).
1.3.3.1. Алгоритм оценки статистических критериев для
рассчитанных моделей
1)Расчёт и анализ остатков.
Остаток – это разность между фактическим и расчётным значением показателя, определяемый по формуле:

Графики остатков:
 – общий;
– общий;
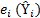 – от расчётного значения;
– от расчётного значения;
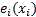 – от параметра.
– от параметра.
2)Проверка несмещенности выполняется в соответствии с выражением:

Одновременно проверяется средний остаток:

Возможный вид графиков остатков (рис.4) выявляет отклонения от нормального поведения ошибки:
|
|
|
а) eiσ (e)=Const
ē = 0 yi
Рис.4. График остатков.
График остатков (рис.4 а)не выявляет отклоненийот нормального поведения ошибки. С увеличением значения предсказываемого параметра погрешность не увеличивается (σ (е) = Const).
График остатков – точечный. Заштрихованное поле – расположение точек графика остатков.
3)Проверка эффективности, выполняемая по графику остатков, заключается в расчёте и установлении требования:
 = Const; (42)
= Const; (42)
б) ei σ [e] ≠ Const
ē = 0уi
Рис.4. Модель требует корректировки на нелинейность.
Поиск нелинейных моделей, адекватных условиям производства – творческая задача, которая решена в разделе 2.
4)Расчет значения множественного коэффициента корреляции для линейных моделей
Значение множественного коэффициента корреляции определяется выражением:
 ; (43)
; (43)
где:

0,8 ≤ R ≤ 1,0 для значимых моделей оценки;
Погрешность использования модели:
 . (44)
. (44)
Для однопараметрических линейных моделей R = ryx. Условие используется для установления значимости модели и проверки результатов расчёта указанных моделей.
5)Оценка корреляционного отношения
Значение корреляционного отношения требуется только для нелинейных моделей с целью определения их значимости и адекватности условиям производства.
Корреляционное отношение для нелинейных моделей определяется на основе зависимостей:
ϱ 1 =  , (45)
, (45)
где:
 =
=  ;
;  =
=  ;(46)
;(46)
или:
ϱ 2 =  , (47)
, (47)
где  - фактическое значение трудоёмкости, нормо-ч;
- фактическое значение трудоёмкости, нормо-ч;  =
=  - среднее значение трудоёмкости, нормо-ч;
- среднее значение трудоёмкости, нормо-ч;  – расчётное значение трудоёмкости, полученное при использовании регрессионной зависимости.
– расчётное значение трудоёмкости, полученное при использовании регрессионной зависимости.
Для значимых нелинейных зависимостей:
0,5 ≤ ϱ 1 ≤ 1; 0,5 ≤ ϱ 2 ≤ 1
Определяется сочетанием значений указанных величин, приближающих полученную при использовании нелинейных моделей оценку к максимальному приближению к истинному значению оцениваемого показателя.
6) Расчет статистической значимости модели (на основе коэффициента Фишера).
Расчётное значение коэффициента Фишера определяется выражением:
|
|
|


где p = 1 – число параметров в модели вида (32), (35), SSрегр.(43.1); n- число наблюдений.

Fрасч. ≥ Fтабл.q - критерий статистической значимости модели
k1 = p; k2 = n-2p,
где q = 0,01; (0,05) – уровень значимости; k1 – число степеней свободы числителя; k2 – число степеней свободы знаменателя; Fтабл. – определяется по справочным таблицам.
Рассчитанные математические модели оценки показателей трудоёмкости, удовлетворяющие изложенным критериям, дают достоверную оценку, адекватную условиям производства.
7)Число значимых цифр в процессе расчёта моделей оценки показателей трудоёмкости должно быть не меньше числа значимых цифр исходных данных, но должно превышать указанное значение с учётом нелинейности преобразований на 1-2 знака.
|
|
|


