Приложения синергетики в гуманитарных науках

ПРИЛОЖЕНИЯ СИНЕРГЕТИКИ В ГУМАНИТАРНЫХ НАУКАХ

Приложения теории катастроф и теории бифуркации к жизненным ситуациям

Вся тайна и очарование процессов, приводящих к качественному перерождению старой системы, сосредоточены как раз в той критической точке, когда это самое перерождение и происходит. Если мы поставили своей целью разобраться, как это отдельным личностям удается генерировать решения, выводящие обычные объекты и ситуации на качественно иные уровни, то нам прежде всего необходимо разобраться с этим самым критическим моментом.

Выше уже говорилось о катастрофах, происходящих с упругими несущими конструкциями. Продемонстрировать это может простая школьная резинка - ластик, подойдет также пружинка от шариковой ручки. Что произойдет, если слегка нада­вить отобранный предмет? Понятно, что резинка, пружинка сожмется и ответит сопротивлением - упругой силой. Если сдавить сильнее? Сожмет­ся еще больше, и упругая сила сопро­тивления тоже увеличится. А если еще сильнее? Вроде бы ничего нового не произойдет - чем больше деформация, тем больше сила упругости. Однако, здесь и подстерегает нас сюрприз! Кто-то уже понял, наверное, что пружинка может вдруг выпрыгнуть из наших пальцев. Действительно! В некоторый момент резинка (пружинка) вдруг (совершенно внезапно! ) начинают вести себя совсем не так, как мы могли бы ожидать: резинка вдруг изгибается посередине, почти складывается пополам, выпучивается и остается в таком состоянии (рисунок).

Если мы попытаемся и дальше увеличивать давление, то обнаружим, что ощущаем гораздо меньшую силу сопротивления: резинка САМА изменила свою форму так, чтобы при том же сжатии пальцев воспринять от нас меньше энергии, чем раньше!

Однако, наш «катаклизм» обратим: мы можем разжать пальцы и резинка примет исходную форму. Но если бы мы взяли объект из менее эластичного материала - например, спичку, то катастрофа вполне оправдала бы свое название: спичка бы держала нагрузку до определенного момента, после чего она бы просто сломалась, поскольку материал ее не в силах выдерживать такие деформации, как резина. Понятно, что, если все это происходило бы, например, с колонной здания, то катастрофа случилась бы совсем не игрушечная, а самая настоящая…

Если нам попалась хорошая резинка и мы оказываем давление строго по ее оси, то обнаружим, что прогиб происходит то в одну, то в другую сторону: куда в каждый следующий раз прогнется резинка предсказать невозможно - это остается неожиданностью. Дело в том, что резинка в критический момент находится в неустойчивом состоянии - как, например, мяч, который мы попытаемся удержать на своей голове. После критического сжатия любое случайное малое возмущение, внешнее или внутреннее, прекращает неустойчивое состояние - резинка скачком прогибается в какую-то сторону. В какую - зависит от этого возмущения. Таким образом, влияние малых возмущений на качественное изменение объекта - очень важный момент! Обыденный опыт подсказывает нам, что большие результаты требуют, как правило, больших усилий: чтобы сдвинуть с места огромный камень, надо обладать недюжинной силой. Оказывается, однако, что иногда совсем незначительные усилия могут приводить к весьма масштабным результатам. Так, перегруженная колонна может некоторое время сохранять прямое положение, а скопившийся за зиму снег может продолжать держаться на склоне горы. Но дуновение ветра или разговор стоящих невдалеке людей нарушает хрупкое равновесие, и... вот она - катастрофа: рушится инженерное сооружение; а посёлок в горах сметает лавина. Или когда ситуация на рынке становится слишком сложной, то любой случай может привести гигантскую корпорацию к банкротству.

Попытаемся графически представить себе изменение поведения резинки при выпучивании - так называемую «поверхность состояния объекта». Зависимость угла прогиба от сжимающей силы представлена на рисунке: до некоторого усилия никакого прогиба нет совсем, и график следует из начала координат по горизонтальной оси. Начиная с некоторого критического момента, исходное неискривлённое состояние резинки остаётся возможным, но становится неустойчивым (поэтому оно показано штриховой линией), причём прогиб может произойти как в одну, так и в другую сторону (на графике - вверх или вниз), а величина его быстро увеличивается с увеличением силы сжатия.

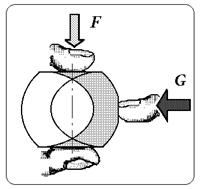Что будет происходить с резинкой, когда выпучивание уже произошло, если мы станем прилагать усилие поперек, как бы стараясь вернуть ее в исходное положение? После выпучивания резинка может иметь два различных состояния - прогиб либо в одну, либо в другую сторону (а если бы мы имели дело не с прямоугольной в сечении резинкой, а с круглой пружинкой от шариковой ручки, то число возможных состояний после выпучивания увеличилось бы до бесконечности - пружинка может выгнуться в любом направлении из 360 градусов окружности! ).

Попробуем давить на резинку со стороны выпучивания: сначала мы почувствуем нарастающее сопротивление, однако только до некоторого момента, когда опять происходит резкое и неожиданное событие: резинка вдруг " перещелкнется" - скачком прогнётся в противоположную сторону. Если теперь убрать боковое давление, то резинка все равно останется в новом состоянии. Её можно заставить перескочить обратно, но для этого потребуется прилагать поперечное давление в обратном направлении. Этот интересный эффект есть ничто иное, как Память! Резинка теперь, оказывается, запоминает направление последнего воздействия и хранит эту информацию до того времени, пока новое воздействие не перекинет её в иное положение! Таким образом, поведение обычной резинки теперь ничем не отличается от поведения ячейки памяти компьютера.

Если мы попытаемся представить себе поведение нашего объекта в трехмерном пространстве зависимости прогиба от сжимающей и поперечной изгибающей сил, то обнаружим в нем некую поверхность, похожую на сборку ткани – (рис. ¯ ).

Эта поверхность называется поверхно­стью состо­я­ния нашего объекта, то есть все возможные состояния нашей резинки являются точками этой поверхности. Поверх­ность состояния - это что-то вроде карты, которая позволяет ориентироваться в поведении объекта. Как это можно делать? Чтобы узнать, в каком состоянии будет находиться наша резинка при определен­ных внешних воздействиях, надо найти точки пересечения этого кусочка смятой ткани с плоскостями, которые соответствуют поперечным и продольным внешним силам - точка пересечения и покажет тот угол прогиба, который будет иметь место при данных воздействиях. Если окажется, что поверхность пересекается в двух местах, то при данных условиях у резинки может быть два различных состояния (прогиб либо в одну, либо в другую сторону).

Эта поверхность носит в Теории катастроф Тома название КАТАСТРОФЫ СБОРКИ - одной из семи элементарных математических катастроф. Легко можно заметить, что зависимость прогиба от сжимающего усилия представляет собой " продольный разрез" поверхности катастрофы сборки при G=0: точка состояния спокойно катится по поверхности от исходного нулевого положения, пока в некоторый момент не достигнет развилки. Теперь у неё есть выбор: покатиться на верхний лист поверхности или скатиться вниз (чисто теоретически, точка может покатиться и по среднему язычку сборки - показан штрихами; но, как мы уже понимаем, это настолько неустойчивый маршрут, что он не является реальным).

В свою очередь, эффект запоминания направления последнего поперечного воздействия (силы G) иллюстрирует " поперечный разрез" поверхности при F=const: точка устойчиво покоится либо вверху, либо внизу, пока достаточно сильное поперечное давление не подведет ее к той границе, где ей приходится прыгать или падать на другой лист поверхности.

Элементарные катастрофы более высоких порядков представляют собой гораздо сильнее " измятые" салфетки, причём существуют они в пространствах с числом измерений больше трёх, и, следовательно, не могут быть легко представлены нами. Но и не самая сложная катастрофа - трехмерная сборка, оказывается, может служить универсальной моделью, объясняющей многое!

Катастрофичные явления присущи едва ли не всякому объекту окружающего нас мира. Для описания таких процессов необходима достаточно простая модель, составленная из универсальных сущностей - в качестве таких сущностей предложим следующее:

· интересующий нас результат поведения Объекта назовем Выходом, или Продуктом,

· причину или необходимое для выхода условие назовем Входом, или Ресурсом.

· любой объект изучения может быть разделен, как минимум, на две части, потребляющие общий Ресурс, а общий Продукт складывается из продуктов его составляющих частей,

· существует некоторая зависимость количества Ресурса, поступающего на Вход каждой части, от величины её Выхода - то есть в объекте реализована некоторая Обратная связь.

 

Здесь, фактически, мы выбираем для анализа жизненных ситуаций типичную модель кибернетики: Объект, Вход, Выход, Обратная связь.

 

 

Здесь подразумевается, что:

· Объект управления никогда не является монолитным.

· Обратная связь действует таким образом, чтобы Выходы обоих составляющих элементов были равными.

· Эффективность каждого элемента, то есть отношение Выхода ко Входу нелинейно зависит от поступающих Ресурсов: недостаток Ресурса так же плох, как и избыток

 

Теперь мы готовы описать любое явление в общих терминах:

Объект	Элементы	Вход	Выход
Завод	Цеха	Материалыполуфабрикаты	Готовая Продукция
Атомный Реактор	Участки Активной Зоны	Ядерное Топливо	Тепло
Двое	Он и она	Поступки	Чувства

 

Оказывается, катастрофа органически присуща любой из приведенных выше систем! Этот неожиданный момент обнаруживается сразу, как только мы соглашаемся с тем, что любой Объект состоит из частей, потребляющих один и тот же Ресурс (зависящих от одного условия), и что Эффективность системы зависит от поступивших Ресурсов или внешних условий нелинейно. Оказывается, поверхность её состояния представляет собой уже знакомую нам катастрофу сборки. В отличие от классической катастрофы сборки, наша модель характеризуется двумя точками - по одной точке состояния на каждую составную часть (рис. ¯ ). Эти точки также всегда принадлежат поверхности состояния, но располагаются на ней не произвольно. Поперечная ось наше­го трехмерного простран­ства состояния теперь представля­ет собой соотношение Эффективностей обеих частей систе­мы: в центре поперечной оси соот­ношение равно единице (то есть оба элемента идентичны), справа находится область более эф­фективных (произ­водительных) элементов, слева - менее… Если оба элемента совершенно оди­наковы, то их точки состояния сливаются (отношение Эффективностей рав­но единице) и могут пере­мещаться вдоль поверхности строго по её середине. Если элементы неодинаковы (система неоднородна), то точки состояния должны находиться по разные стороны от середины поверхности (симметрично) - одна слева, другая справа.

В случае неоднородной системы (рис. ­) при изменении ситуации каждый элемент ведет себя по-своему: один сразу " скатывается" вниз (теряя даже то малое, что принадлежало ему вначале), а другой поднимается вверх (еще более упрочивая свою позицию). В случае однородной системы (рис. ) первоначально поведение обеих частей совершенно идентично - обе рабочие точки сливаются и перемещаются вдоль поверхности строго по ее середине, разделяя Ресурсы строго поровну между собой. Однако, в некоторый момент поведение равных элементов изменяется кардинально: один забирает все ресурсы, а другой почему-то всё теряет. Теперь нам остается только посмотреть, как реализуется внезап­ное изменение состояния на заводе, атомном реакторе, влюбленной паре и во многих других самых различных жизненных ситуациях.

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: