 |
Формальное педставление игр для случая двух игроков
|
|
|
|
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ
ЭЛЕМЕНТЫ ТЕОРИИ ИГР
Рабочая тетрадь № 2
студента_______________________________________________
факультета___________ отделения ___________группы________
Специальность 080107 «Налоги и налогообложение»
Составитель: Е.Ю. Лискина, канд. физ.-мат. наук, доцент
Рязань 2007
Тема 6. ЭЛЕМЕНТЫ ТЕОРИИ ИГР
Игровые модели и их классификация
Основные определения
Определение 1. Конфликтной ситуацией (конфликтом) будем называть явление или ситуацию, в которой участвуют две или более стороны, имеющие различные интересы и обладающие возможностями применять для достижения своих целей разнообразные действия.
Определение 2. Упрощённая формализованная модель конфликтной ситуации называется игрой.
Замечание. От реального конфликта игра отличается наличием правил игры.
Теория игр – раздел прикладной математики, занимающийся построением математических моделей возможных конфликтных ситуаций и разработкой методов решения возникающих в этих ситуациях задач.
Определение 3. Заинтересованные стороны конфликта называются игроками.
Определение 4. Каждое действие игрока в рамках правил игры и в зависимости от ситуации, сложившейся в процессе игры называется ходом или стратегией игрока.
Определение 5. Число, выражающее степень удовлетворения интересов игрока в данной ситуации, называется выигрышем игрока.
Определение 6. Зависимость величины выигрыша игрока от всевозможных стратегий называется функций выигрыша (платёжной функцией).
Определение 7. Значение функции выигрыша называется исходом игры.
Замечание. В теории игр предполагается, что функции выигрыша и множество доступных для каждого игрока стратегий известны, то есть каждый игрок знает как свои функции выигрыша и набор имеющихся в его распоряжении стратегий, так и функции выигрыша и стратегии остальных игроков. В соответствии с этой информацией он и организует своё поведение, то есть определяет выбор своей стратегии. Суть игры заключается в том, что каждый из игроков принимает такие решения, которые, как он полагает, могут обеспечить ему наилучший результат (исход).
|
|
|
Определение 8. Стратегия называется оптимальной, если она при многократном повторении обеспечивает данному игроку максимально возможный средний выигрыш.
Основные направления изучения теории игр:
1) выработка принципов оптимальности – критериев, по которым поведение игроком следует считать оптимальным;
2) выяснение реализуемости принципов оптимальности – установлению оптимальных в выработанном смысле ситуаций, отысканию их реализаций.
Определение 9. Игровая ситуация называется равновесной (равновесием), если в её нарушении не заинтересован ни один из игроков.
Замечание. Равновесие является одной из форм представления об оптимальности в игре, так как в равновесной ситуации каждый игрок получает наибольший выигрыш.
Определение 10. Если в игре существуют стратегии, приводящие к равновесной ситуации, то такие стратегии называют чистыми.
Определение 11. Если в игре не существует стратегий, приводящих к равновесной ситуации, но существуют комбинации исходных стратегий, приводящие к равновесию, то такие комбинации называют смешанными стратегиями.
Замечание. Часто смешанную стратегию представляют как случайный выбор игроками чистых стратегий, при котором случайные выборы различных игроков независимы в совокупности, а выигрыш каждого из них определяется как математическое ожидание случайного выигрыша.
Определение 12. Игра, в которой не существует равновесия, достигаемого чистыми стратегиями, но достигаемого смешанными стратегиями, называется смешанным расширением исходной игры.
|
|
|
Классификация игр
| № | Признак | Класс игр | |
| 1. | Число игроков | а | Парные игры (два игрока) |
| б | Множественные игры (три и более игрока) | ||
| в | Игры с бесконечным числом игроков | ||
| 2. | Количество стратегий | а | Конечные игры (конечное число стратегий у каждого игрока) |
| б | Бесконечные игры (бесконечное число стратегий у каждого игрока) | ||
| Свойства функции выигрыша | а | Игры с нулевой суммой или антагонистические игры (выигрыш одного игрока равен проигрышу другого) | |
| б | Игры с постоянной разностью (игроки выигрывают и проигрывают одновременно и им выгодно согласовывать свои действия) | ||
| в | Игры с ненулевой суммой (возможны и конфликты и согласованные действия) | ||
| Возможность ведения переговоров | а | Кооперативные (коалиционные) (игроки могут договариваться о совместных стратегиях) | |
| б | Некооперативные игры (игроки не имеют возможности договариваться) | ||
| Характер действий игроков | а | Позиционные игры (игроки совершают действия последовательно, друг за другом) | |
| б | Непозиционные игры (игроки действуют одновременно) |
Упражнение. Приведите примеры игр каждого класса.
Матричные игры
Формальное педставление игр для случая двух игроков
Определение 1. Игра, в которой участвуют два игрока, называется парной игрой.
Пусть в игре участвуют два игрока А и В. Каждый из игроков располагает конечным числом чистых стратегий. Обозначим их соответственно:
– стратегии первого игрока,
– стратегии второго игрока.
Игрок А может выбрать любую чистую стратегию 
, 
, в ответ на которую игрок В может выбрать любую свою чистую стратегию 
, 
.
Если игра состоит только из личных ходов, то выбор пары стратегий 
однозначно определяет результат 
– выигрыш игрока А. При этом проигрыш игрока В составит 
(выигрыш игрока В равен). Если известны значения для каждой пары чистых стратегий, то можно составить матрицу выигрышей игрока А (проигрышей игрока В):
Определение 2. Прямоугольная матрица 
размерности 
, где 
(число строк) число чистых стратегий первого игрока, а 
– (число столбцов) число стратегий второго игрока, а в клетках указаны выигрыши игроков для каждой ситуации, называется платёжной матрицей игры (матрицей выигрышей, матрицей платежей) первого игрока.
|
|
|
Замечание 1. Платёжная матрица второго игрока: 
.
Замечание 2. Для наглядности матрицы выигрышей обоих игроков объединяют в матрицу, элементами которой являются упорядоченные пары, состоящие из выигрыша первого и проигрыша второго игрока при данной стратегии:
Такую матрицу называют биматрицей игры.
Пример 2.1 (парная конечная игра с нулевой суммой (антагонистическая парная игра)) [11]. Два игрока независимо друг от друга записывают любое целое число. Если выписанные числа имеют одинаковую чётность, то игрок А получает от игрока В 1 рубль, а если разную, то наоборот, игрок А платит игроку В 1 рубль. Требуется составить платёжную матрицу игры.
Решение. Игрок А имеет 2 стратегии:
Игрок В также имеет 2 стратегии:
Выбор игроками соответствующих стратегий и однозначно определяет исход игры: - выигрыш игрока А. Стратегиям и соответствует выигрыш игрока А, равный 1 рубль, а стратегиям и соответствует проигрыш игрока, равный 1 рубль (выигрыш, равный –1 рубль). Тогда платёжные матрицы будут иметь вид:
Пример 2.2 (парная конечная игра с ненулевой суммой) [1]. Две фирмы функционируют на рынке одновременно с одинаковым товарным объёмом Q. У обеих фирм по соображениям рентабельности есть следующие стратегии: либо вбросить на рынок полный объём товара Q, либо выбросить на рынок половину объёма 0,5Q. Если первая фирма выбрасывает на рынок полный объём товара, а вторая – половину объёма, то первая фирма получает 100% запланированной прибыли, а вторая – только 25%, и наоборот. Если обе фирмы выбрасывают на рынок по полному объёму прибыли, то получат по 15 % прибыли; если по половине объёма, то прибыль каждой из фирм составит по 50% от запланированной.
Решение. Примем долю прибыли (в %) от запланированной за значение выигрыша при каждой стратегии, тогда возможны следующие ситуации:
Запишем матрицы выигрышей обеих фирм и биматрицу игры:
|
|
|
Пример 2.3 (парная бесконечная игра) [1]. Две конкурирующие фирмы борются за рынки сбыта, других конкурентов в этом сегменте нет (дуополия). В этом случае каждый из игроков может назвать цену p, по которой он хочет продать определённое количество товара. При этом полагается, что потребители приобретут товар у фирмы, объявившей меньшую цену. В случае объявления одинаковой цены спрос 
распределяется между фирмами поровну.
Решение. Каждый из игроков обладает бесконечным числом стратегий. Функция выигрышей игроков характеризует величины дохода фирм в зависимости от объявленных цен. Так как доход фирмы 
, то функцию выигрышей игроков можно представить в виде:
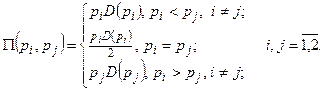
Определение 3. Игры двух игроков, функции выигрышей которых можно представить в виде матриц, называются матричными.
Замечание. Матричные игры являются наиболее разработанным направлением теории игр.
|
|
|
