 |
Игры без седловой точки в чистых стратегиях
|
|
|
|
Определение 12. Если платёжная матрица не имеет седлового элемента, то есть 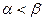 , то говорят, что игра не имеет решения в чистых стратегиях.
, то говорят, что игра не имеет решения в чистых стратегиях.
В этом случае для каждого игрока важно, чтобы соперник не угадал выбора его стратегии. В этом случае используются смешанные стратегии, при которых реализуется схема случайного выбора чистой стратегии.
Определение 13. Смешанной стратегией игрока А называется вероятностное распределение на множестве чистых стратегий этого игрока, задаваемого вектором 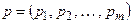 , элементы которого удовлетворяют условиям: 1)
, элементы которого удовлетворяют условиям: 1) 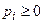 (
( ), 2)
), 2)  , где
, где 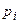 (
( ) – вероятности, с которыми игрок А выбирает свои чистые стратегии
) – вероятности, с которыми игрок А выбирает свои чистые стратегии  .
.
Определение 14. Смешанной стратегией игрока В называется вероятностное распределение на множестве чистых стратегий этого игрока, задаваемого вектором  , элементы которого удовлетворяют условиям:
, элементы которого удовлетворяют условиям:
1) 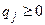 (
( ),
),
2) 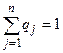 , где
, где  (
( ) – вероятности, с которыми игрок В выбирает свои чистые стратегии
) – вероятности, с которыми игрок В выбирает свои чистые стратегии 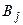 .
.
При использовании смешанных стратегий игра приобретает случайный характер. Выбор каждой пары чистых стратегий  является случайным событием и ввиду независимости случайных величин
является случайным событием и ввиду независимости случайных величин  и
и 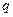 реализуется с вероятностью
реализуется с вероятностью 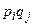 . Величина
. Величина  выигрыша игрока А (проигрыша игрока В) становится случайной величиной. Эта величина является функцией смешанных стратегий
выигрыша игрока А (проигрыша игрока В) становится случайной величиной. Эта величина является функцией смешанных стратегий  и
и 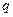 и определяется по формуле:
и определяется по формуле: 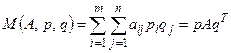 .
.
Определение 15. Функцию 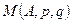 называют функцией выигрыша или платёжной функцией.
называют функцией выигрыша или платёжной функцией.
Замечание 1. Формально функция 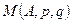 представляет собой математическое ожидание выигрыша игрока А в ситуации в смешанных стратегиях
представляет собой математическое ожидание выигрыша игрока А в ситуации в смешанных стратегиях  и
и 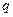 .
.
Замечание 2. На множестве смешанных стратегий игрок А, стремящийся достичь наибольшего из гарантированных выигрышей, выбирает вектор вероятностей  так, чтобы получить максимум минимальных значений ожидаемых выигрышей, то есть решает задачу максимина математического ожидания
так, чтобы получить максимум минимальных значений ожидаемых выигрышей, то есть решает задачу максимина математического ожидания  , то есть поиск вектора
, то есть поиск вектора  такого, что
такого, что
|
|
|
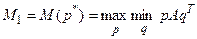 (6.1)
(6.1)
Соответственно, игрок В решает задачу минимакса математического ожидания 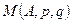 – поиск вектора
– поиск вектора 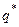 такого, что
такого, что  .
.
Определение 16. Смешанные стратегии 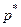 и
и 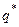 называются оптимальными, если они образуют седловую точку для платёжной функции
называются оптимальными, если они образуют седловую точку для платёжной функции 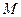 , то есть удовлетворяют неравенству
, то есть удовлетворяют неравенству 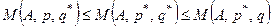 .
.
Определение 16’. Смешанные стратегии 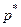 и
и 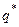 называются оптимальными, если имеет место равенство:
называются оптимальными, если имеет место равенство:
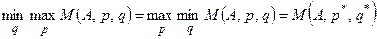 .
.
Замечание. Определения 16 и 16’ равносильны.
Определение 17. Величину 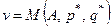 называют ценой игры.
называют ценой игры.
Определение 18. Набор  , состоящий из оптимальных смешанных стратегий
, состоящий из оптимальных смешанных стратегий 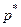 и
и 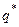 и цены игры
и цены игры  , называется решением матричной игры.
, называется решением матричной игры.
Определение 19. Стратегия 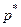 игрока А называется максиминной стратегией, стратегия
игрока А называется максиминной стратегией, стратегия 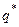 называется минимаксной стратегией.
называется минимаксной стратегией.
Возникают два ключевых вопроса:
1) какие матричные игры имеют решение в смешанных стратегиях?
2) как находить решение матричной игры, если он существует?
Теорема 2 (о минимаксе) (Дж. фон Нейман). Для матричной игры с любой платёжной матрицей 
1) величины 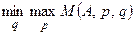 ,
,  существуют и равны между собой:
существуют и равны между собой:  .
.
2) существует хотя бы одна ситуация в смешанных стратегиях  , для которой выполняется соотношение:
, для которой выполняется соотношение:
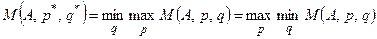 .
.
Теорема 3 (о свойствах оптимальных стратегий). Пусть 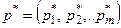 ;
; 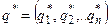 – оптимальные смешанные стратегии и
– оптимальные смешанные стратегии и 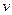 – цена игры. Тогда:
– цена игры. Тогда:
1) оптимальная смешанная стратегия 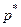 игрока А может быть составлена только из тех чистых стратегий
игрока А может быть составлена только из тех чистых стратегий  (
( ), для которых
), для которых  ;
;
2) оптимальная смешанная стратегия игрока В может быть составлена только из тех чистых стратегий  (
( ), для которых
), для которых  .
.
Следствие. Имеет место цепочка равенств:
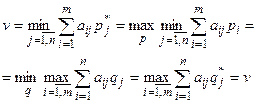
Пример 2.5 [1]. Найти решение игры, имеющей платёжную матрицу 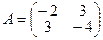 .
.
Решение. Найдём седловую точку данной матрицы:
Таким образом, седловая точка данной матрицы отсутствует. Задача не имеет решения в чистых стратегиях. Решение игры нужно искать в
|
|
|
Пусть оптимальные стратегии игроков определяются, соответственно векторами вероятностей 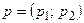 ,
,  , для которых
, для которых 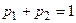 ,
, 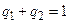 – условия нормировки. Функция выигрыша будет иметь вид:
– условия нормировки. Функция выигрыша будет иметь вид:

 .
.
Так как, согласно (6.1), требуется найти максимум функции выигрыша, то должно быть  и, следовательно, должно выполняться равенство:
и, следовательно, должно выполняться равенство: 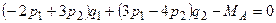 . Система уравнений для определения оптимальных стратегий
. Система уравнений для определения оптимальных стратегий 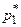 и
и  имеет вид:
имеет вид:
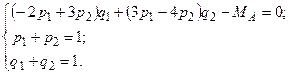
В ней содержится 3 уравнения и 5 неизвестных.
Для отыскания 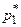 и
и  воспользуемся следующим приёмом. Так как
воспользуемся следующим приёмом. Так как  и
и  , то имеем право записать:
, то имеем право записать: 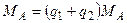 . Подставим полученное соотношение в первое уравнение системы, получим:
. Подставим полученное соотношение в первое уравнение системы, получим:
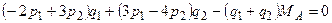 ; или
; или
 .
.
Так как по теореме 3 значения 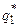 и
и  должны быть отличны от нуля (как оптимальные), то последнее равенство выполняется при произвольных положительных
должны быть отличны от нуля (как оптимальные), то последнее равенство выполняется при произвольных положительных 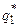 и
и  только в том случае, когда
только в том случае, когда
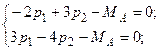 или
или  .
.
Так как  , то
, то 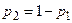 , следовательно,
, следовательно,
 .
.
Решая полученное уравнение, получаем 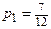 , тогда
, тогда 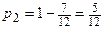 . Таким образом, вероятности оптимальных стратегий первого игрока
. Таким образом, вероятности оптимальных стратегий первого игрока 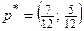 .
.
Аналогично для отыскания  и
и 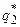 из соотношений
из соотношений  и
и  имеем право записать:
имеем право записать: 
Подставим полученное соотношение в первое уравнение системы, получим:
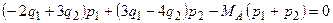 или
или
 .
.
Так как по теореме 3 значения 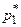 и
и  должны быть отличны от нуля (как оптимальные), то последнее равенство выполняется при произвольных положительных
должны быть отличны от нуля (как оптимальные), то последнее равенство выполняется при произвольных положительных 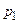 и
и  только в том случае, когда
только в том случае, когда
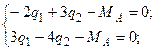 или
или 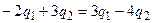 .
.
Так как  , то
, то  , и, следовательно, последнее уравнение примет вид:
, и, следовательно, последнее уравнение примет вид:  . Решая его, получаем
. Решая его, получаем 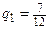 ,
, 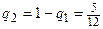 . Таким образом, вероятности оптимальных стратегий второго игрока определяются вектором
. Таким образом, вероятности оптимальных стратегий второго игрока определяются вектором 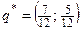 .
.
Подставим найденные оптимальные вероятности смешанных стратегий в функцию выигрыша, найдём цену игры:
 .
.
Ответ. 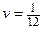 ;
; 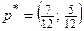 ;
; 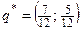 .
.
|
|
|


