 |
Игры с седловой точкой в чистых стратегиях
|
|
|
|
Определение 4. Парная игра, в которой сумма выигрышей игроков равна нулю (выигрыш первого игрока равен проигрышу второго игрока) называется парной игрой с нулевой суммой или антагонистической игрой.
Замечание. Всякую парную игру с нулевой суммой всегда можно полностью задать платёжной матрицей одного из игроков. Как правило, задают платёжную матрицу первого игрока. Предполагается, что все игроки одинаково разумны. Задача каждого игрокасостоит в том, что каждый игрок стремится обеспечить себе максимально возможный выигрыш при любых действиях другого игрока.
Пусть платёжная матрица первого игрока в игре двух игроков, имеющих соответственно  и
и  стратегий, имеет вид
стратегий, имеет вид  . Тогда матрица выигрышей второго игрока
. Тогда матрица выигрышей второго игрока  .
.
Построим оптимальные стратегии игроков в антагонистической игре.
Оптимальная стратегия первого игрока. Первый игрок желает получить максимальный собственный выигрыш. При этом он предполагает, что в любом случае второй игрок выберет стратегию, минимизирующую выигрыш первого игрока. Задача первого игрока – получить некоторый гарантированный выигрыш.
Обозначим минимальное значение выигрыша первого игрока при каждой его стратегии (в каждой строке матрицы  ):
):  ,
,  . Зная минимальные выигрыши
. Зная минимальные выигрыши 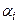 при различных стратегиях
при различных стратегиях  второго игрока, первый игрок выберет ту стратегию, при которой
второго игрока, первый игрок выберет ту стратегию, при которой 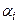 максимально. Обозначим это значение
максимально. Обозначим это значение 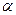 . Тогда
. Тогда  .
.
Определение 5. Величина 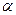 – гарантированный максимальный выигрыш, который может обеспечить себе первый игрок, – называется нижней ценой игры или максимином.
– гарантированный максимальный выигрыш, который может обеспечить себе первый игрок, – называется нижней ценой игры или максимином.
Таким образом, формально оптимальная стратегия первого игрока состоит в выборе строки и в ней элемента матрицы  :
: 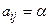 . Эта стратегия называется максиминной со стороны первого игрока. Если первый игрок будет придерживаться максиминной стратегии, то его выигрыш в любом случае будет не меньше максиминного значения:
. Эта стратегия называется максиминной со стороны первого игрока. Если первый игрок будет придерживаться максиминной стратегии, то его выигрыш в любом случае будет не меньше максиминного значения:
|
|
|
Оптимальная стратегия второго игрока. Второй игрок желает минимизировать собственный проигрыш. При этом он предполагает, что в любом случае первый игрок выберет стратегию, максимизирующую собственный выигрыш. Задача второго игрока – проиграть не более некоторой гарантированной суммы.
Обозначим максимальное значение выигрыша первого игрока при каждой стратегии второго игрока (в каждом столбце матрицы  ):
): 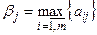 ,
,  . Зная максимальные выигрыши первого игрока
. Зная максимальные выигрыши первого игрока  при различных стратегиях второго игрока
при различных стратегиях второго игрока  , второй игрок выберет ту стратегию, при которой
, второй игрок выберет ту стратегию, при которой  минимально. Обозначим это значение
минимально. Обозначим это значение  . Тогда
. Тогда  .
.
Определение 6. Величина  – минимальный проигрыш, который может обеспечить себе второй игрок, – называется верхней ценой игры или минимаксом.
– минимальный проигрыш, который может обеспечить себе второй игрок, – называется верхней ценой игры или минимаксом.
Таким образом, формально оптимальная стратегия второго игрока состоит в выборе столбца и в ней элемента матрицы  :
:  . Эта стратегия называется минимаксной со стороны второго игрока. Если второй игрок будет придерживаться минимаксной стратегии, то он в любом случае проиграет не больше минимаксного значения:
. Эта стратегия называется минимаксной со стороны второго игрока. Если второй игрок будет придерживаться минимаксной стратегии, то он в любом случае проиграет не больше минимаксного значения:
Теорема 1. Для произвольной прямоугольной матрицы всегда выполняется неравенство  или
или 
Определение 7. Если верхняя цена игры равна нижней, то есть  , то говорят, что игра имеет седловую точку (решается) в чистых стратегиях.
, то говорят, что игра имеет седловую точку (решается) в чистых стратегиях.
Определение 8. Значение 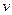 называется ценой игры (чистой ценой игры).
называется ценой игры (чистой ценой игры).
Определение 9. Элемент матрицы 
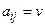 называется седловым элементом матрицы
называется седловым элементом матрицы  .
.
Замечание. Седловой элемент матрицы  одновременно является минимальным в своей строке и максимальным в своём столбце, то есть
одновременно является минимальным в своей строке и максимальным в своём столбце, то есть 
Определение 10. Пару чистых стратегий  и
и  , соответствующих
, соответствующих 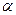 и
и  , называют седловой точкой игры.
, называют седловой точкой игры.
Замечание. Стратегии  и
и  , образующие седловую точку, являются оптимальными. Существование седловой точки платёжной матрицы соответствует наличию состояния равновесия в данной матричной игре.
, образующие седловую точку, являются оптимальными. Существование седловой точки платёжной матрицы соответствует наличию состояния равновесия в данной матричной игре.
|
|
|
Определение 11. Тройка  называется решением игры.
называется решением игры.
Пример 2.4 [2]. В игре участвуют два игрока. Каждый из них может записать независимо от другого цифры 1, 2 и 3. если разность между цифрами, записанными игроками, положительна, то первый игрок выигрывает количество очков, равное разности между цифрами. Если разность отрицательна, то выигрывает второй игрок. Если разность нулевая, то игра заканчивается вничью. Составить платёжную матрицу и найти цену игры.
Решение. У игрока А есть 3 стратегии:
У игрока В также есть три стратегии:
Данная игра является парной игрой с противоположными интересами (антагонистической), следовательно, для её формального описания достаточно задать платёжную матрицу первого игрока.
Вычислим возможные выигрыши первого игрока:
Тогда платёжная матрица первого игрока примет вид:
Найдём оптимальную стратегию первого игрока. Для этого найдём минимальный выигрыш при каждой его стратегии (минимальный элемент в каждой строке):
Найдём нижнюю цену игры (выберем из минимальных элементов наибольший):
Таким образом, оптимальная стратегия первого игрока:
Найдём оптимальную стратегию второго игрока. Для этого найдём максимальный выигрыш первого игрока при каждой стратегии второго игрока (максимальный элемент в каждом столбце):
Найдём верхнюю цену игры (выберем из максимальных элементов наименьший):
Таким образом, оптимальная стратегия второго игрока:
Отклонение первого игрока от оптимальной стратегии уменьшает его выигрыш. Отклонение второго игрока от оптимальной стратегии увеличивает его проигрыш.
Ответ.
|
|
|


