Моделирование игровых ситуаций

2. Игра Моро. Каждый из игроков А и В записывает одно из чисел 1, 4, 6 или 9. Затем они одновременно показывают написанное. Если оба числа оказались одинаковой четности, то игрок А выигрывает столько очков, какова сумма этих чисел. Если записанные числа разной четности, то выигрывает игрок В. Составить платежную матрицу, найти верхнюю и нижнюю цены игры, максиминную и минимаксную стратегии игроков.

3. Два игрока А и В, не глядя друг на друга, кладут на стол по картонному кружку красного, зеленого или синего цвета, сравнивают цвета кружков и расплачиваются друг с другом, как показано в матрице игры (строки соответствуют стратегиям игрока А). Выписать все возможные ситуации выигрышей и проигрышей игрока А. Определить оптимальные стратегии игроков.

4. «Веришь – не веришь». Имеются 2 карты: туз и двойка. Игрок А наугад вынимает одну из них, игрок В не видит, какую из карт вынул игрок А. Если А вынул туза, он заявляет «у меня туз» и требует у противника 1 рубль. Если А вынул двойку, то он может либо сказать «у меня туз» и потребовать у противника 1 рубль, либо признаться, что у него двойка и уплатить противнику 1 рубль. Противник, если ему добровольно платят рубль, может только принять его. Если же у него потребуют 1 рубль, то он может либо поверить игроку А, что у него туз и отдать ему 1 рубль, или потребовать проверки с тем, чтобы убедиться, что утверждение игрока А верно. Если в результате проверки окажется, что игрока А действительно туз, то В должен уплатить А 2 рубля. Если же окажется, что А обманывает В, то А платит игроку В 2 рубля. Составит модель игры и найти оптимальные стратегии игроков.

5. Игроки А и В записывают цифры 1 и 2. Игра состоит в том, что кроме цифры 1 или 2 каждый игрок записывает ещё и ту цифру, которую, по его мнению, записал партнёр. Если оба игрока угадали или оба ошиблись, то партия заканчивается вничью. Если же угадал один, то он получает столько очков, какова сумма записанных им цифр. Составить платёжную матрицу и решение игры.

6. Игрок А может записать одну из цифр:2, 4 или 7. Игрок В может записать 1, 3, 4 или 8. Если обе цифры окажутся одинаковой чётности, то игрок А получает столько очков, какова сумма записанных цифр. Если разной чётности, то очки присуждаются игроку В. Составить платёжную матрицу и решение игры.

7. Участники парной игры независимо друг от друга могут записать одну из цифр: 3, 5 или 8. Если разность между цифрами, записанными игроками А и В окажется положительной, то игрок А выигрывает столько очков, какова получившаяся разность. Если разность будет отрицательной, то соответствующее количество очков выигрывает игрок В. Если разность окажется равной нулю, то выигрыш игроков будет равен нулю. Составить платёжную матрицу и найти решение игры.

8. Камень, ножницы, бумага». Игроки одновременно называют один из предметов, причём «камень» побеждает «ножницы», «ножницы» побеждают «бумагу», «бумага» побеждает «камень». Игрок, который назовёт выигрывающий предмет, выигрывает у противника очко. Если оба выберут одинаковые предметы, то игра заканчивается вничью. Составить платёжную матрицу и найти решение игры.

9. «Проблема полковника Блотто». Две воюющие армии ведут борьбу за 2 пункта. Первая армия по командованием полковника Блотто состоит из 4-х полков. Вторая под командованием капитана Киже – из 3-х полков. Армия, которая посылает больше полков на тот или иной населённый пункт, занимает его и уничтожает все направленные в этот пункт силы противника, получая по 1 баллу как за занятый пункт, так и за каждый уничтоженный пункт противника. Требуется распределить силы так, чтобы получить максимальное количество баллов.

10. Два игрока А и В, не глядя друг на друга, кладут на стол по монете гербом вверх или вверх цифрой, по своему усмотрению. Если игроки выбрали одинаковые стороны (у обоих герб или у обоих цифра), то игрок А забирает обе монеты; иначе их забирает игрок В. Составить платёжную матрицу, найти верхнюю и нижнюю цены игры, максиминную и минимаксную стратегии игроков. Если возможно, найдите оптимальные чистые стратегии игроков и чистую цену игры.

11. Игроки А и В одновременно и независимо друг от друга записывают каждый одно из 3-х чисел: 1, 2 или 3. Если сумма записанных чисел чётная, то игрок В платит игроку А эту сумму в рублях; ели она нечётная, то, наоборот, А платит В эту сумму. Составить платёжную матрицу, найти верхнюю и нижнюю цены игры, максиминную и минимаксную стратегии игроков. Если возможно, найдите оптимальные чистые стратегии игроков и чистую цену игры.

12. Воздушный бой. В распоряжении воюющей стороны А имеются 3 вида вооружения , , ; у противника В – 3 вида самолётов: , , 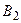. Задача стороны А – поразить самолёт; задача противника – сохранить его непоражённым. При применении вооружения самолёты , , 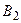поражаются соответственно с вероятностями 0,9; 0,4 и 0,2; при вооружении – с вероятностями 0,3; 0,6 и 0,8; при вооружении – с вероятностями 0,5; 0,7 и 0,2. Составить платёжную матрицу стороны А, найти верхнюю и нижнюю цены игры, максиминную и минимаксную стратегии игроков. Если возможно, найдите оптимальные чистые стратегии игроков и чистую цену игры.

13. Дилемма узников. Два узниканаходятся в предварительном заключении по подозрению в совершении преступления. При отсутствии прямых улик возможность их осуждения зависит от того, будут они молчать или заговорят. Если оба будут молчать, то наказанием будет лишь срок предварительного заключения (величина потерь (-1) для каждого). Если оба сознаются, то получат срок, учитывающий признание как смягчающее обстоятельство (потери кждого из узников составят (-6)). Если же заговорит один из узников, а другой будет молчать, то заговоривший будет выпущен на свободу (потери (0)), а сохраняющий молчание получит максимальное наказание (потери (-10)). Составить платёжные матрицы для каждого из игроков, найти верхнюю и нижнюю цены игры, максиминную и минимаксную стратегии игроков. Если возможно, найдите оптимальные чистые стратегии игроков и чистую цену игры.

14. Семейный спор. Муж и жена собираются провести вместе субботний вечер. Жена хочет сходить в театр, а муж – на футбол. Если оба идут в театр, то выигрыш жены вдвое больше выигрыша мужа. Если оба идут на футбол, то выигрыш мужа вдвое больше выигрыша жены. Если же супругам пришлось проводить вечер по одному, то выигрыш обоих равен нулю. Составить платёжную матрицу стороны А, найти верхнюю и нижнюю цены игры, максиминную и минимаксную стратегии игроков. Если возможно, найдите оптимальные чистые стратегии игроков и чистую цену игры.

15. Студент-преподаватель. Студент (игрок А) собирается сдавать зачёт, который принимает преподаватель В. Если студент подготовился и получил зачёт, то его выигрыш на 1 больше выигрыша в ситуации, когда не готовился и получил зачёт, на 2 единицы больше, чем когда не готовился и не получил (в этой ситуации выигрыш равен 0), и на 3 единицы больше, чем когда готовился и не получил. Выигрыш преподавателя равен 1, если зачет получил подготовленный студент, что на 2 больше выигрыша в ситуации, когда неподготовленный студент не получил зачёт, на 3 больше выигрыша в ситуации, когда неподготовленному студенту удалось получить зачёт, и на 4 больше выигрыша в ситуации, когда подготовленный студент не получил зачёт. Составить платёжные матрицы игроков.

Игры с природой

16. Предприятие, торгующее мороженым, провело маркетинговые исследования и выяснило, что в хорошую погоду продаётся объём продукции с прибылью . В плохую погоду продаётся объём продукции с прибылью, составляющей 65% от прибыли . Если предприятие завезло продукцию в объёме , а погода была хорошей, то оно терпит убыток 35% от прибыли . Если же предприятие завезло продукцию в объёме , а погода была плохой, то оно терпит убыток 45% от прибыли . Составить платёжную матрицу стороны А (предприятия), найти верхнюю и нижнюю цены игры, максиминную и минимаксную стратегии игроков. Если возможно, найдите оптимальные чистые стратегии игроков и чистую цену игры.

17. Фермер может засеять угодья двумя культурами: и . Урожайность (и соответственно прибыль) зависят от типа лета – жаркого, 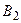– умеренного, – холодного. Культура обеспечивает прибыль: при погоде 8 млн. руб., при погоде 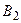5 млн. руб., при погоде 3 млн. руб. Культура обеспечивает прибыль: при погоде 2 млн. руб., при погоде 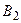3 млн. руб., при погоде 6 млн. руб. Составить платёжную матрицу стороны А (фермера), найти верхнюю и нижнюю цены игры, максиминную и минимаксную стратегии игроков. Если возможно, найдите оптимальные чистые стратегии игроков и чистую цену игры.

18. Розничное торговое предприятие разработало несколько вариантов плана продаж товара на предстоящей ярмарке с учетом конъюнктуры рынка и спроса покупателей. Получающиеся от их возможных сочетаний показатели прибыли указаны в таблице. Определить:

а) оптимальный план продажи товаров и цену игры,

б) какой стратегии следует придерживаться торговому предприятию, если наиболее вероятной является ситуация: , , ?

План продажи	Величина прибыли в зависимости от спроса, млн. руб.

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Основная литература

1. Красс М.С., Чупрынов Б.П. Математика для экономистов. СПб.: Питер, 2005.

2. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. М.: Дело, 2002.

3. Данко П.Е., Кожевникова С.Я., Попов А.Г. Высшая математика в упражнениях и задачах. В 2-х частях. Учеб. пособие для втузов. М.: Высшая школа, 2000.

4. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. – М.: МГУ им М.В. Ломоносова, Изд-во ДИС, 1998.

Дополнительная литература

5. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. М.: Финансы и статистика, 2002.

6. Сборник задач и упражнений по высшей математике: Мат. программирование: Учеб. пособие / А.В. Кузнецов, В.А. Сакович, Н.И. Холод и др.; Под ред. А.В. Кузнецова, Р.А. Рутковского. Минск: Выш. шк., 2002.

7. Колемаев В.А. Математическая экономика. М.: ЮНИТИ, 1998.

8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под. ред. В.В. Федосеева. – М.: ЮНИТИ, 2002.

9. Красс М.С. Математика для экономических специальностей: Учебник. М.: Дело, 2002.

10. Кундышева Е.С. Математическое моделирование в экономике: Учебное пособие. М.: Издательско-торговая корпорация Дашков и К^о, 2004.

11. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие. М.: Дело, 2002.

12. Пинегина М.В., Математические методы и модели в экономике. Учебное пособие. М.: Экзамен, 2002.

13. Лискина Е.Ю. Математика: практикум. Ч. 1. Рязань: Изд-во РГПУ им. С.А. Есенина, 2004.

14. Математические методы исследования экономики. Гипертекст. / Составитель Е.С. Поволоцкая. М.: Современный гуманитарный университет, 1997

15. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М., 1976.

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: