 |
Поиск оптимальной смешанной стратегии первого игрока
|
|
|
|
Согласно теореме 3,
 .
.
Тогда нахождение цены игры 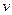 и оптимального вектора
и оптимального вектора  для игрока А равносильно решению уравнения
для игрока А равносильно решению уравнения  .
.
Рассмотрим функцию  . Это функция одной переменной
. Это функция одной переменной  с набором
с набором 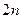 параметров
параметров  . Следовательно, решение уравнения
. Следовательно, решение уравнения  равносильно нахождению максимума функции
равносильно нахождению максимума функции  на отрезке
на отрезке  .
.
Формально для нахождения максимума функции  на отрезке
на отрезке  требуется
требуется
1) построить график функции  на отрезке
на отрезке  ;
;
2) найти координаты наивысшей точки построенного графика.
Для построения графика функции 
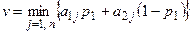 требуется построить всевозможные прямые
требуется построить всевозможные прямые  ,
,  , а затем найти ломаную, состоящую из отрезков этих прямых, такую, что она расположена не выше каждой прямой. Такую ломаную называют нижней огибающей прямых
, а затем найти ломаную, состоящую из отрезков этих прямых, такую, что она расположена не выше каждой прямой. Такую ломаную называют нижней огибающей прямых  ,
,  . Нижняя огибающая и будет являться графиком функции
. Нижняя огибающая и будет являться графиком функции  .
.
Замечание. С точки зрения теории игр построение нижней огибающей прямых  ,
,  равносильно следующим рассуждениям. Предположим, что игрок А выбрал смешанную стратегию
равносильно следующим рассуждениям. Предположим, что игрок А выбрал смешанную стратегию  , а игрок В –
, а игрок В –  -ю чистую стратегию
-ю чистую стратегию  ,
,  . Тогда средний выигрыш игрока А в ситуации
. Тогда средний выигрыш игрока А в ситуации  оказывается равным
оказывается равным  . Это уравнение прямой на плоскости
. Это уравнение прямой на плоскости  . Таким образом, каждой чистой стратегии игрока В на плоскости
. Таким образом, каждой чистой стратегии игрока В на плоскости  соответствует своя прямая. Все чистые стратегии игрока В описываются системой прямых
соответствует своя прямая. Все чистые стратегии игрока В описываются системой прямых  ,
,  . Так как
. Так как  – минимальный средний выигрыш по всем чистым стратегиям игрока В, то нижняя огибающая семейства прямых
– минимальный средний выигрыш по всем чистым стратегиям игрока В, то нижняя огибающая семейства прямых  ,
,  будет являться таким минимальным средним выигрышем. Цена игры
будет являться таким минимальным средним выигрышем. Цена игры  (максимальный из всех минимальных средних выигрышей) будет являться наивысшей точкой нижней огибающей.
(максимальный из всех минимальных средних выигрышей) будет являться наивысшей точкой нижней огибающей.
Для нахождения координат наивысшей точки нижней огибающей нужно выделить прямые, проходящие через эту точку, и решить систему уравнений, составленную из уравнений этих прямых.
|
|
|
Практическое замечание. Уравнения семейства прямых  ,
,  составляются по столбцам платёжной матрицы
составляются по столбцам платёжной матрицы  .
.
Поиск оптимальной смешанной стратегии второго игрока. В зависимости от формы нижней огибающей может представиться несколько случаев.
Случай 1. Нижняя огибающая имеет ровно одну наивысшую точку  .
.
1) Если 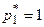 (игрок А выбрал чистую стратегию
(игрок А выбрал чистую стратегию  ), то игроку В выгодно применять чистую стратегию, соответствующую прямой, проходящей через точку
), то игроку В выгодно применять чистую стратегию, соответствующую прямой, проходящей через точку  и имеющей наименьший положительный наклон.
и имеющей наименьший положительный наклон.
2) Если 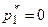 (игрок А выбрал чистую стратегию
(игрок А выбрал чистую стратегию  ), то игроку В выгодно применять чистую стратегию выгодно применять чистую стратегию, соответствующую прямой, проходящей через точку
), то игроку В выгодно применять чистую стратегию выгодно применять чистую стратегию, соответствующую прямой, проходящей через точку  и имеющей наибольший отрицательный наклон.
и имеющей наибольший отрицательный наклон.
3) Если  , то в наивысшей точке нижней огибающей пересекаются по меньшей мере две прямые, одна из которых (например,
, то в наивысшей точке нижней огибающей пересекаются по меньшей мере две прямые, одна из которых (например, 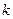 -я) имеет положительный наклон, а другая (например,
-я) имеет положительный наклон, а другая (например, 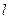 -я) – отрицательный. Это означает, что игроку В наиболее выгодно использовать смешанную стратегию, состоящую из стратегий
-я) – отрицательный. Это означает, что игроку В наиболее выгодно использовать смешанную стратегию, состоящую из стратегий 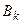 и
и  с вероятностями
с вероятностями  и
и 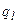 соответственно. Оптимальную смешанную стратегия игрока В можно найти как решение системы уравнений
соответственно. Оптимальную смешанную стратегия игрока В можно найти как решение системы уравнений

Геометрически решение этой системы уравнений соответствует нахождению нижней точки верхней огибающей семейства прямых 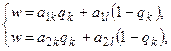 , где
, где  .
.
Замечание. Верхней огибающей семейства прямых называют ломаную, состоящую из отрезков прямых этого семейства, расположенную не ниже каждой прямой.
С точки зрения теории игр и в соответствии с теоремой 3 нижняя точка верхней огибающей системы прямых 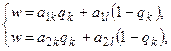 является минимаксом для второго игрока:
является минимаксом для второго игрока:

 .
.
Практическое замечание. Уравнения прямых
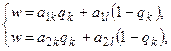
составляются по строкам матрицы 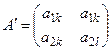 , полученной из матрицы
, полученной из матрицы  исключением невыгодных для второго игрока стратегий.
исключением невыгодных для второго игрока стратегий.
Случай 2. Нижняя огибающая имеет горизонтальный участок, соответствующий чистой стратегии 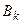 игрока В, наиболее выгодной для него.
игрока В, наиболее выгодной для него.
Пример 2.7 [2]. Найти решение  -игры, заданной платёжной матрицей
-игры, заданной платёжной матрицей
|
|
|
 .
.
Решение. 1) Найдём верхнюю и нижнюю цены игры:
 ,
, 
 . Так как
. Так как  , то седловой точки в чистых стратегиях нет.
, то седловой точки в чистых стратегиях нет.
Обозначим:  – вероятность применения первым игроком стратегии
– вероятность применения первым игроком стратегии  ;
;
 – вероятность применения первым игроком стратегии
– вероятность применения первым игроком стратегии  ;
;
 – вероятность применения вторым игроком стратегии
– вероятность применения вторым игроком стратегии  ;
;
 – вероятность применения вторым игроком стратегии
– вероятность применения вторым игроком стратегии 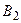 ;
;
 – вероятность применения вторым игроком стратегии
– вероятность применения вторым игроком стратегии  ;
;
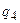 – вероятность применения вторым игроком стратегии
– вероятность применения вторым игроком стратегии  ;
;
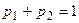 ,
,  .
.
2) Найдём оптимальную смешанную стратегию первого игрока.
А) Составим таблицу ожидаемых средних выигрышей первого игрока в зависимости от стратегий второго игрока (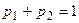 ) (уравнения составляют по столбцам платёжной матрицы).
) (уравнения составляют по столбцам платёжной матрицы).
Таблица 7.1.
| Стратегии второго игрока | Ожидаемый выигрыш первого игрока | Уравнение прямой |

| 
| 
|
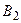
| 
| 
|

| 
| 
|

| 
| 
|
Б) Построим полученные прямые при  (см. рис. 7.1).
(см. рис. 7.1).
Напоминание. Прямую можно построить по двум точкам. В качестве точек удобно брать концы отрезка  и значения
и значения  на концах отрезка. Из рис. 7.1 видно, что нижняя огибающая данного семейства прямых образована прямыми
на концах отрезка. Из рис. 7.1 видно, что нижняя огибающая данного семейства прямых образована прямыми  и
и  .
.
В) Найдём точку пересечения прямых  и
и  как решение системы уравнений
как решение системы уравнений  Тогда
Тогда  , и, выражая
, и, выражая  , получим
, получим  . Следовательно,
. Следовательно,  .
.
Таким образом, оптимальная смешанная стратегия первого игрока заключается в равновероятном применении стратегий  и
и  :
:  .
.
Г) Найдём цену игры. Для этого подставим вектор  любое из уравнений
любое из уравнений  и
и  , например, в
, например, в  . Тогда цена игры
. Тогда цена игры  (максимальный гарантированный выигрыш первого игрока).
(максимальный гарантированный выигрыш первого игрока).
3) Найдём оптимальную смешанную стратегию второго игрока.
А) Найдём выгодные стратегии второго игрока. Через точку максимина первого игрока проходят три прямые:  ,
,  и
и  , соответствующими стратегиям
, соответствующими стратегиям 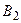 ,
,  и
и  второго игрока (см. табл. 7.1). Следовательно, стратегии
второго игрока (см. табл. 7.1). Следовательно, стратегии 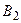 ,
,  и
и  будут более выгодными для второго игрока по сравнению со стратегией
будут более выгодными для второго игрока по сравнению со стратегией  .
.
 Для того, чтобы найти оптимальную смешанную стратегию второго игрока графическим методом, нужно выбрать из стратегий
Для того, чтобы найти оптимальную смешанную стратегию второго игрока графическим методом, нужно выбрать из стратегий 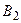 ,
,  и
и  две наиболее выгодных. В этом случае более выгодными для второго игрока являются стратегии
две наиболее выгодных. В этом случае более выгодными для второго игрока являются стратегии 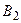 и
и  , так как именно они определяют значение минимакса
, так как именно они определяют значение минимакса 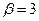 (см. п. 1) поиск нижней цены игры).
(см. п. 1) поиск нижней цены игры).
 Б) Найдём упрощённую платёжную матрицу. Исключим из платёжной матрицы невыгодные стратегии
Б) Найдём упрощённую платёжную матрицу. Исключим из платёжной матрицы невыгодные стратегии  и
и  (соответственно, вычеркнем первый и четвёртый столбцы, соответствующие вероятности
(соответственно, вычеркнем первый и четвёртый столбцы, соответствующие вероятности  ). Получим упрощённую платёжную матрицу
). Получим упрощённую платёжную матрицу  .
.
|
|
|
В) Составим таблицу ожидаемых средних проигрышей второго игрока ( ) (уравнения составляют по строкам упрощённой платёжной матрицы):
) (уравнения составляют по строкам упрощённой платёжной матрицы):
| Стратегии первого игрока | Ожидаемый проигрыш второго игрока | Уравнение прямой |

| 
| 
|

| 
| 
|
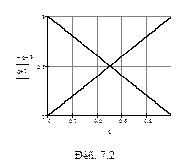
Г) Построим прямые  и
и  (см. рис. 7.2).
(см. рис. 7.2).
Д) Найдём точку пересечения прямых  и
и  из уравнения
из уравнения  . Тогда
. Тогда  ,
,  .
.
Таким образом, оптимальная смешанная стратегия второго игрока имеет вид  и заключается в равновероятном применении чистых стратегий
и заключается в равновероятном применении чистых стратегий  и
и  .
.
Ответ: смешанные стратегии первого игрока  , смешанные стратегии второго игрока
, смешанные стратегии второго игрока  , цена игры
, цена игры  .
.
2.3.2.  -игры
-игры
Определение 24. Матричную игру, в которой число стратегий первого игрока равно  , а число стратегий второго игрока равно двум, называется
, а число стратегий второго игрока равно двум, называется  - игрой.
- игрой.
Платёжная матрица  -игры имеет вид
-игры имеет вид  .
.
Графическое решение  -игры во многом аналогично графическому решению
-игры во многом аналогично графическому решению  -игры, но проходит в другой последовательности.
-игры, но проходит в другой последовательности.
1) Находят оптимальные стратегии второго игрока. Для этого:
А) выписывают уравнения для ожидаемых средних проигрышей второго игрока (уравнения составляют для переменных  и
и  по строкам платёжной матрицы при условии
по строкам платёжной матрицы при условии  );
);
Б) строят семейство прямых, соответствующих уравнениям средних проигрышей второго игрока;
В) строят верхнюю огибающую построенного семейства;
Г) выделяют низшую точку верхней огибающей, прямые, проходящие через эту точку, и находят координаты низшей точки верхней огибающей (минимакс второго игрока);
Д) находят оптимальную смешанную стратегию второго игрока из соотношения  ; находят цену игры, подставляя оптимальную смешанную стратегию второго игрока в уравнение любой прямой, проходящей через минимакс.
; находят цену игры, подставляя оптимальную смешанную стратегию второго игрока в уравнение любой прямой, проходящей через минимакс.
2) Находят оптимальную смешанную стратегию первого игрока. Для этого:
А) исходя из уравнений прямых, проходящих через минимакс второго игрока, и соответствующих им стратегий, выделяют две наиболее выгодные стратегии первого игрока;
|
|
|
Б) для выделенных стратегий составляют упрощённую платёжную матрицу;
В) по упрощённой матрице составляют уравнения ожидаемых средних выигрышей первого игрока; строят прямые, соответствующие уравнениям ожидаемых средних выигрышей первого игрока, и их нижнюю огибающую;
Г) находят оптимальную смешанную стратегию первого игрока как точку пересечения прямых ожидаемых средних выигрышей первого игрока (верхнюю точку нижней огибающей).
Определение 25. Матричную игру, заданную платёжной матрицей размерности  называют
называют  -игрой.
-игрой.
Замечание. Если матричную  игру можно свести к игре
игру можно свести к игре  или
или  , то её всегда можно решить графическим методом.
, то её всегда можно решить графическим методом.
2.4. Сведение матричной игры
к задаче линейного программирования
Если матричную  -игру нельзя свести к игре
-игру нельзя свести к игре  или
или  , то её сводят к паре двойственных задач линейного программирования.
, то её сводят к паре двойственных задач линейного программирования.
Пусть 1) платёжная матрица первого игрока в игре двух игроков, имеющих соответственно  и
и  стратегий, имеет вид
стратегий, имеет вид  ;
;
2) игра не имеет седловой точки в чистых стратегиях;
3) упрощением платёжной матрицы  -игру нельзя свести к игре
-игру нельзя свести к игре  или
или  .
.
Построим двойственную пару задач линейного программирования для  -игры.
-игры.
Задача линейного программирования для первого игрока. Управляющими переменными ЗЛП для первого игрока будут являться компоненты вектора  , удовлетворяющие условиям:
, удовлетворяющие условиям:  и
и  (
( ). Целевая функция для пары задач – это цена игры
). Целевая функция для пары задач – это цена игры  . Для первого игрока она примет вид
. Для первого игрока она примет вид  .
.
Для первого игрока цель игры заключается в максимизации выигрыша, т.е в нахождении такой смешанной стратегии  , которая максимизировала бы цену игры первого игрока при любых действиях второго игрока. Поэтому направление оптимизации целевой функции
, которая максимизировала бы цену игры первого игрока при любых действиях второго игрока. Поэтому направление оптимизации целевой функции 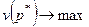 . При этом, согласно теореме 3, применение первым игроком оптимальной стратегии даёт выигрыш, не меньший цены игры, то есть
. При этом, согласно теореме 3, применение первым игроком оптимальной стратегии даёт выигрыш, не меньший цены игры, то есть  (
( ). Объединяя полученные соотношения в систему, получаем ЗЛП первого игрока:
). Объединяя полученные соотношения в систему, получаем ЗЛП первого игрока:
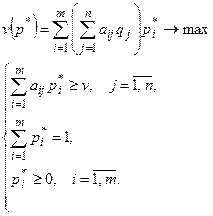
Коэффициентами целевой функции ЗЛП первого игрока являются величины  , которые меняются в зависимости от поведения второго игрока (меняется вектор
, которые меняются в зависимости от поведения второго игрока (меняется вектор  ).
).
Исключим величины  из ЗЛП первого игрока. Для этого, предполагая, что
из ЗЛП первого игрока. Для этого, предполагая, что  , разделим все соотношения системы ограничений на
, разделим все соотношения системы ограничений на 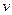 :
:
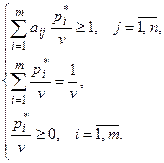
Выполним замену переменных:  (
( ). Так как
). Так как 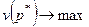 , то
, то  . Обозначим
. Обозначим  тогда ЗЛП первого игрока примет окончательный вид:
тогда ЗЛП первого игрока примет окончательный вид:
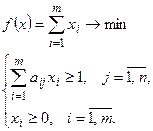
Аналогично строится задача линейного программирования для второго игрока.
Задача линейного программирования для второго игрока. Управляющими переменными ЗЛП для первого игрока будут являться компоненты вектора  , удовлетворяющие условиям:
, удовлетворяющие условиям: 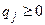 и
и  (
( ). Целевая функция для второго игрока примет вид
). Целевая функция для второго игрока примет вид 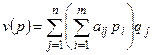 .
.
Для первого игрока цель игры заключается в минимизации проигрыша, т.е в нахождении такой смешанной стратегии  , которая минимизировала бы цену игры первого игрока при любых действиях первого игрока. Поэтому направление оптимизации целевой функции
, которая минимизировала бы цену игры первого игрока при любых действиях первого игрока. Поэтому направление оптимизации целевой функции  . При этом, согласно теореме 3, применение первым вторым игроком оптимальной стратегии гарантирует проигрыш, не больший цены игры, то есть
. При этом, согласно теореме 3, применение первым вторым игроком оптимальной стратегии гарантирует проигрыш, не больший цены игры, то есть  (
( ). Объединяя полученные соотношения в систему, получаем ЗЛП второго игрока:
). Объединяя полученные соотношения в систему, получаем ЗЛП второго игрока:
|
|
|
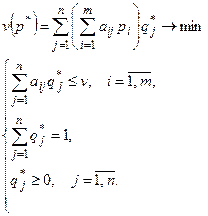
Коэффициентами целевой функции ЗЛП второго игрока являются величины  , которые меняются в зависимости от поведения первого игрока (меняется вектор
, которые меняются в зависимости от поведения первого игрока (меняется вектор  ).
).
Исключим величины  из ЗЛП второго игрока. Для этого, предполагая, что
из ЗЛП второго игрока. Для этого, предполагая, что  , разделим все соотношения системы ограничений на
, разделим все соотношения системы ограничений на 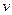 :
:
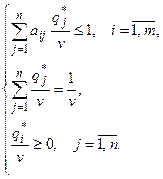
Выполним замену переменных:  (
( ). Так как
). Так как  , то
, то 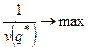 . Обозначим
. Обозначим  тогда ЗЛП второго игрока примет окончательный вид:
тогда ЗЛП второго игрока примет окончательный вид:
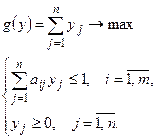
Таким образом, двойственная пара задач линейного программирования для парной  -игры с нулевой суммой имеет вид:
-игры с нулевой суммой имеет вид:
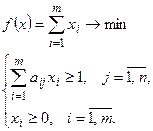
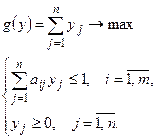
Достаточно решить одну из задач (более удобную), а затем найти решение второй задачи с помощью теорем двойственности (см. тетрадь № 2).
Решение исходно задачи ( -игры) находят с помощью обратной замены переменных (
-игры) находят с помощью обратной замены переменных ( и
и  – решения пары прямой и двойственной задач ЛП):
– решения пары прямой и двойственной задач ЛП):
 или
или 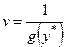 ,
,  (
( ),
),  (
( ).
).
Замечание 1. Если в исходной  -игре
-игре  , то игру преобразовывают в соответствии с теоремой 4 в игру с платёжной матрицей
, то игру преобразовывают в соответствии с теоремой 4 в игру с платёжной матрицей  , где число
, где число  . Такое преобразование позволит получить цену преобразованной игры
. Такое преобразование позволит получить цену преобразованной игры  .
.
Замечание 2. Если в исходной  -игре
-игре  , то при делении на
, то при делении на 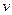 следует менять знак в неравенствах-ограничениях на противоположный.
следует менять знак в неравенствах-ограничениях на противоположный.
Игры с природой
Игры с природой – это специальный класс матричных игр, в которых одним из участников является человек или группа лиц, объединённых общностью цели (игрок А), а другим – «природа» (игрок П).
Под термином «природа» понимается весь комплекс внешних условий, при которых игроку А приходится принимать решение. Природа безразлична к выигрышу и не стремится обратить в свою пользу промахи игрока А.
Игрок А может использовать  стратегий
стратегий  ,
,  , …,
, …,  , а природа может реализовать
, а природа может реализовать  различных состояний
различных состояний  ,
,  , …,
, …,  . Игроку А могут быть известны вероятности
. Игроку А могут быть известны вероятности  , с которыми природа реализует свои состояния
, с которыми природа реализует свои состояния  . Действуя против природы, игрок А может пользоваться как чистыми
. Действуя против природы, игрок А может пользоваться как чистыми  , так и смешанными
, так и смешанными  стратегиями. Если он имеет возможность численно оценить (величиной
стратегиями. Если он имеет возможность численно оценить (величиной 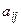 ) последствия применения каждой своей стратегии
) последствия применения каждой своей стратегии  при любом состоянии природы
при любом состоянии природы  , то игру можно задать платёжной матрицей
, то игру можно задать платёжной матрицей  .
.
При упрощении платёжной матрицы игры с природой имеется своя специфика: отбрасывать те или иные состояния природы (стратегии игрока П) нельзя, так как она может реализовать любое состояние независимо от того, выгодно оно или нет.
При выборе оптимальной стратегии игрока А пользуются различными критериями. При этом опираются как на платёжную матрицу, так и на матрицу рисков.
Определение. Риском  игрока А, когда он пользуется чистой стратегией
игрока А, когда он пользуется чистой стратегией  при состоянии
при состоянии  природы, называется разность между максимальным выигрышем
природы, называется разность между максимальным выигрышем  , который он мог бы получить, если бы достоверно знал, что природой будет реализовано именно состояние
, который он мог бы получить, если бы достоверно знал, что природой будет реализовано именно состояние  , и тем выигрышем
, и тем выигрышем 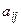 , который он получит, используя стратегию
, который он получит, используя стратегию  , не зная, какое же состояние
, не зная, какое же состояние  природа реализует.
природа реализует.
Таким образом, элементы матрицы рисков 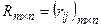 определяются по формуле
определяются по формуле  (
( – максимальный элемент
– максимальный элемент  -го столбца платёжной матрицы).
-го столбца платёжной матрицы).
Если вероятности  состояний
состояний  природы известны, то для определения оптимальных стратегий пользуются критериями Байеса и Лапласа.
природы известны, то для определения оптимальных стратегий пользуются критериями Байеса и Лапласа.
Критерий Байеса. В качестве оптимальной принимается чистая стратегия  , при которой максимизируется средний выигрыш
, при которой максимизируется средний выигрыш  (
( ) игрока А, то есть обеспечивается
) игрока А, то есть обеспечивается  .
.
Критерий Лапласа. Если игроку А представляются в равной мере правдоподобными все состояния  природы, то
природы, то  (
( ), и оптимальной считается чистая стратегия
), и оптимальной считается чистая стратегия  , обеспечивающая
, обеспечивающая  .
.
Если вероятности  состояний
состояний  природы неизвестны, то пользуются критериями Вальда, Сэвиджа, Гурвица.
природы неизвестны, то пользуются критериями Вальда, Сэвиджа, Гурвица.
Критерий Вальда. Оптимальной считается чистая стратегия  , при которой наименьший выигрыш
, при которой наименьший выигрыш  игрока А будет максимальным, т.е ему обеспечивается
игрока А будет максимальным, т.е ему обеспечивается  .
.
Для смешанных стратегий критерий Вальда формулируется так: оптимальной считается та смешанная стратегия  , при которой минимальный средний выигрыш игрока А
, при которой минимальный средний выигрыш игрока А 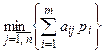 будет максимальным, то есть стратегия
будет максимальным, то есть стратегия  , найденная из условия
, найденная из условия  .
.
Критерий Сэвиджа. Оптимальной считается та чистая стратегия  , при которой минимизируется величина
, при которой минимизируется величина  максимального риска, то есть обеспечивается
максимального риска, то есть обеспечивается  .
.
Для смешанных стратегий критерий Сэвиджа формулируется так: оптимальной считается та смешанная стратегия  , при которой максимальный средний риск игрока А
, при которой максимальный средний риск игрока А 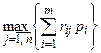 будет минимальным, то есть стратегия
будет минимальным, то есть стратегия  , найденная из условия
, найденная из условия  .
.
Критерий Гурвица. Оптимальной считается та чистая стратегия  , найденная из условия
, найденная из условия  , где число
, где число  выбирается из субъективных соображений.
выбирается из субъективных соображений.
Анализ практических ситуаций проводится по нескольким критериям одновременно, что позволяет глубже исследовать суть явления и выбрать наиболее обоснованное решение.
ПРАКТИКУМ
|
|
|


