 |
Упрощение платёжных матриц
|
|
|
|
Поиск оптимальных стратегий тем сложнее, чем больше размерность платёжной матрицы. Поэтому поиск оптимальных стратегий начинают с упрощения платёжной матрицы.
Определение 20. Если в платёжной матрице элементы  -ой строки не меньше соответствующих элементов
-ой строки не меньше соответствующих элементов 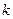 -ой строки, то есть
-ой строки, то есть  (
( ), то говорят, что стратегия
), то говорят, что стратегия  доминирует над стратегией
доминирует над стратегией 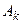 .
.
Определение 21. Если в платёжной матрице элементы 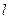 -го столбца не превосходят соответствующих элементов
-го столбца не превосходят соответствующих элементов  -го столбца, то есть
-го столбца, то есть 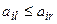 (
( ), то говорят, что стратегия
), то говорят, что стратегия  доминирует над стратегией
доминирует над стратегией  .
.
Определение 22. Стратегии  и
и 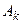 (
( и
и  ) называются дублирующими друг друга, если
) называются дублирующими друг друга, если 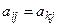 (
( ) (
) ( (
( )).
)).
Замечание. Дублирование является частным случаем доминирования. Игрокам выгоднее пользоваться доминирующими стратегиями. Поэтому вероятность применения доминируемых стратегий равна нулю. Исключая из платёжной матрицы доминируемые стратегии, можно уменьшить её размерность, что упрощает решение игры. При исключении доминируемых стратегий цена игры не меняется.
Теорема 4. Оптимальные смешанные стратегии  и
и  в игре с платёжной матрицей
в игре с платёжной матрицей 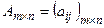 и ценой
и ценой 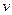 остаются оптимальными и для игры с платёжной матрицей
остаются оптимальными и для игры с платёжной матрицей  (
( ) и ценой
) и ценой 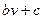 .
.
На основании теоремы 4 платёжную матрицу всегда можно преобразовать так, что её элементы будут целыми неотрицательными числами, что упрощает расчёты.
Пример 2.6 [2]. Найти решение игры, заданной платёжной матрицей:
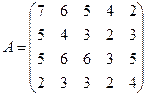 .
.
Решение. 1) Найдём верхнюю и нижнюю цены игры:
 ,
, 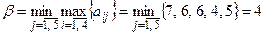 .
.
Так как  , то седловой точки в чистых стратегиях нет. Оптимальной стратегией первого игрока является стратегия
, то седловой точки в чистых стратегиях нет. Оптимальной стратегией первого игрока является стратегия  , так как в ней расположен максимин
, так как в ней расположен максимин  . Оптимальной стратегией второго игрока является стратегия
. Оптимальной стратегией второго игрока является стратегия  , так как в ней расположен минимакс
, так как в ней расположен минимакс  .
.
2) Исключим доминируемые (невыгодные) стратегии первого игрока. Так как все элементы строки  не превосходят элементов строки
не превосходят элементов строки  , то строку
, то строку  можно исключить. Аналогично, все элементы строки
можно исключить. Аналогично, все элементы строки 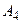 не превосходят элементов строки
не превосходят элементов строки  , поэтому исключаем и её. Строку
, поэтому исключаем и её. Строку  исключить нельзя, так как в ней есть элементы, превосходящие элементы строки
исключить нельзя, так как в ней есть элементы, превосходящие элементы строки  . Тогда преобразованная платёжная матрица игры будет иметь вид
. Тогда преобразованная платёжная матрица игры будет иметь вид  .
.
|
|
|
3) Исключим доминируемые стратегии второго игрока. Все элементы столбцов  ,
, 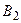 и
и  больше соответствующих элементов столбца
больше соответствующих элементов столбца  , поэтому эти столбцы можно исключить. В столбце
, поэтому эти столбцы можно исключить. В столбце 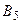 есть элементы, меньшие соответствующих элементов столбца
есть элементы, меньшие соответствующих элементов столбца  , поэтому этот столбец следует оставить. Преобразованная платёжная матрица игры будет иметь вид
, поэтому этот столбец следует оставить. Преобразованная платёжная матрица игры будет иметь вид  .
.
4) Найдём седловую точку матрицы  в смешанных стратегиях.
в смешанных стратегиях.
Пусть оптимальные стратегии игроков определяются, соответственно векторами вероятностей  ,
,  , компоненты которых удовлетворяют условию нормировки:
, компоненты которых удовлетворяют условию нормировки: 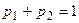 ,
,  .
.
Функция выигрыша будет иметь вид:

 .
.
Так как, согласно теореме о минимаксе, требуется найти максимум функции выигрыша, то должно быть 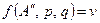 и, следовательно, должно выполняться равенство:
и, следовательно, должно выполняться равенство:  . Система уравнений для определения оптимальных стратегий
. Система уравнений для определения оптимальных стратегий  и
и  имеет вид:
имеет вид:
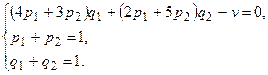
В ней содержится 3 уравнения и 5 неизвестных.
Для отыскания  и
и 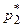 запишем:
запишем:  и
и  , тогда
, тогда 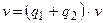 . Подставим полученное соотношение в первое уравнение системы, получим:
. Подставим полученное соотношение в первое уравнение системы, получим:  или
или  .
.
Так как по теореме 3 значения  и
и  должны быть отличны от нуля (как оптимальные), то последнее равенство выполняется при произвольных положительных
должны быть отличны от нуля (как оптимальные), то последнее равенство выполняется при произвольных положительных  и
и  только в том случае, когда
только в том случае, когда
 или
или  .
.
Так как 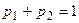 , то
, то 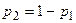 , и
, и  . Раскрывая скобки и выражая
. Раскрывая скобки и выражая  , получим
, получим  ,
,  .
.
Таким образом, вероятности оптимальных стратегий первого игрока  ,
,  .
.
Применяя аналогичный приём для отыскания  и
и  получаем, что так как
получаем, что так как  и
и 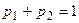 , то
, то  . Подставим это соотношение в первое уравнение системы, получим:
. Подставим это соотношение в первое уравнение системы, получим:
 .
.
Сгруппируем слагаемые в этом уравнении относительно  и
и  :
:
 .
.
Так как значения  и
и 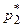 отличны от нуля, то последнее равенство выполняется только в том случае, когда
отличны от нуля, то последнее равенство выполняется только в том случае, когда
|
|
|
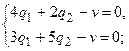 или
или  .
.
Так как  , то
, то 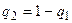 , и
, и  . Раскрывая скобки и выражая
. Раскрывая скобки и выражая  , получим
, получим  ,
,  .
.
Таким образом, вероятности оптимальных стратегий второго игрока  ,
,  .
.
Подставим найденные оптимальные вероятности смешанных стратегий в функцию выигрыша, найдём цену игры:

 .
.
Ответ:  при
при  и
и 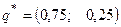 . Первый игрок может с одинаковыми вероятностями применять обе стратегии. Второму игроку выгоднее чаще использовать первую стратегию.
. Первый игрок может с одинаковыми вероятностями применять обе стратегии. Второму игроку выгоднее чаще использовать первую стратегию.
|
|
|


