Измерение связи между явлениями. Методы изучения корреляционных связей при оценке показателей здоровья и факторов окружающей среды.

Известны два вида связи между явлениями (признаками): функциональная и корреляционная. Функциональная связь отражает строгую зависимость процессов или явлений и изменение какого-либо одного явления обязательно связано с изменением числовых значений другого явления на строго определенную величину. Функциональная связь, как правило, проявляется при физических и химических явлениях, где её можно представить в виде уравнения, формулы. Примером функциональной связи может являться увеличение объема шара в строгой зависимости от увеличения его радиуса, расширение тела по мере увеличения температуры нагревания и т.д. Корреляция – понятие, которое также означает взаимосвязь между признаками. При корреляционных связях, характерных для медико-биологических явлений, значению одного признака соответствуют разные значения других признаков. Корреляционная связь необходима, например, при оценке взаимосвязей между стажем работы и уровнем заболеваемости работающих; между разными уровнями физических факторов окружающей среды и состоянием здоровья; между различными уровнями интенсивности нагрузки и частотой (уровнем) физиологических реакций организма; между сроками госпитализации и частотой осложнений. Статистика позволяет исследователю измерить связи, обосновать выводы и наглядно их иллюстрировать. Корреляционная связь бывает положительной - прямой (при увеличении одного признака увеличивается другой) и отрицательной - обратной (при увеличении одного показателя другой уменьшается). Коэффициент корреляции свидетельствует не только о направлении связи, но и об уровне этой связи.

Таблица 3

Схема оценки силы и направления корреляционной связи по коэффициенту корреляции

Сила связи	Направление связи
прямая (+)	обратная (-)
Сильная	от + 1 до +0,7	от - 1 до - 0,7
Средняя	от + 0,699 до + 0,3	от - 0,699 до - 0,3
Слабая	от + 0,299 до 0	от - 0,299 до 0

 

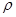Наиболее простыми методом определения коэффициента корреляции являются ранговая корреляция: , где - коэффициент ранговой корреляции, d - разность рангов, n – число сопоставляемых пар признаков.При ранговой корреляции числовые выражения сравниваемых статистических рядов ранжируют, то есть проставляют ранговые номера для каждой цифры (от 1 и далее) и подставляют значения в формулу с учетом разницы порядковых значений. При расчете коэффициента корреляции методом квадратов (метод Пирсона) сначала вычисляют среднее значение в каждом вариационном ряду сравниваемых групп. Затем находят отклонение каждой величины ряда от полученной средней. Для устранения отрицательных значений эти величины возводят в квадрат и подставляют в формулу: r_{xy =} , где d_x и d_y – отклонение каждой варианты от своей средней арифметической М_х и М_y. По величине коэффициента устанавливают направление и силу связи. Достоверность коэффициента определяют по таблицам критических значений (таблицам Каминского) при n´ = n-2, а также при расчете средней ошибки и критерия достоверности t. Коэффициент корреляции должен превышать свою ошибку не менее чем в 3 раза.Формула ошибки коэффициента ранговой корреляции: m = ± , t = 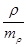По методу Пирсона ошибка коэффициента корреляции вычисляется по формуле: m_{r = ±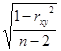} , t = 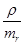. Значения t оценивается по таблице критических значений критерия t (при n<30, таблица критических значений критерия Стьюдента t).Таблица 4

Значения критерия Стьюдента t при числе наблюдений больше 30

Величина критерия Стьюдента t	Вероятность безошибочного прогноза
в единицах	в процентах
1,0	0,6827	68,3
1,5	0,8664	86,6
2,0	0,9545	95,5
2,5	0,9876	98,8
3,0	0,9973	99,7
3,5	0,9995	99,95
4,0	0,9999	99,99

Таблица 5

Таблица критических значений критерия Стьюдента t

при числе наблюдений <30

Число степеней свободы = n - 1	Уровень вероятности безошибочного прогноза (в %)
		99.9
	12,7	63,6	636,6
	4,3	9,9	31,6
	3,1	5,8	12,9
	2,7	4,6	8,6
	2,5	4,0	6,8
	2,4	3,7	5,9
	2,3	3,5	5,4
	2,3	3,3	5.1
	2,2	3,2	4,7
	2.2	3,1	4,6
	2,2	3,1	4,4
	2,2	3,0	4,3
	2,1	3,0	4,2
	2,1	2,9	4,1
	2,1	2.9	4,0
	2,1	2,9	4,0
	2,1	2,8	3,9
	2,1	2,8	3,9
	2,0	2,8	З,8
	2,0	2,8	3,8
	2,0	2,8	3,8
22	2,0	2,8	3,7
	2,0	2,8	3.7
	2,0	2,7	3,7
	2.0	2.7	3,7
	2,0	2,7	3,7
	2,0	2.7	3,6
	2,0	2,7	3,6
	2,0	2.7	3,6
	2,0	2,7	3,6

Таблица 6

Стандартные коэффициенты корреляции, считающиеся достоверными

(по Л.С. Каминскому)

Число степеней свободы п ' = п — 2	Уровень вероятности наличия связи р (%)	Число степеней свободы п' = п — 2	Уровень вероятности наличия связи р (%)
95,0	98,0	99,0	95.0	98,0	99,0
	0,997	0,999	0,999		0,532	0,612	0,661
	0,950	0,980	0,990		0,514	0,592	0,641
	0,878	0,934	0,959		0,497	0,574	0,623
	0,811	0,882	0,917		0,482	0,558	0,606
	0,754	0,833	0,874		0,468	0,542	0,590
	0,707	0,789	0,834		0,456	0,528	0,575
	0,666	0,750	0,798		0,444	0,516	0,561
	0,632	0,716	0,765		0,433	0,503	0,549
	0,602	0,685	0,735		0,423	0,492	0,537
	0,576	0,658	0,708		0,381	0,445	0,487
	0,553	0,634	0,684		0,349	0,409	0,449

Тема 7

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: