 |
Устойчивость многомерных стационарных систем
|
|
|
|
В прошлом семестре мы рассматривали устойчивость одномерных САУ, которые имели одну входную и одну выходную величину. Связь между входом и выходом описывалась линейным дифференциальным уравнением n-го порядка.
Рассмотрим систему, которая имеет m входов и n входов и которая описывается системой линейных дифференциальных уравнений с постоянными коэффициентами.
В общем случае эти уравнения имеют вид:
(1)
.
.
Если использовать векторно-матричную форму записи, то система (1) запишется
(2)
Для системы (1) или (2) так же, как и для одномерных систем, можно ввести понятие устойчивости номинального режима.
Пусть номинальный режим в системе (1) или (2) характеризуется входными сигналами:
и номинальными начальными условиями
При этих входных сигналах и начальных условиях существует номинальный режим, который обозначим
Обычно бывает трудно поддерживать номинальные начальные условия и в системе существуют реальные начальные условия («отклоненные» начальные условия)
При отклоненных начальных условиях и тех же номинальных входных воздействиях в системе устанавливается «отклоненный» номинальный режим
Запишем систему уравнений (1) для номинального режима и номинальных начальных условий
(3) 
Запишем систему уравнений (1), соответствующую «отклоненным» начальным условиям и тем же входным воздействиям:
(4) 
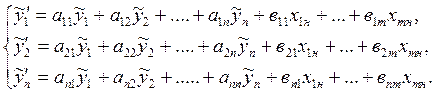
Обозначим 
Номинальный режим 
будем называть асимптотически устойчивым, если достаточно малым значениям отклонений начальных условий соответствуют для любого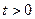 
достаточно малые отклонения 
и 
Положим 
Тогда уравнение (4) запишется:
(5)
Запишем систему уравнений для отклонений 
Для этого из уравнений (5) вычтем почленно систему уравнений (3)
|
|
|
(6) 
или в векторно-матричной форме
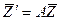(7)
Если все координаты 
системы (6) будут малы и , то номинальный режим системы (1) будет асимптотически устойчивым.
Поскольку система уравнений (6) или (7) не зависят от входных воздействий, то будут одновременно устойчивы или неустойчивы все номинальные режимы системы (1).
Таким образом, для линейных многомерных систем, так же как и для линейных одномерных систем, можно говорить не об устойчивости номинальных режимов, а об устойчивости системы (т.е, если система устойчива, то устойчивы все ее номинальные режимы)
Как известно из курса дифференциальных уравнений общее решение однородного дифференциального уравнения (6) (системы линейных уравнений) определяется корнями характеристического уравнения, т.е. 
(8)
где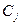 
- константы, зависящие от начальных условий, 
- корни характеристического уравнения.
Характеристическое уравнение для нахождения корней для системы (6) имеет вид:
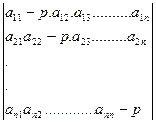(9)
Для нахождения корней надо расписать определитель (9), получится уравнение 
ой степени, по которому и определяются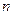 
корней.
Из уравнения (8) следует, что если вещественная часть корней 
, то система (6) асимптотически устойчива.
Пример.
Исследовать устойчивость многомерной системы
Система многомерная, т.к у нее 2 выхода, хотя вход один.
Запишем уравнения в отклонениях от номинального режима
Здесь нет Хi , , т.к. это входные воздействия, а они вычитаются.
Составим определитель
Согласно критерию Гурвица, система второго порядка устойчива, если все ее коэффициенты положительны.
Следовательно, исходная многомерная система будет устойчива.
Запись дифференциальных уравнений в векторно-матричной форме
(через переменные состояния)
Иногда при описании динамики САУ используют переменные состояния - это внутренние часто недоступные переменные, которые определяют состояние объекта в каждый момент времени t.
|
|
|
Здесь U1….Um - управляющие воздействия, т.е переменные, влияющие на поведение объекта, 
, (U – принадлежит m -мерному вещественному линейному пространству)
У1…..Уn – выходные переменные, их можно измерять и они отображают реакцию объекта на управляющее воздействие, 
,
Х1….Хn - переменные состояния, 
, 
,
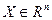F1….Fi - возмущающие воздействия, 
.
Запишем уравнения многомерного объекта через переменные состояния:
(1) - это дифференциальные уравнения состояния,
(2) – выходные переменные объекта, записанные через переменные состояния.
, 
, 
.
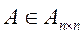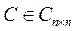Для описания одномерного объекта обычно используют скалярное дифференциальное уравнение
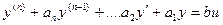(3)
Это уравнение можно привести к виду (1) и (2) после выбора линейно-независимых переменных состояния. Их число всегда равно порядку объекта (n), а 
, и 
Наиболее простое описание получается в случае, когда в качестве переменных состояния берется выходная величина у и ее производные до (n-1) порядка включительно. При этом вместо уравнения (3) для одномерного объекта имеем:
(Пояснения:
если задано диф. уравнение
тогда 
и 
и в форме Коши
)
При этом
, 
. 
.
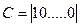Переход от (1) и (2) к (3) не является однозначным: для одного объекта можно выбрать бесконечное множество наборов переменных состояния, важно только, чтобы они были линейно-независимы.
При этом каждой совокупности переменных состояния будут соответствовать свои матрицы А,В,С.
Пример. (для Госэкзамена)
Система описана дифференциальными уравнениями в форме Коши
Необходимо записать их в векторно-матричной форме
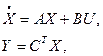получив матрицы А,В,СТ.
Ответ:
, 
, 
.
|
|
|
