 |
Приближенные методы исследования нелинейных САУ
|
|
|
|
Метод гармонического баланса
При исследовании НЛ САУ иногда можно наблюдать появление периодических изменений выходной величины у(t) даже в тех случаях, когда 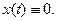 Если при изучении САУ ограничиться линейной моделью с постоянными коэффициентами, то указанное явление (собственные колебания) может иметь место только при наличии в характеристическом уравнении чисто мнимых корней
Если при изучении САУ ограничиться линейной моделью с постоянными коэффициентами, то указанное явление (собственные колебания) может иметь место только при наличии в характеристическом уравнении чисто мнимых корней  .
.
Однако при таком объяснении малое изменение параметров системы «сдвинет» корень с мнимой оси налево или направо и собственные колебания либо затухают либо раскачиваются. На практике же в нелинейных системах периодические колебания выходного сигнала сохраняются при малых изменениях параметров системы.
Такого рода незатухающие колебания объясняются нелинейным характером системы. Они называются автоколебаниями.
Рассмотрим метод гармонического баланса, который позволяет по взаимному протеканию АФЧХ линейной части и и характеристики нелинейного элемента определить наличие или отсутствия автоколебаний.
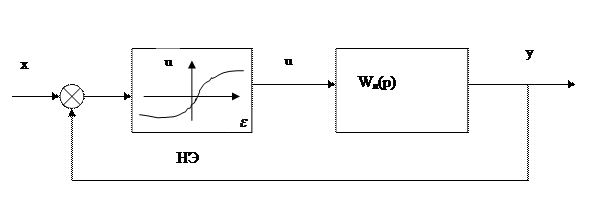
Рассмотрим одноконтурную систему, в которой выделяется нелинейный элемент
 (1)
(1)
и линейная часть с передаточной функцией 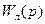 .
.

Рис.1
Предполагается:
1. 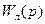 соответствует устойчивой системе,
соответствует устойчивой системе,
2. нелинейная характеристика  - нечетная симметричная, т.е.
- нечетная симметричная, т.е.
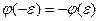 ,
,
3.входной сигнал  , т.е. это система стабилизации.
, т.е. это система стабилизации.
Будем искать выходной сигнал у(t) в виде
 , (2)
, (2)
где 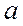 - амплитуда автоколебаний,
- амплитуда автоколебаний,
 - частота автоколебаний.
- частота автоколебаний.
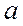 и
и  надо определить.
надо определить.
Гипотеза о синусоидальном характере у(t) выглядит произвольной. Однако далее будут приведены условия, при выполнении которых эта гипотеза становится естественной.
Поскольку  ,
, 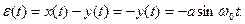 (3)
(3)
Пропустим сигнал  последовательно через нелинейный элемент и линейную часть и найдем уравнения, их которых можно будет определить амплитуду
последовательно через нелинейный элемент и линейную часть и найдем уравнения, их которых можно будет определить амплитуду  и частоту
и частоту  автоколебаний в НЛ САУ.
автоколебаний в НЛ САУ.
|
|
|
Прохождение  через линейный элемент
через линейный элемент
Так как  - периодическая функция, то сигнал
- периодическая функция, то сигнал 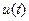 на выходе нелинейногоэлементатакже будет периодической функцией, но отличной от синусоиды.
на выходе нелинейногоэлементатакже будет периодической функцией, но отличной от синусоиды.

Спектр  Спектр
Спектр 


Как известно, любая периодическая функция может быть представлена рядом Фурье:
 (4)
(4)
Мы предполагаем, что свободный член в формуле (4) равен нулю. Это будет иметь место, например, когда характеристика нелинейного элемента удовлетворяет условию

 , т.е это нечетная функция.
, т.е это нечетная функция.
Здесь коэффициенты Фурье  и
и  определяются:
определяются:
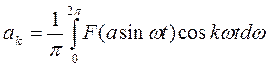 ,
,
 (5)
(5)
Преобразуем (4), умножив и поделив каждый член в правой части на  (6)
(6)


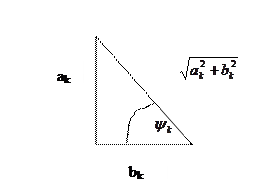
(7)
Получим

 .
.
Напомним, что 

 (8)
(8)
Таким образом при прохождении сигала  через нелинейный элемент, на выходе нелинейного элемента сигал
через нелинейный элемент, на выходе нелинейного элемента сигал  содержит множество гармоник, кратных
содержит множество гармоник, кратных  . (см. рисунок выше).
. (см. рисунок выше).
Прохождение сигнала  через линейную часть
через линейную часть
Из теории линейных систем мы знаем, что если на вход линейного звена с передаточной функцией 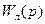 , соответствующей устойчивой системе, подать гармонический сигнал
, соответствующей устойчивой системе, подать гармонический сигнал  то в установившемся режиме на выходе этого звена будет сигнал
то в установившемся режиме на выходе этого звена будет сигнал  .
.
Здесь  - модуль частотной характеристики
- модуль частотной характеристики 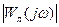 в точке
в точке  ,
,
 аргумент
аргумент  .
.
Используя эти соотношения, мы можем выписать выражения для  , пропуская по отдельности через линейную часть все составляющие ряда (8) и суммируя затем полученные выражения для
, пропуская по отдельности через линейную часть все составляющие ряда (8) и суммируя затем полученные выражения для 
В силу линейности системы такая процедура законна.
Получим, полагая 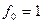 :
:
 (9)
(9)
Полученное выражение (9) для  имеет достаточно сложную структуру. Его можно существенно упростить, используя гипотезу фильтра.
имеет достаточно сложную структуру. Его можно существенно упростить, используя гипотезу фильтра.
Изучая частотные характеристики типовых элементарных звеньев, мы видели, что их АЧХ стремятся к нулю при 
Гипотеза фильтра состоит в том, что АЧХ в правой части (9) убывает с ростом частоты настолько быстро, что в (9) можно учитывать лишь первый член, соответствующий к=1, и считать остальные члены пренебрежимо малыми. Другими словами – гипотеза фильтра – это гипотеза о том, что линейная часть САУ практически не пропускает высокочастотные колебания. Поэтому формула (9) (и в этом состоит приближенность метода) упрощается следующим образом:
|
|
|
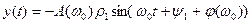 (10)
(10)
Таким образом, при замыкании системы в предположении гипотезы фильтра мы получим баланс гармоник (отсюда и название метода – метод гармонического баланса)

Рассмотрим как с помощью метода гармонического баланса определить амплитуду а и частоту  автоколебаний.
автоколебаний.
Введем понятие эквивалентной передаточной функции нелинейного элемента:
 (11)
(11)
Если 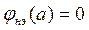 (а это имеет место при однозначных симметричных нелинейных характеристиках), то
(а это имеет место при однозначных симметричных нелинейных характеристиках), то
 (12)
(12)
Характеристическое уравнение замкнутой САУ (рис.1) имеет вид:

или частотная характеристика
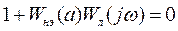 (13)
(13)
Отсюда
 (14)
(14)
Представим

Тогда

 (16)
(16)
Тогда уравнение (14) перепишется:
 =
=  (17)
(17)
Равенство (14) или (17) является основой графо-аналитического метода определения параметров автоколебаний а и  .
.
На комплексной плоскости строится АФЧХ линейной части

и характеристика нелинейного элемента


Если кривые пересекаются, то в САУ существуют автоколебания.
Частота автоколебаний в точке пересечения кривых по  , а амплитуда- по
, а амплитуда- по  .
.
Рассмотрим подробнее выделенный участок

Мы знаем амплитуду и частоту точек, ближайших к точке пересечения кривых. Амплитуду и частоту в точке пересечения можно определить, например, методом деления отрезка пополам.
Метод гармонической линеаризации
Это очень эффективный приближенный метод определения периодических колебаний в НЛ САУ.
Для применения метода гармонической линеаризации нелинейности необходимо выполнение требования – линейная часть должна обладать свойствами фильтра, т.е. она не должна пропускать высокие частоты.
На практике это требование обычно выполняется.

Пусть имеется нелинейный элемент
 (1)
(1)
Пусть 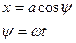 (2)
(2)
Тогда  (3)
(3)
Разложим (1) в ряд Фурье:
Напомним, нелинейная функция F(x), разложенная в ряд Фурье, имеет вид:
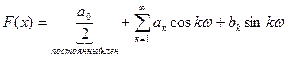 ,
,
где
 ,
,  ,
, 
Тогда ряд Фурье для нашей нелинейности будет иметь вид:

 +
+ 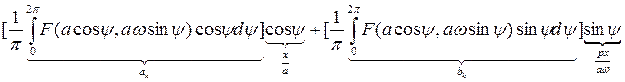 +высшие гармоники (4)
+высшие гармоники (4)
Положим постоянную составляющую 
|
|
|
Из уравнения (2): 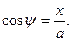
Из уравнения (3): 
Тогда уравнение (4) можно переписать:
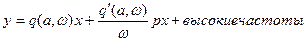 (5)
(5)
 ,
,

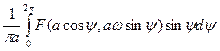
В уравнении (5) пренебрегаем высокими частотами и в этом приближенность метода.
Таким образом, нелинейный элемент при  заменяется линеаризованным выражением (5), которое при выполнении гипотезы фильтра линейной части принимает вид:
заменяется линеаризованным выражением (5), которое при выполнении гипотезы фильтра линейной части принимает вид:
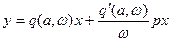 (6)
(6)
Эта процедура называется гармонической линеаризацией.
Коэффициенты  и
и  при постоянных а и
при постоянных а и  . В динамическом же режиме, когда изменяются а и
. В динамическом же режиме, когда изменяются а и  , коэффициенты
, коэффициенты  и
и  будут изменяться. В этом отличие гармонической линеаризации от обычной. (При обычной линеаризации коэффициент линеаризованного уравнения К зависит от точки линеаризации). Зависимость коэффициентов линеаризации от а и
будут изменяться. В этом отличие гармонической линеаризации от обычной. (При обычной линеаризации коэффициент линеаризованного уравнения К зависит от точки линеаризации). Зависимость коэффициентов линеаризации от а и  позволяет применить к НЛ САУ (6) методы исследования линейных систем и анализировать свойства НЛ САУ, которые не могут быть обнаружены при обычной линеаризации.
позволяет применить к НЛ САУ (6) методы исследования линейных систем и анализировать свойства НЛ САУ, которые не могут быть обнаружены при обычной линеаризации.
Коэффициенты гармонической линеаризации
некоторых типовых нелинейностей
1. Релейная характеристика



2.Релейная характеристика с зоной нечувствительности

 ,
,  Амплитуда колебаний
Амплитуда колебаний 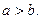
3.Релейная характеристика с петлей гистерезиса

 ,
, 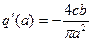 ,
, 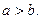
4.Релейная характеристика с зоной нечувствительности и петлей гистерезиса

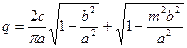 ,
, 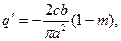


Теперь рассмотрим замкнутую систему.
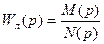 ,
,
Можно ввести понятие передаточной функции нелинейного элемента
 ,
,
тогда
 .
.
Тогда характеристическое уравнение замкнутой САУ:
 ,
,
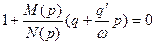 или
или
 (7)
(7)
Когда в замкнутой системе возникают собственные незатухающие колебания постоянной амплитуды и частоты, то коэффициенты гармонической линеаризации становятся постоянными и САУ становится линейной. А в линейной системе наличие периодических незатухающих колебаний говорит о наличии у нее чисто мнимых корней.
Таким образом для определения периодических решений надо в характеристическое уравнение подставить  . Здесь
. Здесь  - текущая частота, а
- текущая частота, а  - частота автоколебаний.
- частота автоколебаний.


В этом уравнении неизвестными являются  и
и  .
.
Выделим в этом уравнении действительную и мнимую части.

Введем для частоты и амплитуды искомого периодического решения обозначения  ,
,  .
.
|
|
|
Получим два уравнения с двумя неизвестными.

Решив эти уравнения, найдем 
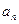 и
и 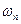 - амплитуду и частоту периодических решений в НЛ САУ.
- амплитуду и частоту периодических решений в НЛ САУ.
С помощью этих уравнений можно определить не только 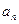 и
и 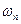 , но и построить зависимость
, но и построить зависимость 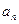 и
и 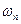 , например, от коэффициента усиления САУ К.
, например, от коэффициента усиления САУ К.
Тогда, считая К переменным, запишем:
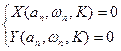
Задаваясь К, находим 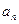 и
и 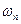 , т.е
, т.е 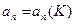 и
и 

Можно выбрать К так, чтобы
1. 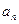 было бы мало,
было бы мало,
2. 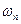 было бы неопасно для САУ,
было бы неопасно для САУ,
3.автоколебаний не было бы.
С помощью этих же уравнений можно на плоскости двух параметров (например, Т и К) построить линии равных значений амплитуды и частоты автоколебаний. Для этого уравнения переписывают:

Задаваясь числовыми значениями 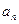 , получим
, получим  и
и 

По этим графикам можно выбирать Т и К.
Определение устойчивости решений в нелинейных САУ
Автоколебаниям в НЛ САУ должны соответствовать устойчивые периодические решения. Поэтому после нахождения амплитуды 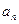 и частоты
и частоты 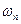 периодических решений необходимо исследовать их на устойчивость.
периодических решений необходимо исследовать их на устойчивость.
Рассмотрим приближенный метод исследования устойчивости периодических решений в НЛ САУ с помощью годографа Михайлова.
Пусть НЛ САУ

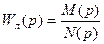 ,
,  .
.  - получена с помощью метода гармонической линеаризации.
- получена с помощью метода гармонической линеаризации.
Характеристическое уравнение замкнутой системы

Запишем уравнение характеристической кривой (годографа Михайлова), для чего подставим в него  .
.
 - текущее значение частоты вдоль годографа Михайлова,
- текущее значение частоты вдоль годографа Михайлова,
 - частота гармонической линеаризации (автоколебаний).
- частота гармонической линеаризации (автоколебаний).
Тогда для любых заданных постоянных  и
и  кривая Михайлова будет иметь такой же вид, как и для обыкновенных линейных систем.
кривая Михайлова будет иметь такой же вид, как и для обыкновенных линейных систем.
При периодических решениях, соответствующих 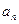 и
и 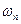 , годограф Михайлова будет проходить через начало координат (т.к. система находится на границе устойчивости).
, годограф Михайлова будет проходить через начало координат (т.к. система находится на границе устойчивости).

Для определения устойчивости периодических решений дадим 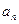 приращение
приращение 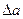

Если при  кривая Михайлова займет положение 1, а при
кривая Михайлова займет положение 1, а при
 - положение 2, то периодическое решение устойчиво.
- положение 2, то периодическое решение устойчиво.
Если при  кривая займет положение 2, а при
кривая займет положение 2, а при  - положение 1, то периодическое решение неустойчиво.
- положение 1, то периодическое решение неустойчиво.
|
|
|


