 |
Улучшение качества процессов регулирования
|
|
|
|
Качество процессов регулирования определяется не только точностью на установившихся режимах работы, но и динамическими характеристиками переходных процессов, такими как длительность переходных процессов (быстродействие), колебательность и т.п. А эти динамические характеристики определяются запасом устойчивости системы, следовательно, надо увеличивать запас устойчивости.
Для повышения запаса устойчивости надо сначала попытаться изменить параметры системы (коэффициенты передачи отдельных звеньев, их постоянные времени). Если эти меры не помогают, надо идти на изменение структуры САУ, вводя в систему корректирующие устройства, которые должны изменить динамику САУ в нужном направлении.
Если корректирующее устройство (звенья) используется для придания системы устойчивости, увеличения запаса устойчивости, они называются демпфирующими или стабилизирующими. Термин корректирующие звенья- более широкий, они вводятся для изменения динамических свойств САУ.
Корректирующие звенья могут быть:
1. Последовательного типа

 (1)
(1)
2. Параллельного типа

 (2)
(2)
3. В виде местной обратной связи

 (3)
(3)
Использование вида корректирующих звеньев определяется удобством технической реализации. Корректирующие звенья можно заменять одно другим так, что их динамические свойства будут оставаться неизменными, т.е. 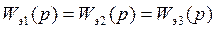 (4)
(4)
Если
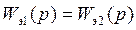
 =
=  , отсюда
, отсюда
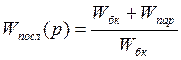 (5)
(5)
Если
 ,то
,то
 =
=  , отсюда
, отсюда

 (6)
(6)
Аналогично можно получить:
 (7)
(7)
 (8)
(8)

 (9)
(9)
 (10)
(10)
Последовательные корректирующие звенья удобно применять там, где в регуляторе используется электрический сигнал. В этом случае корректирующее звено 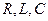 -цепочки.
-цепочки.
Корректирующие звенья параллельного типа удобно применять в тех случаях, когда необходимо осуществить сложный закон управления с введением интеграла и производных от сигнала ошибки.
|
|
|
Корректирующие звенья в виде местной обратной связи нашли наиболее широкое распространение. Особенно отрицательные обратные связи, т.к. они ослабляют влияние нестабильности параметров, влияние нелинейностей.
Последовательные корректирующие звенья.
Это обычно пассивные (не содержат источников энергии) электрические цепи.
Рассмотрим примеры идеальных последовательных корректирующих звеньев и их характеристики.
Дифференцирующее звено.

Дифференциальное уравнение
 ,
,
здесь  - постоянная времени дифференцирования,
- постоянная времени дифференцирования,
 - постоянная времени, характеризующая собственные динамические погрешности звена,
- постоянная времени, характеризующая собственные динамические погрешности звена,
т.к. 
 , то
, то 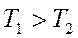 !!!!!
!!!!!
 - коэффициент усиления звена.
- коэффициент усиления звена.
 Передаточная функция дифференцирующего звена:
Передаточная функция дифференцирующего звена:
 .
.
Член  (или
(или  ) осуществляет дифференцирование входного сигнала, причем на выходе имеется производная от входного сигнала, но и сам входной сигнал.
) осуществляет дифференцирование входного сигнала, причем на выходе имеется производная от входного сигнала, но и сам входной сигнал.
Правая часть дифференциального уравнения (или знаменатель передаточной функции) характеризует собственные динамические погрешности звена (его инерционные свойства).
Проанализируем соотношения этих эффектов.
 . Это означает, что собственные динамические погрешности малы, а эффект дифференцирования – сильный.
. Это означает, что собственные динамические погрешности малы, а эффект дифференцирования – сильный.
 - коэффициент усиления маленький, т.е. происходит ослабление входного сигнала.
- коэффициент усиления маленький, т.е. происходит ослабление входного сигнала.
На установившемся режиме 
Как работает дифференцирующее звено.
На низких частотах: сопротивление  - велико и низкие частоты через большое сопротивление плохо передаются на выход, т.е. коэффициент передачи дифференцирующей цепочки на низких частотах мал. Таким образом в спектре выходного сигнала низкие частоты имеют очень маленькие амплитуды. Вспомним, что низкие частоты определяют установившееся состояние. Следовательно, установившееся значение- сигал низкой величины. (Это видно и из соотношения
- велико и низкие частоты через большое сопротивление плохо передаются на выход, т.е. коэффициент передачи дифференцирующей цепочки на низких частотах мал. Таким образом в спектре выходного сигнала низкие частоты имеют очень маленькие амплитуды. Вспомним, что низкие частоты определяют установившееся состояние. Следовательно, установившееся значение- сигал низкой величины. (Это видно и из соотношения  )
)
|
|
|
На высоких частотах: сопротивление  -мало и на выход проходят высокие частоты. Вспомним, что высокие частоты определяют фронт переходного процесса, т.е. увеличивают быстродействие процесса.
-мало и на выход проходят высокие частоты. Вспомним, что высокие частоты определяют фронт переходного процесса, т.е. увеличивают быстродействие процесса.
Таким образом, дифференцирующие цепочки подавляют низкие частоты и уменьшают установившееся значение выходной величины, т.е. уменьшают коэффициент усиления. С другой стороны, они увеличивают коэффициент передачи по высоким частотам и, следовательно, увеличивают быстродействие. Кроме того, дифференцирующие цепочки вносят положительный фазовый сдвиг, что повышает запас устойчивости.
Интегрирующее корректирующее звено.

Дифференциальное уравнение:

Передаточная функция

 ,
,
 .
.
В интегрирующем звене  !!!!
!!!!
Коэффициент усиления в интегрирующем звене изменяется по частотам. 
Для пояснения работы этой цепочки рассмотрим её частотную характеристику


На частотах, где  (т.е на частотах
(т.е на частотах  и этим членом по сравнению с 1 в знаменателе можно пренебречь. Так как
и этим членом по сравнению с 1 в знаменателе можно пренебречь. Так как  , то член
, то член  и подавно меньше единицы и
и подавно меньше единицы и  . Т.о. на
. Т.о. на  -это усилительное звено.
-это усилительное звено.
На частотах  (это низкие частоты) член
(это низкие частоты) член 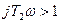 и в члене
и в члене  уже можно пренебречь 1 и рассматривать
уже можно пренебречь 1 и рассматривать  =
=  , т.е как интегрирующее звено. А т. к.
, т.е как интегрирующее звено. А т. к.  , то на этих частотах
, то на этих частотах 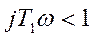 и числитель равен 1.
и числитель равен 1.
На частотах  (это более высокие частоты) член
(это более высокие частоты) член  и в члене
и в члене 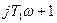 можно пренебречь 1 и в числителе появляется дифференцирующее звено.
можно пренебречь 1 и в числителе появляется дифференцирующее звено.
Таким образом в диапазоне 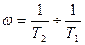 - это интегрирующее звено, а в диапазоне
- это интегрирующее звено, а в диапазоне  кроме интегрирования появляется эффект дифференцирования.
кроме интегрирования появляется эффект дифференцирования.
Напомним, что интегрирующее звено вносит фазовый сдвиг  , что плохо влияет на устойчивость. Вводится интегрирующее звено для повышения точности на установившемся режиме.
, что плохо влияет на устойчивость. Вводится интегрирующее звено для повышения точности на установившемся режиме.
Параллельные корректирующие звенья
Как отмечалось, они вводятся при сложных законах управления с использованием интеграла и производной от ошибки.
Введение интеграла приводит к уменьшению установившейся ошибки, введение производной – повышает запас устойчивости.
Например,




В этих примерах – дифференцирование- идеальное.
Введение параллельных дифференцирующих устройств способствует поднятию высоких частот (т.к. сопротивление емкости на в.ч. – мало), а, следовательно, это улучшает динамику САУ.
|
|
|
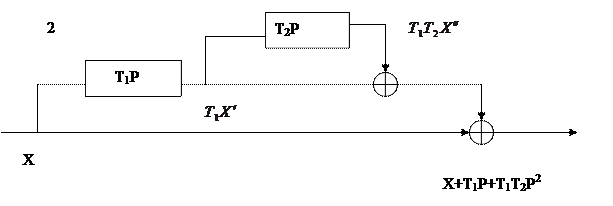
Примером параллельного корректирующего устройства служит изодромное устройство.

Интегрирующее звено повышает точность на установившемся режиме, дифференцирующее звено – повышает коэффициент усиления на высоких частотах, что приводит к улучшению динамических свойств САУ.
Обратные связи.
Обратные связи могут быть положительными и отрицательными, а также жесткими и гибкими. Гибкая обратная связь (ГОС). ГОС называется такая связь, которая действует только в переходных режимах, а на установившемся
режиме как бы отключается. 

На установившемся режиме  ,
,  и
и  .
.
Пример ГОС.


 .
.
На установившемся режиме  и
и  , как и в исходном апериодическом звене. Т.е. эта связь будет гибкой.
, как и в исходном апериодическом звене. Т.е. эта связь будет гибкой.
Жесткая обратная связь. (ЖОС)
Она действует не только в переходном режиме, но и в установившемся.


 =
= 

На установившемся режиме  и
и  , т.е. ЖООС действует и на установившемся режиме.
, т.е. ЖООС действует и на установившемся режиме.
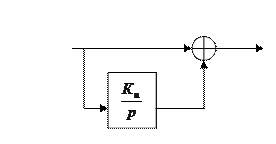
Если ЖООС – идеальное безинерционное звено, то
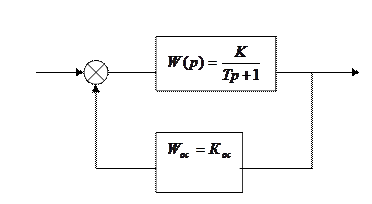

 .
.
ЖООС уменьшает постоянную времени и коэффициент усиления в  раз.
раз.
Расчетным путем наиболее просто определить параметры последовательного корректирующего звена, а реализовать проще обратные связи.
Положительные обратные связи (ПОС) находят меньшее использование, чем ООС.
 =
=  .
.
Если  , то
, то


Это изодромное звено, а оно, как известно, повышает астатизм системы. При этом в систему включено не интегрирующее звено, а инерционное, что меньше снижает запас устойчивости.
Однако, здесь точное выполнение  затруднено.
затруднено.
Синтез САУ
До сих пор мы в основном изучали задачу анализа САУ, когда математическая модель замкнутой САУ считалась заданной, и требовалось определить качество её работы: устойчивость, точность воспроизведения входного сигнала и т.п.
Важной, и более сложной, является задача синтеза, когда заданными считаются математическая модель управляемого объекта (и может быть измерительного и исполнительного устройств). Требуется выбрать структуру САУ, закон управления и числовые значения параметров регулятора, определяющие желаемое качество САУ.
|
|
|
С задачами синтеза мы уже встречались. Синтез САУ можно проводить, используя критерии устойчивости, Д-разбиение, методы корневых годографов.
Синтез одномерных одноконтурных САУ с единичной ООС с помощью ЛАФЧХ разомкнутой системы
Этот метод использует тесную связь между переходной функцией замкнутой САУ при ступенчатом воздействии и вещественной частью частотной характеристики замкнутой САУ.
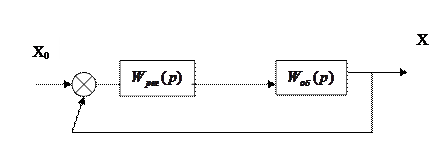
 , здесь
, здесь  . (1)
. (1)
 .
.
Т.о. по частотным характеристикам разомкнутой системы можно определить частотные характеристики замкнутой системы и наоборот. Имеются номограммы, связывающие эти частотные характеристики.
По  мы можем оценить переходный процесс (см. (1)).Таким образом, зная
мы можем оценить переходный процесс (см. (1)).Таким образом, зная 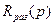 , мы можем оценить переходный процесс в системе.
, мы можем оценить переходный процесс в системе.
Решать задачу синтеза САУ по частотным характеристикам удобнее, когда частотные характеристики построены в логарифмическом масштабе.
В логарифмическом масштабе по оси ординат у откладывается  в дб.
в дб.



 увеличение этого соотношения в 10 раз соответствует увеличению
увеличение этого соотношения в 10 раз соответствует увеличению 
По оси абсцисс откладывается частота в логарифмическом масштабе.
Декада – изменение частоты в 10 раз.

Главное преимущество построения частотных характеристик в логарифмическом масштабе состоит в том, что их можно строить приближенно, практически без вычислений.
Возьмем инерционное звено. Его передаточная функция  ,
,
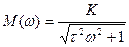 -АЧХ. Частота, где
-АЧХ. Частота, где  , т.е.
, т.е.  - частота сопряжения.
- частота сопряжения.
При приближенном построении ЛАЧХ:
1) 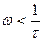 в
в  пренебрегаем
пренебрегаем  и
и 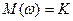 , а
, а 
 дБ
дБ
2)  в
в  пренебрегаем 1 и
пренебрегаем 1 и  и в логарифмическом масштабе
и в логарифмическом масштабе

Определим наклон при  :
:





 .
.
Наклон= 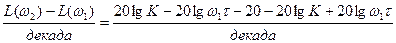 = - 20дб/дек.
= - 20дб/дек.
Следовательно, строя АЧХ в логарифмическом масштабе, можно убывающую часть характеристики заменить прямой с наклоном - 20дб/дек. Наибольшая погрешность будет в точке изгиба ( ).
).

Интегрирующее звено.
 ,
,  ,
, 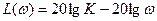 , при
, при 
 .
.
Наклон:

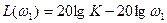


Наклон=  - 20 дб/дек
- 20 дб/дек

Аналогично можно показать, что у дифференцирующего звена наклон будет + 20 дб/дек.
Рассмотрим сначала на примере принцип построения приближенной ЛАЧХ (ФЧХ рассчитываются точно по формулам).
Приближенность построения ЛАЧХ заключается в том, что в частотной характеристике в членах  :
:
1) при  пренебрегают членом
пренебрегают членом 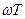 и звено рассматривают как усилительное
и звено рассматривают как усилительное  ;
;
2) при  пренебрегают 1 и рассматривают их как интегрирующее звено с частотной характеристикой
пренебрегают 1 и рассматривают их как интегрирующее звено с частотной характеристикой 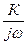 , наклон характеристики которого – 20 дб/дек и при
, наклон характеристики которого – 20 дб/дек и при  величина амплитуды равна 20lgK.
величина амплитуды равна 20lgK.
Частота, где  -
-  называется частотой сопряжения.
называется частотой сопряжения.

Определим частоты сопряжения, где  (
( )
)

| 
|

| 
|

| 
|
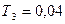
| 
|
Во что превратится  с учетом сделанных предположений:
с учетом сделанных предположений:

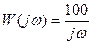 .
.





 .
.
Откладываем на оси частот частоты сопряжения.
|
|
|
Построение начинаем с интегрирующего звена: на частоте  откладываем 20lgK=20lg100=40дб и проводим линию с наклоном -20дб/дек. На частоте
откладываем 20lgK=20lg100=40дб и проводим линию с наклоном -20дб/дек. На частоте  «подсоединяем» еще одно интегрирующее звено – наклон стал -40дб/дек.
«подсоединяем» еще одно интегрирующее звено – наклон стал -40дб/дек.
На частоте  «подсоединяются» два дифференцирующих звена. У одного дифференцирующего звена наклон +20дб/дек, у двух интегрирующих звеньев наклон будет +40дб/дек, следовательно, результирующий наклон при
«подсоединяются» два дифференцирующих звена. У одного дифференцирующего звена наклон +20дб/дек, у двух интегрирующих звеньев наклон будет +40дб/дек, следовательно, результирующий наклон при  будет -40дб/дек+40дб/дек=0 дб/дек.
будет -40дб/дек+40дб/дек=0 дб/дек.
На частоте 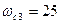 «подсоединится еще одно интегрирующее звено и наклон станет - 20 дб/дек.
«подсоединится еще одно интегрирующее звено и наклон станет - 20 дб/дек.
Фазо-частотная характеристика рассчитывается.

| 
| 
| 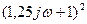 1зв 2зв
1зв 2зв
| 
| 
|

| 
|  
| 
| 
| |
| 0,2 | 
| 
|  
| 
| 
|
| 0,8 | 
| 
|  
| 
| 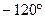
|

| 
|  
| 
| 
| |
| ∞ | 
| 
|  
| 
| 
|
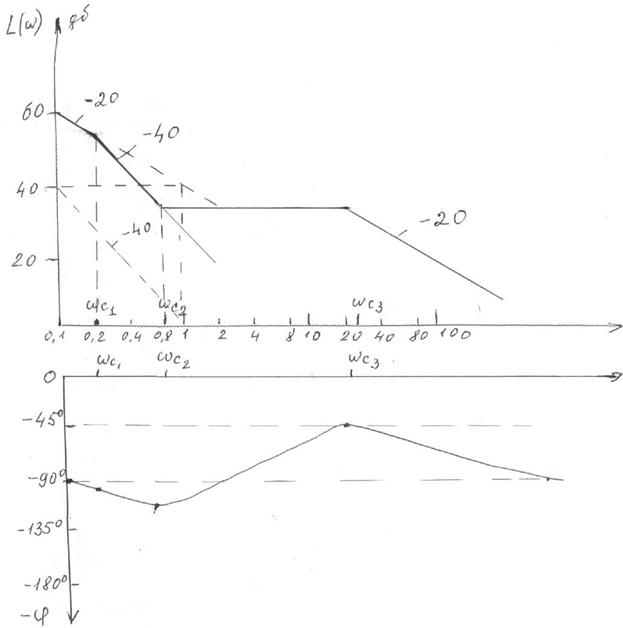
С помощью ЛАЧХ и ФЧХ нетрудно установить устойчивость замкнутой системы.
Согласно критерию устойчивости Найквиста, замкнутая САУ устойчива, если АФЧХ разомкнутой системы имеет вид (астатическая система):

|
 - запас устойчивости по фазе. Амплитуда равна 1, а до
- запас устойчивости по фазе. Амплитуда равна 1, а до 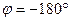 не хватает
не хватает  .
.
 - запас устойчивости по амплитуде.
- запас устойчивости по амплитуде. 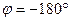 , а до равенства амплитуды 1 не хватает
, а до равенства амплитуды 1 не хватает  .
.
Теперь перенесем всё это на ЛАФЧХ.

|
На частоте 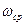 амплитуда равна 1 и поэтому
амплитуда равна 1 и поэтому  - запас устойчивости по фазе.
- запас устойчивости по фазе.
Когда фаза равна  , то
, то  - запас устойчивости по амплитуде.
- запас устойчивости по амплитуде.
Для устойчивости САУ необходимо, чтобы на 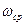

Синтез САУ с помощью ЛАЧХ
проводится следующим образом:
САУ представляют

В 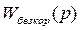 входят объект
входят объект  и известные элементы регулятора, например, измерительные, исполнительные устройства.
и известные элементы регулятора, например, измерительные, исполнительные устройства.
 - корректирующее устройство, которое надо определить в процессе синтеза.
- корректирующее устройство, которое надо определить в процессе синтеза.
Тогда передаточная функция разомкнутой системы

Здесь  - передаточная функция САУ, динамика которой удовлетворяет требованиям, предъявляемым к проектируемой системе.
- передаточная функция САУ, динамика которой удовлетворяет требованиям, предъявляемым к проектируемой системе.
Тогда в логарифмическом масштабе
 .
.
Для минимально-фазовых САУ вид ЛАЧХ полностью определяет переходный процесс и не надо рассматривать фазо-частотную характеристику.
Минимально-фазовые звенья (системы) – такие, у которых корни числителя и знаменателя расположены в левой полуплоскости. Таким образом, передаточная функция минимально-фазовой системы не должна иметь нулей и полюсов в левой полуплоскости.

|
По виду 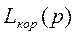 можно записать передаточную функцию корректирующего звена. В данном случае она будет иметь вид:
можно записать передаточную функцию корректирующего звена. В данном случае она будет иметь вид:
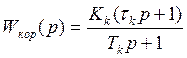 .
.
В литературе приводятся таблицы, связывающие вид  с
с
 и с соответствующими схемами корректирующих устройств, реализующих эти
и с соответствующими схемами корректирующих устройств, реализующих эти  . Приведенная выше
. Приведенная выше  может быть реализована в виде следующей корректирующей цепочки:
может быть реализована в виде следующей корректирующей цепочки:

|
Здесь 
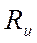 и
и  мы знаем.
мы знаем.
По графику  определяем
определяем  и
и  ,
, 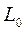 .
.
 - отсюда находим
- отсюда находим 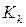 .
.
По графику  определяем
определяем 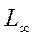 .
.

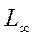 =
=  - отсюда определяем
- отсюда определяем 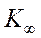 .
.
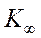 =
=  - отсюда определяем
- отсюда определяем 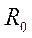 .
.
 - отсюда определяем
- отсюда определяем  .
.
 отсюда определяем
отсюда определяем 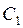 .
.
 - отсюда определяем
- отсюда определяем  .
.
Определив параметры корректирующего звена, вводим его в систему и моделируем САУ, получаем переходный процесс. Если он не устраивает – меняем параметры звена.
Требования к 
 .
.
Желаемая ЛАЧХ разомкнутой системы строится из общих требований к системе:
1. точность (определяет коэффициент усиления),
2. порядок астатизма,
3. время переходного процесса,
4. перерегулирование.

|
1.  должно пересекать ось частот в точке
должно пересекать ось частот в точке  , обеспечивающей заданное время переходного процесса
, обеспечивающей заданное время переходного процесса 
 .
.
А можно по другому:
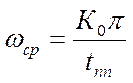 ,
, 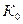 - находится из номограмм, определяющих зависимость
- находится из номограмм, определяющих зависимость  , здесь
, здесь 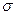 - перерегулирование.
- перерегулирование.
Например, 

2. Для того, чтобы САУ была устойчивой,  должна пересекать ось частот с наклоном - 20 дб/дек.
должна пересекать ось частот с наклоном - 20 дб/дек.
3.Для обеспечения заданного 

4.Среднечастотную часть характеристики надо делать как можно шире. Чем больше диапазон 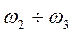 , тем ближе процесс к экспоненциальному.
, тем ближе процесс к экспоненциальному.
Среднечастотная часть в основном и определяет качество переходного процесса.
Низкочастотная часть определяет точность процесса управления.


Существует и другой способ определения конечных точек центрального отрезка:
Запас устойчивости по фазе в точке 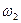 при
при  , определяемый по ЛФЧХ, должен быть не меньше
, определяемый по ЛФЧХ, должен быть не меньше 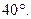
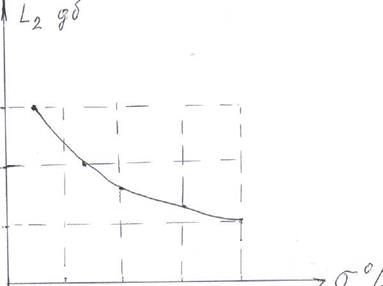
Запас устойчивости по модулю (по амплитуде) в точке L2 выбирается в зависимости от перерегулирования  :
:
|
Сопряжение центрального отрезка ЛАЧХ с низкочастотной частью производится прямой с наклоном - 40 дб/дек или – 60 дб/дек.
Высокочастотная часть, чтобы не усложнять корректирующее устройство, выбирают аналогичной исходной ЛАЧХ.
После построения  надо проверить запас устойчивости по фазе. (на
надо проверить запас устойчивости по фазе. (на 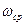
 )
)
К сожалению, этот метод синтеза не гарантирует требуемого качества переходного процесса.
Порядок расчетов при синтезе САУ с последовательным
корректирующим устройством
1. Строится ЛАЧХ неизменной части САУ (без корректирующего уст-
ройства)  .
.
2.По заданным требованиям к качеству строится желаемая ЛАЧХ  .
.
3. По  строится соответствующая ЛФЧХ.
строится соответствующая ЛФЧХ.
4. Определяются запасы устойчивости по амплитуде и фазе.
5. Путем вычитания из 
 находят ЛАЧХ корректирующего устройства
находят ЛАЧХ корректирующего устройства  .
.
6.По  выбирают его технический аналог.
выбирают его технический аналог.
7. Если технический аналог отличается, надо скорректировать  с учетом технического аналога.
с учетом технического аналога.
Если получен хороший результат, то решение задачи синтеза заканчивается. Если результат не удовлетворяет выбирается другой аналог.
Синтез САУ методом корневых годографов
Качество проектируемой САУ с точки зрения быстродействия и запаса устойчивости может характеризоваться расположением корней числителя и знаменателя передаточной функции замкнутой системы.
Зная корни, можно изобразить их расположение на комплексной плоскости. Корни могут быть определены расчетами с использованием стандартных программ.

Чем больше  - степень устойчивости, и чем меньше
- степень устойчивости, и чем меньше  - степень колебательности, тем лучше качество САУ.
- степень колебательности, тем лучше качество САУ. 
При плавном изменении значения какого-либо параметра корни будут перемещаться на плоскости корней, прочерчивая некоторую кривую, которая называется траекторией корней или корневым годографом. Построив траектории всех корней, можно выбрать такое значение варьируемых параметров, которые соответствуют наилучшему расположению корней.
Пусть имеется передаточная функция замкнутой системы
 .
.
Коэффициенты числителя и знаменателя определенным образом выражены через параметры объекта, регулятора, корректирующих устройств. Если нужно выбрать величину какого-либо параметра, то необходимо принять некоторые постоянные значения для всех остальных параметров, а для искомого параметра задавать различные числовые значения. Для каждого задаваемого значения варьируемого параметра необходимо вычислять значения корней числителя и знаменателя  и строить траектории корней, по которым выбирают то значение параметра, которое обеспечивает наилучшее расположение корней.
и строить траектории корней, по которым выбирают то значение параметра, которое обеспечивает наилучшее расположение корней.
Синтез с использованием стандартных переходных процессов
(метод стандартных коэффициентов)
Частный способ использования этого метода – диаграмма Вышнеградского для систем третьего порядка.
Стандартные переходные процессы строятся в нормированном виде при единичном входном воздействии по безразмерному времени  , где
, где 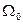 - среднегеометрический корень характеристического уравнения, определяющего быстродействие системы (не степень устойчивости).
- среднегеометрический корень характеристического уравнения, определяющего быстродействие системы (не степень устойчивости).
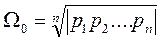 .
.
Пусть все корни вещественные и равные.
Тогда характеристическое уравнение
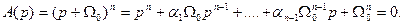 (1)
(1)
Здесь  - коэффициенты бинома Ньютона или биноминальные коэффициенты, которые определяются из треугольника Паскаля.
- коэффициенты бинома Ньютона или биноминальные коэффициенты, которые определяются из треугольника Паскаля.
Коэффициенты  имеют вид:
имеют вид:
| Порядок уравнения | Коэффициенты |
| n=1 | 1 |
| n=2 | 1,2,3 |
| n=3 | 1,3,3,1 |
| n=4 | 1,4,6,4,1 |
| n=5 | 1,5,10,10,5,1 |
Например. n=5, заданное tпп=3.По графику (ниже) находим, что  .
.
Тогда 
Тогда передаточная функция, обеспечивающая tпп=3 будет иметь вид:

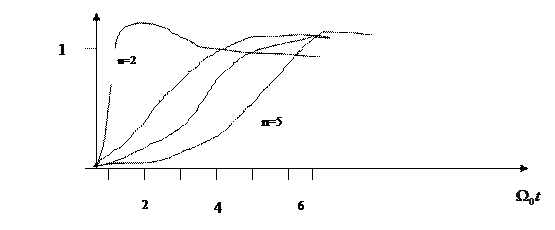
Как проводится синтез с использованием этого метода:
1. Выбирается приемлемый вид стандартного переходного процесса.
2. По нему определяется  , из которого находится
, из которого находится 
3. По 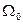 ,
,  n и коэффициентам бинома Ньютона (из таблицы) находят коэффициенты передаточной функци
n и коэффициентам бинома Ньютона (из таблицы) находят коэффициенты передаточной функци
|
|
|


