 |
Устойчивость САУ с переменными коэффициентами
|
|
|
|
В процессе работы САУ могут изменяться не только задающие и возмущающие воздействия, но и параметры самой системы.
В этом случае поведение САУ будет описываться уравнениями с переменными коэффициентами. Такие системы называются нестационарными.
Для линейных нестационарных систем диф. уравнения имеют вид:
1) для систем с одним входом и выходом (одномерные системы)

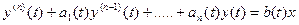 (1)
(1)
Здесь 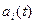 - переменные коэффициенты.
- переменные коэффициенты.
2)для систем с несколькими входами и выходами (многомерные системы)

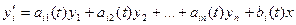 (2)
(2)
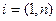 ,
, 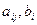 - переменные коэффициенты, зависящие от t.
- переменные коэффициенты, зависящие от t.
Такого вида уравнениями описываются, например, поведение летательного аппарата при изменении высоты и скорости полета.
На уравнения (1) и (2) без всяких изменений переносятся понятия устойчивости, рассмотренные в прошлом семестре.
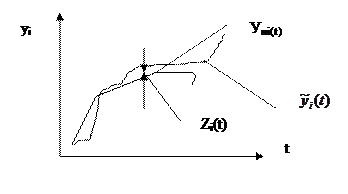
Если при любых н.у., мало отличающихся от номинальных н.у., для любого момента 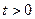 будет мала
будет мала 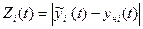 , то номинальный режим
, то номинальный режим 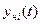 будет устойчив. Если
будет устойчив. Если  , то номинальный режим асимптотически устойчивый.
, то номинальный режим асимптотически устойчивый.
Однако практические исследования устойчивости таких систем связаны с большими трудностями, т.к. мы не всегда умеем расписывать для них решения в аналитической форме.
Для исследования САУ с переменными коэффициентами разработаны специальные методы исследования устойчивости.
Рассмотрим 2 из них.
1.Метод «замороженных» коэффициентов.
При исследовании устойчивости нестационарных систем методом «замороженных» коэффициентов системе (1) или (2) чисто формально ставится в соответствие «квазихарактеристическое» уравнение.
Для одномерной системы (1) оно будет иметь вид:
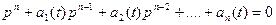 (3)
(3)
Для многомерной системы (2):
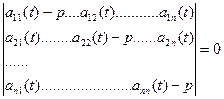 (4)
(4)
Это также уравнение 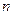 -го порядка.
-го порядка.
Пример.

Входные воздействия возьмем равными нулю.
|
|
|
Пусть динамика этой системы описывается уравнениями:
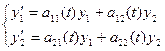
«Квазихарактеристическое» уравнение будет иметь вид:
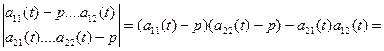


Т.к. коэффициенты этих уравнений зависят от t,то и корни характеристического уравнения также будут зависеть от времени.
Если для любого момента времени
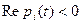 , (5)
, (5)
то в силу «замороженных» коэффициентов исходная система (1) или (2)считается устойчивой.
Однако можно показать, что существуют случаи, когда эти утверждения неверны. Существуют системы, у которых все 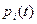 всё время находятся в левой полуплоскости, а собственные колебания системы возрастают и система неустойчива. И наоборот, есть системы, у которых один или несколько корней находятся в правой полуплоскости, а система устойчива.
всё время находятся в левой полуплоскости, а собственные колебания системы возрастают и система неустойчива. И наоборот, есть системы, у которых один или несколько корней находятся в правой полуплоскости, а система устойчива.
Можно привести дополнительные условия (Алексеев), при которых метод «замороженных» коэффициентов применим и дает надежные результаты.
Теорема
Если для системы (1) или (2) вещественные части корней 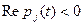 характеристического уравнения (3) или (4) при всех
характеристического уравнения (3) или (4) при всех 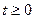 удовлетворяют условию
удовлетворяют условию
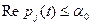 , (6)
, (6)
где  и кроме того выполняется неравенство
и кроме того выполняется неравенство
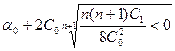 , (7)
, (7)
где 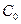 и
и  произвольные положительные константы, для которых выполняются неравенства
произвольные положительные константы, для которых выполняются неравенства
для уравнения (1) – для одномерной системы
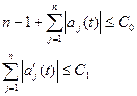 (8)
(8)
для многомерной системы (2)
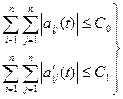 (9)
(9)
то система устойчива.
Анализ неравенства (7) показывает, что если квазихарактеристическое уравнение обладает при любом 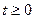 определенной степенью устойчивости (т.е самые ближние к мнимой оси корни отстоят от нее далеко) и коэффициенты
определенной степенью устойчивости (т.е самые ближние к мнимой оси корни отстоят от нее далеко) и коэффициенты 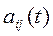 или
или  изменяются достаточно медленно, т.е.
изменяются достаточно медленно, т.е.  (производная) мала, то система будет заведомо устойчива.
(производная) мала, то система будет заведомо устойчива.
Пример. Одномерная система с переменными параметрами
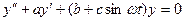
 - положительные константы.
- положительные константы.
Применим для исследования устойчивости метод «замороженных» коэффициентов.
Составим квазихарактеристическое уравнение
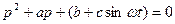
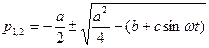
Предположим, что выражение под корнем
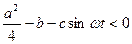 .
.
В этом случае- корни комплексно-сопряженные и их вещественная часть Re 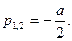
|
|
|
Таким образом за величину  в уравнении (6) можно принять
в уравнении (6) можно принять 
Определим 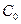 и
и  , используя (8)
, используя (8)


 (максимальное значение)
(максимальное значение)
Тогда для этого случая неравенство (7), которое гарантирует устойчивость этой нестационарной системы, примет вид
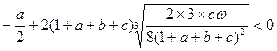 (10)
(10)
Если в это уравнение подставим заданные значения  и окажется что (10) <0, то система устойчива.
и окажется что (10) <0, то система устойчива.
Существует мнение, что наличие переменных коэффициентов усиления ухудшает свойства САУ. Однако это не всегда так. Часто некоторые коэффициенты специально заставляют изменяться по некоторому наперед заданному закону, что позволяет добиться устойчивости.
Примером таких систем могут служить системы с переменной структурой. Где коэффициент усиления замкнутой системы изменяется от 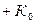 до
до 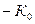 по некоторому закону.
по некоторому закону.
2. Частотный критерий устойчивости САУ с переменными коэффициентами.
Рассмотрим класс систем, у которых можно выделить переменный коэффициент  и стационарную часть.
и стационарную часть.
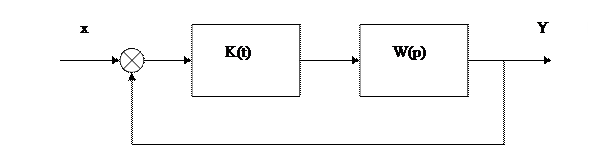
 - соответствует стационарной части системы,
- соответствует стационарной части системы, 
 - переменный коэффициент усиления, который удовлетворяет условию
- переменный коэффициент усиления, который удовлетворяет условию 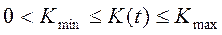 .
.
Пусть  - устойчива или нейтральна.
- устойчива или нейтральна.
Устойчива- все корни слева от мнимой оси, нейтральная- есть корень в начале координат.
Для такой замкнутой нестационарной системы справедливо следующее достаточное условие устойчивости.
Если для любого 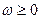 выполняется условие
выполняется условие
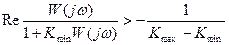 (11)
(11)
то система устойчива.
Пример.


Тогда
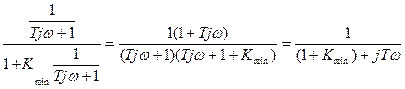 .
.
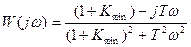
Найдем вещественную часть этого выражения.
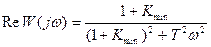

Если так, то САУ устойчива.
Если 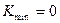 , то условие устойчивости (11) запишется
, то условие устойчивости (11) запишется
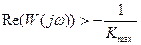
|
|
|


