 |
Элементы теории нелинейных САУ
|
|
|
|
Если при составлении математической модели САУ учитывать реально существующие эффекты, такие как трение, зазоры (люфты в механических системах), явление гистерезиса (электромагнитных цепях) нагрев элементов (джоулево тепло), различного рода ограничения, то математические модели таких систем будут описываться нелинейными дифференциальными уравнениями и статические характеристики элементов тоже будут нелинейными. Изучение таких систем связано с большими трудностями и полная теория нелинейных САУ отсутствует.
Существенные успехи в исследовании нелинейных САУ получены в тех случаях, когда удается выделить нелинейное звено и линейную часть САУ, характеризующуюся передаточной функцией. В этом случае структурную схему САУ можно представить:
Для объединения нескольких нелинейностей в одну можно использовать графический прием.
Типовые нелинейные характеристики элементов САУ:
1) Нелинейность типа зоны нечувствительности
2. Нелинейность типа ограничения
3. Нечувствительность и ограничение
4. Реле
5.Гистерезис
6.Гистерезис с зоной нечувствительности
К нелинейным системам относятся также системы, процессы в которых описываются нелинейными дифференциальными уравнениями.
Логические операции относятся также к нелинейным.
Существуют элементы, нелинейные характеристики которых не имеют кусочно-линейного характера.
Кроме того, не всегда удается выделить нелинейный элемент и линейную часть.
Мы знаем, что в линейной системе либо все номинальные режимы устойчивы, либо все – неустойчивы.
В нелинейных системах дело обстоит иначе.
Рассмотрим пример.
|
|
|
Для нелинейной системы
при 
исследовать устойчивость двух номинальных режимов
1. 
2. 
1.Приведем уравнение к стандартному виду
, но т.к. , то 
Подставляем
Вычисляем коэффициенты первого приближения
(cos 0=1)
Уравнение первого приближения
или
Т.к. 
и , то в силу критерия Гурвица система асимптотически устойчива, а следовательно и номинальный режим 
исходной системы тоже асимптотически устойчив.
2. 
Подставляем
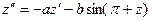
Коэффициенты
Уравнение первого приближения
или
Система неустойчива, следовательно неустойчив номинальный режим 
исходной нелинейной системы.
В линейной системе такого быть не может. У неё все режимы устойчивы или все- неустойчивы.
Приведенное уравнение описывает движение маятника и номинальный режим соответствует нижнему положению равновесия, а - верхнему.
Режимы работы САУ
| Линейные САУ | Нелинейные САУ |
| 1. Область устойчивых состояний | 1. Область устойчивых состояний (постоянное установившееся состояние) |
| 2. Область неустойчивых состояний | 2. Область устойчивых автоколебаний (колебаний с постоянной амплитудой и частотой, амплитуда и частота не зависят от начальных условий) |
| Граница устойчивости – мнимая ось | 3. Область неустойчивых состояний |
| 4. Более сложные случаи (комбинация рассмотренных выше случаев) |
В линейных системах режим работы определяется только структурой САУ и параметрами системы и не зависит от величины сигнала и начальных условий.
Режим работы нелинейной САУ зависит кроме структуры и параметров от величины входных сигналов и начальных условий.
Например, в нелинейных САУ возможны следующие режимы:
Начальные условия 
Система «в малом» неустойчива, установившееся состояние 
- неустойчиво – колебания расходятся.
Система «в большом» -начальные условия 
- устойчива
колебания сходятся. В системе возникают устойчивые автоколебания с амплитудой а.
|
|
|
2.
 | |||
 |
Система «в малом» (н.у < а) - устойчива.
Система «в большом» (н.у.> а)- устойчива.
3.
Система устойчива «в малом» (н.у < а1).
Система устойчива «в большом» (н.у.> a2).
Система неустойчива, если a1 < н.у< a2.
Для возникновения автоколебаний необходимо:
1.наличие внешнего источника энергии
2.наличие обратных связей
3.наличие нелинейного элемента.
САУ, в которых возникают автоколебания, называются автоколебательными системами. В некоторых САУ – автоколебания полезны (генераторы в радиотехнике, вибрационные регуляторы, мультивибраторы). В некоторых САУ – это нежелательное явление.
Устойчивость номинальных режимов в замкнутой одноконтурной системе с нелинейным элементом
Рассмотрим САУ, структурная схема которой может приведена к виду:
Рис.1
В этой системе передаточная функция линейной части
Тогда уравнения элементов, входящих в состав этой системы, имеют вид:
(1)
(2)
(3)
Здесь в уравнении (1) N(y) и M(u) – линейные дифференциальные операторы, соответствующие членам N(p) и M(p) передаточной функции линейной части.
Если, например, 
,
то 
, 
.
Таким образом, запись (1) – это обозначение дифференциального уравнения (1), соответствующего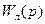 
.
Предположим, что в нелинейной системе (рис.1) существует номинальный режим, характеризуемый функциями 
Ограничимся изучением случая, когда 
и 
не зависят от времени, т.е. = 
, = 
.
Из определения номинального режима следует
Положим
Подставим эти выражения в (1), (2), (3).
Получим, используя свойства линейных дифференциальных операторов
Вычитая из соотношений , , соответственно уравнения , , , получаем
.
Разложив функцию 
в ряд Тейлора по степеням 
и объединяя члены, содержащие в степени больше 1, в остаток, имеем
Отбросим остаток 
, вычтем 
и обозначим 
. (4)
Тогда получим
.
Таким образом, мы получили систему уравнений первого приближения
(5)
(6)
(7)
Линейной системе уравнений (5,6,7) соответствует структурная схема линейной САУ
Рис.2
Эта структурная схема называется структурной схемой линеаризованной системы, соответствующей номинальному режиму 
исходной нелинейной САУ. 
|
|
|
Рис.3
Геометрически процедура получения коэффициента Кн по формуле (4) состоит в определении тангенса угла наклона касательной к нелинейной характеристике 
в рабочей точке 
. Эта процедура называется линеаризацией нелинейной характеристики.
Теорема Ляпунова
Если система первого приближения (5,6,7) (или что тоже структурная схема рис.2) асимптотически устойчива, то будет асимптотически устойчив и номинальный режим в исходной нелинейной системе (1,2,3) (структурная схема рис.1)
Если система (5,6,7) неустойчива, то будет неустойчив и номинальный режим в нелинейной САУ.
Пример. Для структурной схемы рис.1, где
исследовать устойчивость номинального режима
, 
Запишем уравнения системы
Поскольку 
То можно применять описанный выше метод.
Найдем по (4) коэффициент 
линеаризованной характеристики
, а 
, то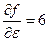 
Структурная схема будет иметь вид:
Исследуем САУ на устойчивость.
Найдем 
= 
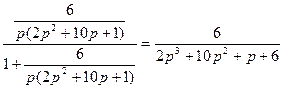
Характеристическое уравнение
По критерию устойчивости Гурвица – система неустойчива. Если неустойчива система первого приближения, значит, неустойчив и номинальный режим в исходной нелинейной системе.
В этой системе можно указать другой номинальный режим, который будет асимптотически устойчив. Для этого надо рабочую точку сдвинуть влево в область достаточно малых 
Устойчивость в целом
До сих пор при изучении номинальных режимов мы ограничивались рассмотрением устойчивости по Ляпунову, которая является,по существу, устойчивостью «в малом», т.е. изучалось поведение САУ при малых начальных отклонениях от номинального режима.
Будем говорить, что номинальный режим НЛ САУ устойчив в целом, если он устойчив по Ляпунову и при любых «отклоненных» начальных условиях 
(см. определение устойчивости) выполняется соотношение 
Второй метод Ляпунова
Рассмотрим предложенный А.М.Ляпуновым способ исследования устойчивости в целом в замкнутой САУ.
Рассмотрим многомерную систему, характеризуемую величинами
Пусть в этой многомерной системе существует номинальный режим
|
|
|
,
Обозначим разность «отклоненного» и номинального режимов через
(1)
Второй метод Ляпунова заключается в следующем:
Если удается найти такую функцию 
, которая
1. положительна при всех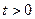 
и 
,
2. производные от этих функций отрицательны, т.е.
при всех 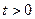и при всех 
(за исключением точек 
, где они могут обращаться в ноль)
то решение устойчиво в целом.
Пример. Исследовать устойчивость в целом системы
Все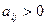 
Рассмотрим функцию 
.
удовлетворяет условия (1), т.к. все .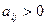
Вычислим 
Условие (2) тоже выполнено и система устойчива в целом.
К сожалению, нет общего приема построения функции Ляпунова .
Однако для ряда конкретных САУ они найдены и приведены в литературе (Постников, Лурье…..)
Замечание. Если не удалось найти функцию , это не означает, что САУ неустойчива, возможно эту функцию удастся найти.
Абсолютная устойчивость
Рассмотрим структурную схему НЛ САУ, в которой можно выделить НЭ и линейную часть.
Рис.1
На практике вид нелинейной характеристики не всегда бывает известен с достаточной точностью. Часто бывает известна лишь область (сектор), в которой эта нелинейная характеристика может находиться. Эта область задается неравенством
(1)
Номинальный режим в замкнутой НЛ САУ (рис.1) называется абсолютно устойчивым, если он устойчив в целом при любой нелинейной характеристике , удовлетворяющей условию (1).
Далее будем рассматривать НЛ САУ, которая работает в режиме стабилизации, т.е.
, (2)
т.е. номинальный режим – состояние покоя.
|
|
|
