Методы расчета уширенных пролетных строений

1. Методика расчета уширенных железобетонных пролетных строений с использованием программ PRNY и RSTV

Основные положения расчета

Расчет уширенных пролетных строений производят в соответствии с требованиями стандартов СЭВ 384-76, 1406-78, норм проектирования СНиП 2.05.03-84, а также специальных требований, вытекающих из специфики работы уширенных пролетных строений.

Расчет в предельном состоянии состоит в проверке условия

S _пр> S ^*, (1)

где S _пр - предельное усилие (момент, поперечная сила), соответствующее достижению рассматриваемой группы предельных состояний; S ^* - усилие от действия расчетной нагрузки.

Предельное усилие должно определяться на основе требований СНиП 2.05.03-84.

При определении S _пр в элементах уширенных пролетных строений, в которых объединены ранее эксплуатировавшиеся и новые материалы, следует учитывать состояние самонапряжения и ограниченную деформативность материалов, а также дефекты в ранее эксплуатировавшейся конструкции.

Определение усилий от нагрузки в общем случае производят в форме:

S ^*= f_s (g, l ₀, П), (2)

где f_s - функциональная зависимость, связывающая параметры; g - интенсивность нагрузки; l ₀ - пролет рассматриваемого элемента, в качестве которого принимают минимальное расстояние между точками опирания в направлении рабочего армирования; П - группа параметров, определяющих пространственную работу конструкции.

Допускается наряду с формулой (2) использовать зависимость

S ^*=S P_i g _i w _i h _i, (3)

где Р_i - интенсивность нормативных нагрузок; g _i - коэффициент надежности по нагрузке; w _i - функционал, связывающий усилие и пролет l ₀, рассматриваемого элемента; h _i - коэффициент, учитывающий пространственную работу конструкции (определяют по таблицам или на основе расчетов).

Расчеты по настоящему приложению производят при проектировании уширения разрезных балочных пролетных строений. В исследовательских целях, а также для анализа напряженно-деформированного состояния пролетных строений в линейной постановке допускается использовать программы, основанные на методе конечных элементов и методе плитно-балочной конструкции.

Расчет комбинированных нормальных сечений в предельных состояниях

Расчет сечений с дефектами, в которых объединены в совместную работу материалы, имеющие различный возраст, допускается производить с использованием действительных диаграмм деформирования с применением п.п.п. SEPGU и SEPMY, которые разработаны на кафедре мостов МАДИ для расчета нормальных сечений железобетонных элементов.

Сечение представляется как совокупность зон (рис. 1), имеющих форму четырехугольника для бетона и принимаемых в виде точек с сосредоточенной в них площадью для арматуры. Зоны группируют исходя из единства материала и времени включения в совместную работу. По каждой группе зон должны быть заданы:

диаграмма деформирования материала, которую принимают по системе нормируемых показателей (если известен класс (марка) материала или путем испытания образцов с учетом коэффициента надежности по материалу;

параметры эпюры относительных деформаций, соответствующей моменту включения группы зон в работу всего сечения.

Расчет производят путем решения методами нелинейного математического программирования системы уравнений равновесия сечения:

(4)

где n - число групп зон в сечении.

Рис 1 Расчетная схема и основная система для расчета линий влияния М, g, Н, HK

В результате расчета определяют: значение предельного изгибающего момента М _пр, соответствующее достижению e_пр в одном из материалов, составляющих сечение при условии:

;

параметры напряженно-деформированного состояния, отвечающие условию (4), если М _пр³ М ^*.

П.п.п. SEPGU дает возможность рассчитывать сечения, имеющие не более двух групп зон, моделирующих бетон. При использовании п.п.п, SEPMY число групп зон не ограничено (в практике расчетов встречаются сечения с четырьмя группами зон).

П.п.п. SEPGU и SEPMY имеются в распоряжении ВЦ ГипродорНИИ и МАДИ.

Расчет уширенных пролетных строений с дефектами при учете физической нелинейности

Определение усилий и перемещений в уширенных пролетных строениях с дефектами рекомендуется производить с использованием пространственной расчетной схемы в виде перекрестной системы стержневых элементов, имеющих нелинейную связь между усилиями и деформациями (рис. 2). Анализ такой расчетной схемы допускается производить с помощью п.п.п. ROSTV, которая имеется в распоряжении ВЦ ГипродорНИИ и МАДИ.

Стержни первого уровня моделируют работу главных балок, элементы второго уровня - работу поперечной конструкция (плиты, диафрагмы). На стержне размещается сетка сечении; по каждому из них устанавливается диаграмма изгиба. Она учитывает наличие дефектов, влияющих на геометрию стержня (выколы, трещины, коррозия арматуры) и связанных с изменением свойств материалов (выщелачивание, карбонизация бетона).

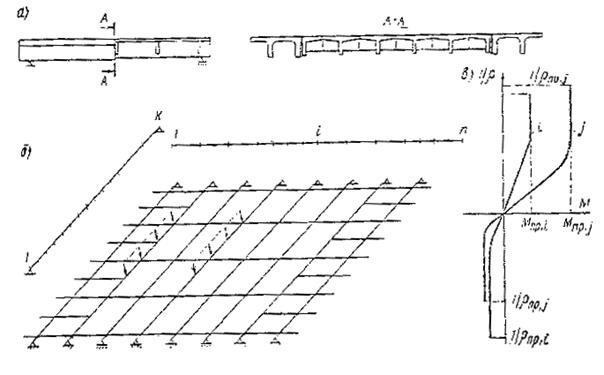
Рис. 2. Исходная информация для расчета пролетного строения (а), стержневая пространственная расчетная схема (б) и диаграммы изгиба сечений стержневых элементов (в)

Решение задачи определения усилий и перемещений производят на основе метода сил с привлечением аппарата нелинейного математического программирования для решения нелинейной системы совместности перемещений.

В качестве исходных данных вводят: информацию о геометрии системы (координаты начала и конца стержней, точек пересечения, положения сечений); данные о работе сечений (диаграммы изгиба); данные о нагрузке.

В результате расчета по программе ROSTV устанавливают эпюры усилий и перемещений в системе, которые фиксируют в назначенных сечениях.

Расчет уширенных железобетонных пролетных строений по программе PRNY

Для определения величин h _i может быть использована общая постановка метода коэффициента поперечной установки.

На. основе этого метода составлена программа PRNY, в которой исходная информация и принятые допущения обозначены следующим образом:

А - в поперечном сечении располагают балки с различными геометрическими характеристиками в общем случае (рис. 3).

Б - распределение усилий между балками (плитами) происходит только в том поперечном сечении, где приложено внешнее сосредоточенное усилие. Это означает, что балки (плиты) пролетного строения как бы разделены продольными швами, оставляя соединенными только участки на рабочей ширине в рассматриваемом поперечном сечении с внешним усилием. Внешние усилия в поперечных сечениях распределяются независимо друг от друга.

В - для каждой балки выделяют участок шириной А. Внутри этих участков балки работают на кручение как жесткие брусья без деформации их контура.

Г - по бокам жесткой части назначают зоны АК^лев и АК^прав, характеризующие изгибаемые в поперечном направлении части сечения каждой балки.

Д - поперечное сечение пролетного строения характеризуется параметрами, задаваемыми для каждой балки:

момент инерции на кручение РК;

модуль упругости материала К;

модуль сдвига материала G.

Рис. 3. Исходная информация для расчета нормального сечения:

а - сечение моделируется тремя группами зон; б - эпюра деформаций до объединения в совместную работу; в - эпюры деформаций и напряжений в предельном состоянии; г, д - диаграммы деформирования бетона и арматуры

Е - поперечная жесткость конструкции для каждой балки характеризуется моментом инерции на изгиб PR в продольном сечении пролетного строения на рабочей ширине B _р.

Ж - влияние длины и опорных закреплений каждой из балок, объединяемых в единое пролетное строение, учитывается показателями В и ВВ. В - прогиб одной i -й балки при действии на нее единичной вертикальной силы, приложенной в рассматриваемом сечении, увеличенной в expr раз. ВВ - угол закручивания i -й балки от крутящего момента, равного, приложенного к ней в рассматриваемом сечении, увеличенного в GХPK _i раз.

Результатами расчета являются значения следующих параметров для каждого положения груза Р= 1:

m ₁, М ₂,..., М - изгибающие моменты в проведенных сечениях;

Q ₁, Q ₂... - поперечные силы в тех же сечениях;

H ₁, H ₂,..., H - вертикальные давления, передающиеся на балки с учетом всех воздействий;

НК ₁, НК ₂,..., НК - крутящие моменты, передающиеся на балки с учетом всех воздействий.

Если введен признак расчета 1-3 или 1-4, то на печать выводятся значения изгибающих моментов и поперечных сил между всеми балками при очередном положении единичного груза, ординаты линий влияния давлений на последовательные балки, ординаты линий влияния закручивающих моментов на последовательные балки.

Если введен признак 1-1 или 1-2, то на печать выводятся только ординаты линий влияния давлений и закручивающих моментов на последовательные балки.

Копию программы PRNY можно заказать с подлинников в ВЦ Минавтодора РСФСР, МАДИ и ГипродорНИИ.

П.п.п. PSTV рекомендуется для расчета балочных ребристых пролетных строений уширенных мостов, реконструируемая часть которых имеет локальные дефекты (коррозию арматуры, выщелачивание бетона, разрушение стыков сборных элементов). PSTV может быть использован как при линейном расчете конструкции, так и при необходимости учета физической нелинейности.

П.п.п. PRNY рекомендуется для определения усилий в уширенных приставными элементами пролетных строений, при проектировании PRNY не предусматривает учета зональных дефектов и нелинейности деформирования железобетона в предельном состоянии.

2. Основные положения расчета сталежелезобетонного пролетного строения с использованием программы

2.1. Программа SK, написанная на алгоритмическом языке «Фортран-IV», позволяет производить расчет разрезных сталежелезобетонных двухбалочных пролетных строений на стесненное кручение от временной нагрузки с учетом переменности сечения по длине.

В основе алгоритма решении лежит теория В.З. Власова совместно с некоторыми положениями численного анализа.

Неоднородное дифференциальное уравнение равновесия с переменными коэффициентами имеет вид:

;

после подстановки

,

y'' -r(x) y = f (x). (5)

Данное уравнение решаем относительно депланации y, используя для этого метод прогонки. Перегоночные коэффициенты имеют вид (прямой ход):

C_n =1/(2+r² _nh ²- C_n -1)

j _n = C_n (j _{n -1}- f_nh ²). (6)

Решение получаем в виде линейной комбинации (обратный ход):

Y_{n -1}= C_{n -1} Y_n +j _{n -1}. (7)

Из граничных условий имеем:

C ₀=1, j₀=0, Y_N = y_{N -1}

Зная размер депланации в N +1 точках значения усилий и напряжений получаем, пользуясь дифференциальными зависимостями:

M _кр= Gl_d q'; t_кр= G q'd;

B _w=- EI _wq''; s_w=- E q''w; (8)

M _w=- EI _wq'''; t_w=- E q''' S _w^отс/d;

Для аппроксимации функции угла закручивания q воспользуемся формулой численного дифференцирования:

. (9)

При этом полученную систему линейных уравнений решаем также методом прогонки. Прогоночные коэффициенты вычисляют по формулам (прямой ход):

C_{n -1}=1/(4-3 C_{n -2}); (10)

j _{n -1}= C_{n -1}(3j _{n -2}+2 hY_{n -2}).

Значения угла закручивания получаем аналогично (7) (обратный ход):

q _{n -1}= C_{n -1}q _n +j _{n -1}.

Граничные условия представлены в виде:

C ₀=0₁, j₀=0, q _{N -1}=j _{N -1}.

2.2. Область применения программы ограничивается следующими возможностями:

расстояние между главными балками не должно быть более ¹/₄ расчетного пролета;

количество мест изменения сечения на половине пролета не более 10;

количество одновременно рассчитываемых сечений не более 20 на половине пролета.

2.3. Ввод исходных данных осуществляется в соответствии с бланками, изображенными на рис. 4, 5, 6.

Вывод информации производится в виде таблиц. При этом имеется пять вариантов печати - один основной и четыре дополнительных. Для назначения того или иного варианта служит индекс управления печатью IP, вводимый с исходными данными (см. рис. 6).

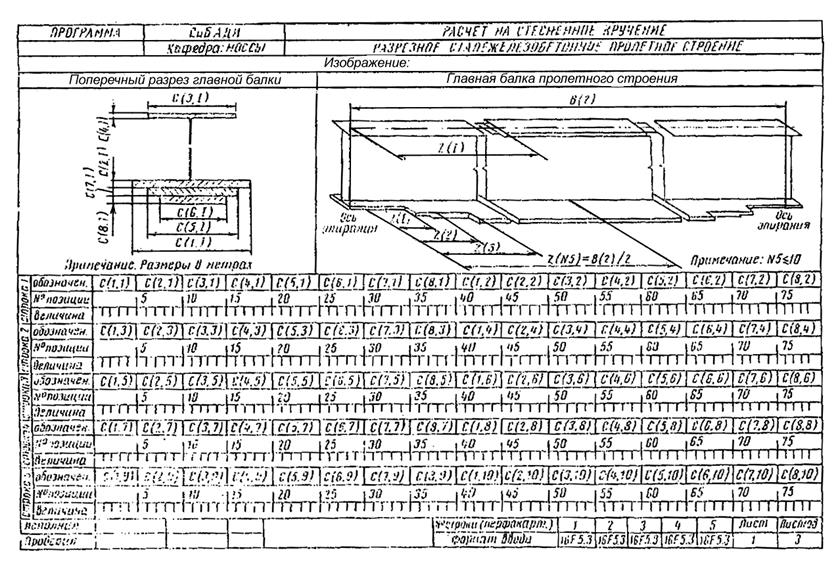
Рис. 4

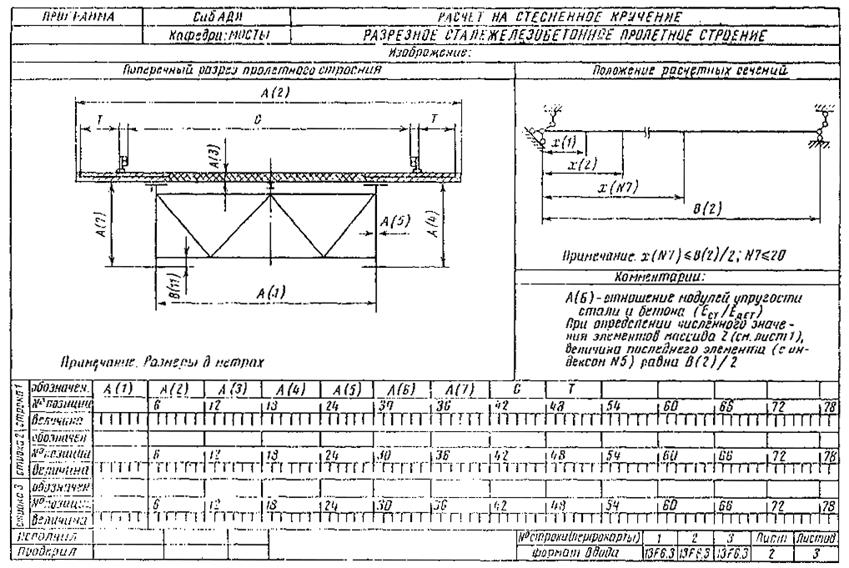
Рис. 5

Рис. 6

Таблица 1. Варианты вывода информации

Значение IP	Наименование варианта	Дополнительные сведения о выданной информации
	Основной	1. Геометрические характеристики сечений
2. Силовые факторы стесненного кручения
3. Нормальные напряжения
4. Касательные напряжения
	Дополнительный	1. Геометрические характеристики сечений
	»	2. Силовые факторы
	»	3. Нормальные напряжения
	»	4. Касательные напряжения

Возможные варианты вывода информации в зависимости от индекса управления печатью IP приведены в табл. 1.

Использование основного варианта позволяет получать для каждого сечения максимальный объем информации в виде таблиц. Пример информации для сечения х =21 м показан в табл. 2-5.

Использование дополнительного варианта дает возможность выводить информацию частями (пример показан в табл. 6-8).

Таблица 1. Геометрические характеристики сечения

Момент инерции секториальный, м6	Момент инерции крученая, м4	Положение ц. т. от низа вертикала, м	Расстояние от ц. т. плиты до центра изгиба, м
3,30316	0,0754	2,058	0,852

Таблица 3. Силовые факторы от временной нагрузки

Общий крутящий момент, т·м (кН·м)	Крутящий момент, т·м (кН·м)	Биомомент, т·м2 (кН·м2)	Изгибно-крутящий момент, т·м (кН·м)
-1,51 (-15,1)	-0,06 (-0,6)	-109,72 (-1097,2)	-1,46 (-14,6)
-14,84 (-148,4)	-0,55 (-5,5)	-1076,35 (-10763,5)	-14,29 (-142,9)

Таблица 4. Нормальные напряжения от кручения временной нагрузкой

В нижнем поясе, кг/см2 (МПа)	В верхнем поясе, кг/см2 (МПа)	На уровне ц. т. плиты, кг/см2 (МПа)
24,1 (2,4)	-7,5 (-0,7)	-2,0 (-2,0)
Угол закручивания: Ф =-0,1510569 Е -02 рад.

Таблица 5. Касательные напряжения от кручения временной нагрузкой

На уровне ц. т., кг/см2 (МПа)	Максимальные в стенке, кг/см2 (МПа)	На верхней грани плиты, кг/см2 (МПа)
0,8 (0,1)	0,8 (0,1)	0,8 (0,1)

Таблица 6. Геометрические характеристики сечения

Момент инерции секториальный, м6	Момент инерции крученая, м4	Положение ц. т. от низа вертикала, м	Расстояние от ц. т. плиты до центра изгиба, м
х =1,000 м
1,88593	0,07539	2,289	0,569
х= 2,000 м
1,88593	0,07539	2,289	0,569
х= 4,200 м
1,88593	0,07539	2,289	0,569
х =8,400 м
2,84132	0,07540	2,133	0,763
х =12,600 м
3,30316	0,07541	2,058	0,852
х =18,800 м
3,30316	0,07541	2,058	0,852
х =21,000 м
3,30316	0,07541	2,058	0,852

2.4. При использовании для решения задачи ЭВМ СМ-4 необходимый объем памяти без оптимизации расположения массивов находится в интервале от 40 до 56 Кбайт. Время счета около 10 с.

Копию программы SK можно заказать с подлинников, которые находятся в ВЦ Минавтодора РСФСР и СибАДИ.

Таблица 7. Силовые факторы от временной нагрузки

Общий крутящий момент, т·м (кН·м)	Крутящий момент, т·м (кН·м)	Биомомент, т·м2 (кН·м2)	Изгибно-крутящий момент, т·м (кН·м)
х =1,000 м
-24,35	-14,11	-9,64	-10,22
-238,84	-138,41	-94,58	-100,27
х= 2,000 м
-23,20	-14,12	-18,87	-9,08
-227,64	-138,56	-185,12	-89,09
х= 4,200 м
-19,12	-13,60	-34,88	-5,52
-187,61	-133,39	-342,16	-54,15
х =8,400 м
-14,33	-11,09	-76,86	-3,24
-140,57	-108,81	-754,020	-31,81
х =12,600 м
-11,10	-7,75	-102,05	-3,36
-108,92	-76,00	-1001,09	-32,93
х =18,800 м
-2,46	-2,10	-109,35	-0,36
-24,09	-20,63	-1072,71	-3,49
х =21,000 м
-1,51	-0,06	-109,72	-1,46
-14,84	-0,55	-1076,35	-14,29

Таблица 8. Нормальные напряжения от кручения временной нагрузкой

В нижнем поясе, кг/см2 (МПа)	В верхнем поясе, кг/см2 (МПа)	На уровне ц. т. плиты, кг/см2 (МПа)
х =1,000 м
3,8 0,4	-0,7 -0,1	-0,2 -0,0
Угол закручивания: Ф =-0,8926201 Е -04 рад
х= 2,000 м
7,5 0,7	-1,3 -0,1	-0,4 -0,0
Угол закручивания: Ф =-0,1932385 Е -03 рад
х= 4,200 м
13,9 1,4	-2,4 -0,2	-0,7 -0,1
Угол закручивания: Ф =-0,4489926 Е -03 рад
	х =8,400 м
19,4 1,9	-5,3 -0,5	-1,5 -0,1
Угол закручивания: Ф =-0,9113585 Е -03 рад
х =12,600 м
22,4 2,2	-6,9 -0,7	-1,9 -0,2
Угол закручивания: Ф =-0,1264877 Е -02 рад
х =18,800 м
24,0 2,4	-7,4 -0,7	2,0 -0,2
Угол закручивания: Ф =-0,1501302 Е -02 рад
х =21,000 м
24,1 2,4	-7,5 -0,7	-2,0 -0,2
Угол закручивания: Ф =-0,1510569 Е -02 рад

3. Методика определения прогибов и усилий в элементах уширенных пролетных строений по программе ЭМ-10 ХАДИ

Теоретической основой программы является энергетический метод, переработанный для разрезных пролетных строений из разного материала с диафрагмами и без них. Программа составлена на языке PL для реализация на ЭВМ ЕС.

Методика позволяет быстро определять прогибы и усилия в конструкциях с любым количеством балок. Для экономии машинного времени и ввода меньшего количества исходных данных в программе ЭМ-10 ХАДИ предусмотрено наибольшее количество балок - 15 шт., что достаточно для расчета большинства реальных мостов. Время работы ЭВМ зависит от формы обращения к ЭВМ: если программа вводится с помощью перфокарт - время работы ЭВМ от 1 до 5 мин; если программа записана в памяти ЭВМ - до 1 мин.

При первой схеме загружения ЭВМ устанавливает линейную полосовую нагрузку 1 т/м (100 Н/см) над первой балкой и далее автоматически переставляет нагрузку над всеми остальными балками. В результате счета ЭВМ печатает данные (прогибы и изгибающие моменты в середине пролета; поперечные силы на опоре; изгибающие моменты в продольных сечениях плиты или диафрагме), которые используются как эпюры влияния прогибов или усилий.

Загружение эпюр влияния с помощью ЭВМ не предусмотрено, так как машина, очень долго анализирует результаты расчетов при определении наихудшего условия (в большинстве случаев имеется не один, а несколько максимумов).

Эпюры влияния следует вычертить на миллиметровой бумаге и в худшем положении установить нагрузку. Худшим считают такое положение, при котором произведение нагрузки q _экв на сумму ординат-эпюр влияния под нагрузкой будет наибольшим.

Так как эквивалентную нагрузку вычисляют по изгибающему моменту и в программе используется ограниченное количество членов ряда, значения прогибов получаются с некоторым завышением (наибольшее равно 25% при одной сосредоточенной силе в середине пролета), при испытаниях мостов с малым количеством машин на пролете (2-4 шт.) теоретические прогибы желательно вычислять с поправкой.

Для проверки правильности расчетов при вычислении изгибающих моментов в главных балках может быть использовано условие:

;

или

å M_i= å P_iy_i ±(5%¸10%),

где å M_i - сумма значений изгибающих моментов во всех главных балках при одинаковом расположении нагрузки над всеми эпюрами; или å P_iy_i - изгибающий момент от рассматриваемой линейной или полосовой нагрузки при загружении простой балки.

Исходные данные для программы ЭМ-10 ХАДИ: количество балок (блоков), расчетный пролет, расстояния между балками и от края плиты (накладные тротуары не учитываются), моменты инерции при изгибе и кручении балок, модули упругости и коэффициенты Пуассона материала плиты и ребер. В программе заложено, что плита выполнена из одного материала (единое значение коэффициента Пуассона), а ребра могут быть из разнородных материалов.

Ниже приведен пример определения прогибов и усилий в элементах пролетного строения, построенного по типовому проекту вып. 56 СДП, уширенного блоками по типовому проекту 710/5 и усиленного путем укладки монолитной железобетонной плиты толщиной 10 см над старой частью пролета. Схема пролетного строения приведена на рис. 7, а. Пролетное строение рассчитывали в двух вариантах: с передачей М и Q в поперечном направлении только на диафрагмы и с передачей всего усилия поперек моста на новую монолитную плиту. Второй вариант дал более благоприятный результат, так как армирование диафрагм оказалось недостаточным.

Исходные данные второго варианта: l _p=1110 см; n =10 шт.; D ₁= D ₁₁=85 см; D ₂= D ₁₀=166 см; D ₃= D ₉=40 см; D ₄= D ₅= D ₆= D ₇= D ₈=140 см; I ₁= I ₁₀=3370000 см⁴; I ₂= I ₉=2866000 см⁴; I ₃= I ₈=2910000 см⁴; I ₆= I ₇=3559000 см⁴; I _кр1= I _кр10=357000 см⁴; I _кр2= I _кр9=312000 см⁴; I _кр3= I _кр8=460000 см⁴; I _кр4= I _кр5= I _кр6= I _кр9=823000 см⁴; Коэффициент Пуассона плиты g=0,167; I _пл10=29400 см⁴; I _пл2,9=29400 см⁴; I _пл3= I _пл4=…= I _пл2=131200 см⁴; E _пл1= E _пл2= E _пл3=…= E _пл11=315000 кг/см² (31500 МПа); E _р1= E _р2=…= E _р10=315000 кг/см² (31500 МПа); v_р1=v_р2=…=v_р10=0,167

В табл. 9 приведены значения ординат эпюр влияния прогибов и усилий, вычисленные на ЭВМ. На рис. 8 приведена эпюра, результаты загружения которых приведены в табл. 10 и 11.

Выводы по приведенному примеру (табл. 5-6):

а) изгибающий момент в l /2 средних балок не превышает допустимого для этих конструкций;

б) объединение конструкций по плите h =10 см и сохранение верхних накладок в существующих конструкциях обеспечивает нормальное распределение усилий между балками;

в) монолитная плита должна армироваться в двух уровнях с площадью нижней арматуры на 1 м Fa =18 см² (девять стержней Æ 16 П).

Рис. 7. Эпюры прогибов и изгибающих моментов в l /2 главных балок

Таблица 9. Значение ординат эпюр влияния прогибов и усилий

Схема загружения	№ балки	Прогибы W, см	Изгибающие моменты в l /2 главной балке М, кН·м	Поперечные силы на эпюре Q, кH	Изгибающие моменты в плите М пл, кН·м
		0,039	3,27	9,42	0,074
	0,044	1,53	8,92	0,332
	0,044	1,95	9,04	1,650
	0,038	4,28	9,70	1,578
	0,026	23,28	6,59	0,597
	0,011	9,94	2,81	0,740
	-0,001	0,47	0,13	1,694
	-0,005	-3,43	-0,97	-1,722
	-0,004	-3,15	-0,89	-0,345
	0,002	1,68	0,48	0,076
		0,007	6,07	1,72	0,144
	0,034	24,35	6,89	0,546
	0,038	28,04	7,93	2,767
	0,045	40,67	11,51	3,014
	0,039	35,07	9,92	1,901
	0,024	21.84	6,18	0,110
	0,009	8,04	2,28	-1,373
	-0,001	-0,38	-0,11	-1,752
	-0,001	-0,38	-0,11	-1,752
	-0,002	-1,30	-0,37	-0,086

Таблица 10. W ₄, М ₄, Q ₄ от нагрузки НК-80 q _экв/2=56,5 кН/м

№ балки	q экв	Приборы	Изгибающие моменты	Поперечные силы
	y 1	y 2	å yi	W, см	y 1	y 2	å yi	М, (кН·м)	y 1	y 2	å yi	Q, кН
	5,65	0,039	0,039	0,078	0,44	3,25	3,20	6,45	364,0	0,95	0,93	1,86	105,0

Рис. 8. Эпюры влияния поперечных сил в главных балках на опоре (а) и изгибающих моментов (б) в плите (в l /2 пролетного строения)

Таблица 11. Вычисление изгибающих моментов в продольных сечениях плиты в l /2 пролетного строения

№ сечения	q экв	y 1	y 2	å yi	М пл, кН·м/м
кН/м
	5,65	-0,01	-0,17	-0,18	-1,02
		-0,25	0,23	0,48	+2,71

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: