 |
Принцип относительности Эйнштейна.
|
|
|
|
Принцип Галилея подразумевает, что время течет во всех инерциальных системах отсчета одинаково, то есть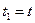 
. На самом деле есть убедительные сомнения в справедливости такого утверждения. Дело в том, что по представлениям Галилея взаимодействия (любого типа) между материальными точками происходит мгновенно. Однако более поздние исследования, например, электромагнитные взаимодействия между быстро движущимися частицами запаздывают. Частица успевает сместиться, а сила, действующая на неё, остается прежней. Начало подобным исследованиям и сомнениям было положено изучением скорости света. Оказалось, что скорость света в вакууме – предельная скорость. Говорят, что во всех инерциальных системах скорость света постоянна. Это инвариантность скорости света. Учет этого экспериментального обстоятельства с принципом относительности составил новый для классической физики спе циальный принцип относительности Эйнштейна.
Выяснилось, что инвариантом при скоростях, близких к скорости света являются так называемые интервалы. Эйнштейну пришлось перейти от рассмотрения трехмерного геометрического мира к четырехмерному пространственно-временному миру. В этом мире (он вполне реален и является обобщением привычного трехмерного мира) «расстояние» между близкими пространственно-временными точками (интервал) равен
.
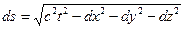Физическая ценность интервала между двумя событиями состоит в том, что он инвариантен (постоянен) в любых инерциальных системах отсчета. Это свойство является математическим выражением постоянства скорости света (в вакууме).
Релятивистские формулы, приводящие к инвариантности интервала, называются преобразованиями Лоренца. Они указывают, как перейти от координат инерциальной системы отсчета (включая время), которая движется со скоростью v вдоль положительного направления оси х.
|
|
|
Преобразования имеют вид (
– скорость света в вакууме),
,
Указанные преобразования симметричны:
.
При малых скоростях, когда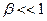 
Преобразования Лоренца переходят в преобразования Галилея. Таким образом, классическая механика является частным случаем релятивистской механики для малых скоростей.
Заметим, что ограничение скорости перемещения материальных тел скоростью света (в вакууме) имеет более общий характер. Скорость света считается максимальной скоростью перемещения не только вещества, но и энергии, а значит – скорости передачи информации.
Заметим еще, что при больших скоростях масса материальной точки начинает зависеть от скорости, релятивистское выражение для массы приобретает вид
,
где 
– носит название «масса покоя». Изменение массы покоя при изменении скорости отражает фундаментальный факт связи массы и энергии частицы.
Гармонический осциллятор.
Рассмотрим простую физическую систему – материальную точку, которая без трения колеблется на горизонтальной поверхности под действием
силы Гука (см. рис. 2).
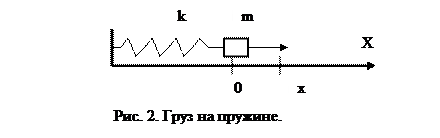
Если смещение груза много меньше, чем длина недеформированной пружины, а жесткость пружины равна k, то но груз действует единственная сила, сила Гука. Тогда уравнение движения груза (Второй закон Ньютона) имеет вид
Перенеся слагаемые в левую часть равенства, и разделив на массу материальной точки m (массой пружины пренебрегаем по сравнению с m), получим уравнение движения
(*),
где
и
есть циклическая частота и период колебаний.
Тогда, взяв функцию
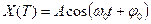
и продифференцировав её по времени, убеждаемся, что скорость движения груза равна
,
а после повторного дифференцирования ускорение
,
то есть X(t) действительно является решением уравнения груза на пружинке.
|
|
|
Рассмотренная система, вообще любая система, механическая, электрическая или иная, обладающая уравнением движения (*), называется гармоническим осциллятором. Функция типа X(t) носит название закона движения гармонического осциллятора; величины 
называются амплитудой, циклической или собственной частотой, начальной фазой гармонического осциллятора. Частота определяется параметрами осциллятора, амплитуда и начальная фаза задаются начальными условиями.
Закон движения X(t) представляет собой свободные колебания. Такие колебания совершают незатухающие маятники (математический или физический), ток и напряжения в идеальном колебательном контуре и некоторые другие системы.
Гармонические колебания могут складываться в одном, или в различных направлениях. Результатом сложения тоже оказывается гармоническое колебание, например,
.
Это принцип суперпозиции (наложения) колебаний.
Математики разработали теорию рядов такого рода, которые называются рядами Фурье. Имеется также ряд обобщений типа интегралов Фурье (частоты могут меняться непрерывным образом) и даже интегралы Лапласа, работающие с комплексными частотами.
|
|
|
