Состояние термодинамического ансамбля. Уравнения состояния.

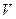Говоря о материальной точке, мы отмечали, что её механическое состояние определяется шестью функциями времени: . В термодинамических и статистических ансамблях тоже используется понятие состояния. Это так называемые макроскопические (т.е. характеризующие всю систему или значительную её часть) параметры. В простейшем случае это объем системы , давление и её термодинамическая или абсолютная температура . В системе СИ давление измеряется в паскалях . Нормальное давление составляет . Как дополнительный параметр часто указывают энтропию S, которую мы определим позже. В некоторых случаях указывают энтальпию, а также свободную энергию.

Если удается для какой-то термодинамической модели установить соотношение

,

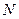( – число частиц в ансамбле), то говорят, что задано уравнение состояния системы.

Единого уравнения состояния не существует. Укажем две модели, лежащие в основе термодинамики.

Модель идеального газа.

Идеальным считается газ из материальных точек, не взаимодействующих друг с другом. Это разреженные одноатомные и молекулярные газы или их смеси. Уравнение состояния такого ансамбля можно вывести из основных постулатов динамики материальной точки. Оно получило названия «Уравнение состояния идеального газа» или «Уравнение Менделеева – Клайперона»:

или, что то же самое, .

Здесь 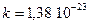Дж/К – постоянная Больцмана, Дж/(моль К),

– число молей газа, 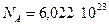1/моль – число частиц в одном моле или число Авогадро.

Модель газа Ван-дер-Ваальса.

В отличие от идеального газа, модель Ван-дер-Ваальса лучше соответствует реальным газам. Она учитывает рассеяние частиц друг на друге (то есть молекулярные силы) или внутреннее давление , а также собственный объем моля частиц . Внутреннее давление можно выразить формулой

,

где – константа для данного газа.

Если газ содержит молей, то уравнение состояния Ван-дер-Ваальса имеет вид

.

Поправки к уравнению идеального газа должны быть много меньше параметров .

Указанные примеры относятся к однородным системам, в которых нет переноса массы, импульса и энергии (отсутствие потоков массы, импульса и энергии является условием термодинамического равновесия).

Термодинамическое равновесие – очень интересное состояние системы. Не надо думать, что там нет потоков энергии, импульса и вещества. Потоки есть, но они одинаковы по всем направлениям, то есть компенсируют друга. Это динамическое равновесие.

Возникновение динамического равновесия является следствием очень давней гипотезы о молекулярном хаосе, согласно которой все направления в пространстве равноправны для термодинамической системы (система изотропна). Отталкиваясь от идеи молекулярного хаоса после небольших преобразований можно получить важное соотношение, связывающее температуру ансамбля со средней энергией, приходящейся на одну частицу (атом или материальную точку; для молекул картина несколько сложнее):

.

Указанное равенство считается определением термодинамической или абсолютной температуры. Из него следует возможность определения средней скорости частиц:

, .

Вектор средней скорости, по гипотезе о молекулярном хаосе, равен нулю.

В статистической физике средние значения энергии и скорости получают без гипотезы о молекулярном хаосе на основе статистических распределений.

Если термодинамическое равновесие нарушено и в ансамбле возникли потоки, то говорят, что возникают процессы переноса вещества (диффузия), энергии (теплоперенос, теплопроводность), импульса (внутреннее трение или вязкость). Возможны и другие процессы переноса, в частности, возникновение электрического тока.