 |
Коэффициент износа и годности основных фондов на конец года 2 глава
|
|
|
|
Относительный показатель интенсивности (ОПИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:
.
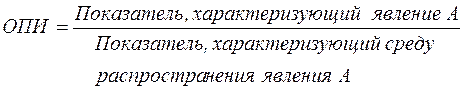Данный показатель получают сопоставлением разноименных, но взаимосвязанных в своем развитии величин. Поэтому наиболее часто он представляет собой именованную величину, но может быть выражен в процентах, промилле.
Например, для определения уровня обеспеченности населения легковыми автомобилями рассчитывается число автомашин, приходящихся на 100 семей, для определения плотности населения рассчитывается число людей, приходящихся на 1 км².
Разновидностью относительных показателей интенсивности являются относительные показатели уровня экономического развития, характеризующие производство продукции расчете на душу населения и играющие важную роль в оценке развития экономики государства. Так как объемные показатели производства по своей природе являются интервальными, а показатель численности населения – моментным, в расчете используют среднюю за период численность населения (например, среднегодовую).
Пример 2.5
Рассматривая лишь абсолютный размер ВВП России в 1 квартале 1996 г. (508 трлн руб.), трудно оценить, или «почувствовать», эту величину. Для того чтобы на основе данной цифры сделать вывод об уровне развития экономики, необходимо сопоставить ее со среднеквартальной численностью населения страны (148,1 млн чел.), которая в простейшем случае рассчитывается как полусумма численности населения на начало и на конец квартала. В результате размер ВВП на душу населения составит 3,43 млн руб.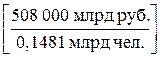 
.
Относительный показатель сравнения (ОПС) представляет собой соотношение одного и того же абсолютного показателя, характеризующего разные объекты (предприятия, фирмы, районы, области, страны и т.п.):
|
|
|
.
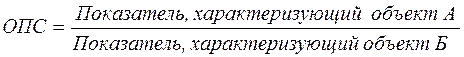Пример 2.6
На начало 1996 г. операции с ГКО – ОФЗ проводили в Москве 108, в Новосибирске 16 и в Санкт-Петербурге 13 официальных дилеров. Таким образом, в Москве дилеров было в 6,8 раза больше, чем в Новосибирске 
, и в 8,3 раза больше, чем в Санкт-Петербурге 
.
2.2. Задачи для самостоятельного решения
Задача 2.1
За отчетный период предприятие произвело следующие виды мыла и моющих средств:
| Виды мыла и моющих средств | Количество, кг |
| Мыло хозяйственное 60%-ной жирности | |
| Мыло хозяйственное 40%-ной жирности | |
| Мыло туалетное 80%-ной жирности | |
| Стиральный порошок 10%-ной жирности |
Определить общее количество выработанной продукции в условно-натуральных единицах измерения. За условную единицу измерения принять мыло 40%-ной жирности.
Задача 2.2
Имеются следующие данные о розничном товарообороте Российской Федерации за 1996-1997 гг., млрд руб.:
| Показатель | 1996 г. | 1997 г. |
| Общий объем розничного товарооборота в том числе: продовольственные товары непродовольственные товары | 753,3 361,9 391,4 | 862,6 420,7 441,9 |
Исчислите относительные величины структуры розничного товарооборота. Дайте сравнительный анализ изменения структуры.
Задача 2.3
Имеются данные о ценах на спортивные детские товары за отчетный период, руб. за единицу:
| Вид товара | Отечественное производство | Зарубежное производство |
| Костюм спортивный Футболка Куртка спортивная | 91,0 13,1 141,7 | 160,4 19,5 156,2 |
Определите относительные показатели сравнения цен по каждому виду товара.
Задача 2.4
Численность населения в Российской Федерации на 1 января 1997 г. составила 147,5 млн человек, в том числе: городского – 107, 8 млн человек; сельского – 39,7 млн человек.
Исчислите долю городского и сельского населения в общей численности населения Российской Федерации.
|
|
|
Сравните численность городского и сельского населения страны.
Задача 2.5
В апреле 1996 г. прожиточный минимум в РФ для трудоспособного населения составил 419,0 тыс. руб. в месяц на человека, для пенсионеров – 262, 5 тыс. руб., для детей – 376,1 тыс. руб. Сделайте выводы о соотношении этих величин, используя относительные показатели сравнения.
3. Средние величины
3.1. Методические указания
и решение типовых задач
Средняя является обобщающей характеристикой совокупности единиц по качественно однородному признаку.
В статистике применяются различные виды средних: арифметическая, гармоническая, квадратическая, геометрическая и структурные средние – мода и медиана. Средние, кроме моды и медианы, исчисляются в двух формах: простой и взвешенной.
Важнейшее свойство средней заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Это объясняется тем, что в средней взаимно поглощаются те отклонения индивидуальных значений признака, которые обусловлены действием случайных факторов.
Таким образом, средняя отражает типичный уровень признака и абстрагируется от индивидуальных особенностей, присущих отдельным единицам.
Определить среднюю во многих случаях удобнее через исходное соотношение средней (ИСС) или ее логическую формулу:
.
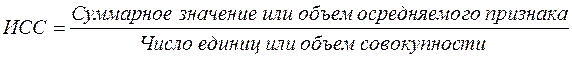Пример 3.1
По данным табл. 3.1 рассчитать:
1) среднюю численность персонала по трем предприятиям;
2) средний фонд заработной платы по данным граф 1 и 2;
3) средний фонд заработной платы по данным граф 1 и 3;
4) средний фонд заработной платы, если известны данные только по графам 2 и 3.
Таблица 3.1
Заработная плата предприятий АО
| Предприятие | Численность промышленно-производственного персонала, чел. (ППП) | Месячный фонд заработной платы, тыс. руб. | Средняя заработная плата, руб. |
| А | |||
| 564,84 331,54 517,54 | |||
| Итого | 1413,92 | ? |
Решение
1. Среднюю численность персонала определим по формуле простой средней арифметической:
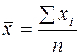, (3.1)
где n – объем совокупности;
xі – численность персонала на каждом предприятии.
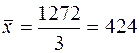чел.
Для определения средней заработной платы вычислим исходное соотношение средней. Независимо от имеющихся в нашем распоряжении данных средняя заработная плата может быть получена только через следующее отношение:
|
|
|
.
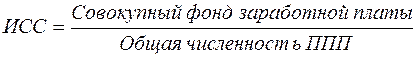2. Предположим, что мы располагаем только данными гр. 1 и 2 табл. 3.1. Итоги этих граф содержат необходимые величины для расчета искомой средней. Воспользуемся формулой средней агрегатной:
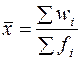; (3.2)
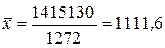руб.,
где w i = xi fi;
xi – i -тый вариант осредняемого признака;
f i – вес i -того варианта.
3. Если мы располагаем только данными о средней заработной плате и численности работников (гр. 1 и 3), то нам известен знаменатель исходного соотношения, но не известен его числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на числитель ППП. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
; (3.3)
руб.
Допустим теперь, что в нашем распоряжении только данные о фонде заработной платы и средней заработной плате персонала (гр. 2 и 3 табл. 3.1), т.е. нам известен числитель исходного соотношения, но не известен его знаменатель. Численность работников по каждому предприятию можно получить делением фонда заработной платы на среднюю заработную плату. Тогда расчет средней заработной платы в целом по трем предприятиям будет произведен по формуле средней гармонической взвешенной:
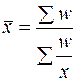; (3.4)
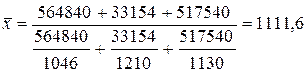руб.
В подобных случаях при равенстве весов (W) расчет среднего показателя может быть произведен по средней гармонической невзвешенной:
.
Пример 3.2
Рассмотрим табл. 3.2. Определим величину среднедушевого денежного дохода в целом по Российской Федерации. Исходное соотношение такой средней будет иметь следующий вид:
.
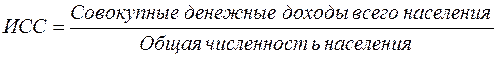Таблица 3.2
Распределение населения РФ в IV квартале 1996 г.
по уровню среднедушевых денежных доходов
| Среднедушевой денежный доход в среднем за месяц, тыс. руб. | Численность населения, % к итогу |
| До 400 400 – 600 600 – 800 800 – 1000 1000 – 1200 1200 – 1600 1600 – 2000 2000 и выше | 30,2 24,4 16,7 10,5 6,5 6,7 2,7 2,3 |
| Итого |
Перейдем от интервалов к их серединам. При этом величину первого интервала условно приравняем к величине второго, тогда его нижняя граница будет равна 200 тыс. руб. Величину последнего интервала условно приравняем к величине предпоследнего, тогда его верхняя граница составит 2400 руб. В результате получаем следующие середины интервалов:
|
|
|
300 500 700 900 1100 1400 1800 2200.
Роль численности населения в данном случае выполняет его доля в общем итоге, выраженная в процентах. Для расчета воспользуемся средней арифметической взвешенной (3.3):
тыс. руб.
Следовательно, среднедушевой денежный доход в целом по Российской Федерации составлял 688,5 тыс. руб.
Наряду с рассмотренными степенными средними статистика использует для анализа вариационных рядов и структурные средние – моду и медиану.
Мода (М 0) определяет собой значение изучаемого признака, повторяющееся с наибольшей частотой.
Медиана (Ме) – значение признака, которое делит ранжированный ряд пополам. Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:
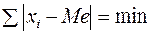. (3.5)
Для определения медианного значения признака находят номер медианной единицы ряда (NMe) по следующей формуле:
NMe = 
, (3.6)
где n – объем совокупности.
Если получаем дробное значение (например 6,5), то это значит, что медиана лежит между 6 и 7 номерами значения признака.
Пример 3.3
В бригаде из 9 человек рабочие имеют следующие тарифные
разряды:
4 3 4 5 3 3 6 2 6
Для определения медианы надо провести ранжирование:
2 3 3 3 4 4 5 6 6
Центральным в этом ряду является рабочий 4 разряда. Это и будет медиана.
Так как в бригаде больше всего рабочих 3 разряда, этот тарифный разряд будет модальным.
Если мода отражает типичный, наиболее распространенный вариант значения признака, то медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальному закону распределения совокупности. Проиллюстрируем ее познавательное значение следующим примером.
Пример 3.4
Необходимо дать характеристику среднего дохода группы людей, насчитывающей сто человек, из которых 99 имеют доходы в интервале от 100 до 200 долл. в месяц, а месячные доходы последнего составляют 50000 долл. (табл. 3.3).
Таблица 3.3
Месячные доходы исследуемой группы людей
| № п/п | … | … | ||||||||
| Доход, долл. | … | … |
Если мы воспользуемся средней арифметической, то получим средний доход, равный примерно 700 долл., который не только в несколько раз меньше дохода 100-го человека, но и имеет мало общего с доходами остальной части группы. Медиана же, равная в данном случае 163 долл., позволит дать объективную характеристику уровня доходов 99% данной группы людей.
Рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения).
|
|
|
Пример 3.5
Предположим, распределение рабочих всего предприятия по тарифному разряду имеет следующий вид (табл. 3.4).
Таблица 3.4
Распределение рабочих предприятия по тарифному разряду
| Тарифный разряд | Численность рабочих, человек |
| Всего |
Определение моды по дискретному вариационному ряду не составляет большого труда – наибольшую частоту (60 человек) имеет 5-й тарифный разряд, следовательно, он и является модальным.
Расчет медианы дает значение
.
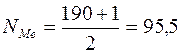Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 95-м и 96-м рабочими. Необходимо определить, к какой группе относятся рабочие с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Очевидно, что рабочих с этими номерами нет в первой группе, где всего лишь 12 человек, нет их и во второй группе (12+48=60). 95-й и 96-й рабочие находятся в третьей группе (12+48+56=116), следовательно, медианным является 4-й тарифный разряд.
Для интервальных рядов определение моды и медианы проводится по следующим формулам:
(3.7)
где хо – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
i – величина модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
(3.8)
где хо – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
i – величина медианного интервала;
SMe-1 – накопленная частота интервала, предшествующего медианному;
fMe – частота медианного интервала.
Пример 3.6
Определить моду и медиану по исходным данным, представленным в табл. 3.5.
Таблица 3.5
Распределение торговых предприятий города
по размеру среднесуточного товарооборота
| Среднесуточный товарооборот, млн руб. | Число предприятий | Накопленная частота (расчетная) |
| до 10 | ||
| 10 – 20 | ||
| 20 – 30 | ||
| 30 – 40 | ||
| 40 – 50 | ||
| 50 – 60 | ||
| 60 и более | ||
| ИТОГО | - |
Решение
Используем формулы (3.8) и (3.9):
млн руб.;
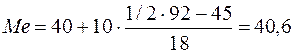млн руб.
Пример 3.7
Вдоль шоссе расположены 5 магазинов. Магазины находятся на втором, пятом, десятом, двадцать пятом и шестидесятом километрах. Обработка статистических данных показала, что в среднем за период будут обращаться на базу: первый магазин – 5 раз, второй – 10 раз, третий – 15 раз, четвертый – 10 раз, пятый – 40 раз. Требуется решить вопрос о таком местонахождении базы снабжения, при котором сумма пробегов от магазинов до базы была бы минимальной.
Решение
По свойству медианы (3.6) сумма пробегов будет минимальной, если база снабжения расположится в точке медианы ряда.
Ряд строится так, что расположение магазинов принимается за значение признака, а число ездок – за частоту.
| xi (км) | |||||
| mi |
Сумма ездок равняется 80.
Номер медианы определяем по (3.7):
,
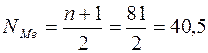где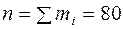 
.
Следовательно, медиана находится между 40 и 41 значениями ряда.
Значение медианы:
; 
км.
Таким образом, сумма пробега будет минимальной, если база снабжения будет построена на 42,5 км шоссе.
Пример 3.8
Требуется определить среднемесячную заработную плату одного рабочего по следующим данным (графы 1 и 2 нижеприведенной таблицы).
| Месячная зарплата, руб. | Число рабочих, f i | Середина интервала, xi | fj xi | Накопленные частоты S |
| 2400 – 2500 | ||||
| 2500 – 2600 | ||||
| 2600 – 2700 | ||||
| 2700 – 2800 | ||||
| 2800 – 2900 | ||||
| 2900 – 3000 | ||||
| Итого | - | - |
По формуле средней арифметической взвешенной (3.3) зарплата одного рабочего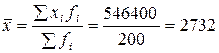 
руб.
Наибольшую частоту (60) имеет интервал 2700 – 2800.
Моду определяем по формуле (3.8):
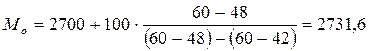руб.
Наиболее часто встречается зарплата в размере 2731,6 руб.
Для определения медианы вычислим её номер в ряду.
Порядковый номер медианы
.
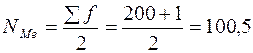Сотая единица находится в интервале (2700 – 2800).
Медиану определим по формуле (3.9):
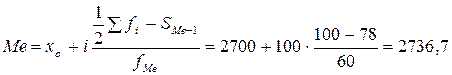руб.,
т.е. половина рабочих получают зарплату ниже 2736,7 руб., а половина – выше.
Мода и медиана могут быть определены и графически: первая – по гистограмме, вторая – по кумуляте.
Рассмотрим гистограмму распределения (рис. 3.1), для чего на оси абсцисс построим ряд сомкнутых прямоугольников, у каждого из которых основанием служит величина интервала признака (размер заработной платы в рублях), а высотой – частота каждого интервала (число рабочих). (Для рядов с неравными интервалами в качестве высоты прямоугольников принимается плотность распределения.)
В прямоугольнике, имеющем наибольшую высоту, проводим две линии, как показано на рис. 3.1, и из точки их пересечения опускаем перпендикуляр на ось абсцисс. Значение х на оси абсцисс в этой точке есть мода (М 0).
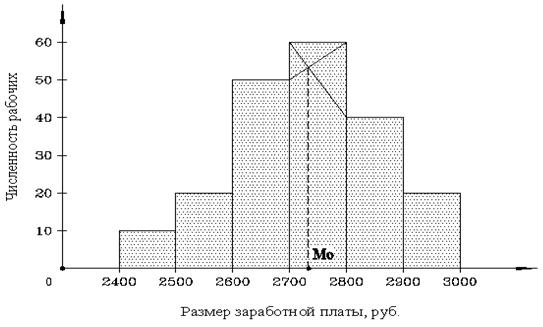
Р и с. 3.1. Гистограмма распределения 200 рабочих по размеру
заработной платы (графическое определение моды)
Для графического отыскания медианы по накопленным частотам строим кумуляту (рис. 3.2). Для этого из верхней границы каждого интервала на оси абсцисс восстанавливаем перпендикуляр, соответствующий по высоте накопленной частоте с начала ряда по данный интервал. Соединив последовательно вершины перпендикуляров, мы и получим кривую, называемую кумулятой. Из точки на оси ординат, соответствующей половине всех частот (порядковому номеру медианы), проводим прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Опустив из этой точки перпендикуляр на ось абсцисс, находим значение медианы (Ме).
Пользуясь кумулятой, можно определить значение признака у любой единицы ранжированного ряда.
Аналогично рассчитываются показатели, именуемые квартилями. Первая квартиль (Q1) – значение признака у единицы, делящей ранжированный ряд в соотношении¼ и ¾, вторая квартиль равна медиане (Q2 = Ме), третья квартиль(Q3) – значение признака у единицы, делящей ранжированный ряд в соотношении¾и ¼. Порядковый номер Q1 определяется как Σ f/ 4, для Q3 – соответственно как ¾ Σ f.
Р и с. 3.2. Кумулята распределения 200 рабочих по размеру заработной платы (графическое определение медианы)
Представляет интерес и расчет показателей, именуемых децилями (значение признака у единицы, делящей ранжированный ряд в соотношении 1 / 10 и 9 / 10 (первая дециль – D1), 2 / 10 и 8 / 10 (вторая дециль – D2) и т.д.
Для симметричных распределений характерно совпадение значений средней арифметической, моды и медианы. Если М0 >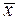 
, то ряд будет иметь левостороннюю асимметрию (вытянутость), а если М0 < 
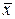, то правостороннюю асимметрию. В умеренно асимметричных рядах соотношение между указанными показателями выражается следующим образом:
| М 0 – 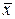| ≤ 3 | Ме – |.
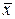3.2. Задачи для самостоятельного решения
Задача 3.1
Доходы пяти банков по операциям с ценными бумагами за отчетный период составили: 0,4; 0,7; 0,8; 1,1; 1,2 (ден. единиц).
Определить средний доход банка по данной операции.
Задача 3.2
Имеются данные страховых организаций области о числе заключенных договоров по личному добровольному страхованию.
| № группы | Число договоров, тыс. | Число страховых организаций | Удельный вес страховых организаций, % | Число заключенных договоров |
| I II III IV V | ||||
| Итого |
Определить среднее число заключенных договоров в расчете на одну страховую организацию области.
Задача 3.3
По данным выборочного наблюдения имеется следующее распределение фермерских хозяйств района по размерам угодий.
| № группы | Хозяйства по размерам угодий, га | Число хозяйств | Середина интервала |
| I II III IV V | До 40 40-50 50-60 60-70 Свыше 70 | ||
| Итого | — |
Определить средний размер угодья на одно фермерское хозяйство по району.
Задача 3.4
Имеются следующие данные о показателях работы предприятий отрасли за отчетный период.
| Показатель | № предприятия | ||||
| Объем продукции, тыс. шт. Стоимость реализ. продук., тыс.руб. Прибыль, тыс. руб. | 9,0 | 9,8 | 8,5 | 8,6 | 9,1 |
Определите средние уровни каждого показателя по предприятиям отрасли.
Задача 3.5
Имеются следующие данные о продаже картофеля на рынках
города.
| № рынка | Средняя цена, руб. | Продано, тыс. кг. | Удельный вес продажи, % | ||
| Март | Май | Март | Май | ||
| 3,5 3,0 2,5 |
Определите средние цены картофеля по трем рынкам города в марте и мае, используя в качестве частот:
а) абсолютные данные о продаже товара,
б) удельные веса продажи товара.
Объясните, почему при неизменных ценах и общем объеме продажи средняя цена в мае изменилась.
Задача 3.6
Имеются группы предприятий по темпам сокращения промышленного производства:
| Сокращение производства, % | До 15 | 15-25 | 25-35 | 35-45 | Свыше 45 |
| Число предприятий |
Определите средний процент сокращения промышленного производства по совокупности предприятий.
Задача 3.7
За отчетный период имеются следующие данные по пяти малым предприятиям отрасли.
| Показатель | № предприятия | ||||
| Среднесписочная численность работников, чел. Средняя заработная плата, руб. |
Определите среднюю заработную плату работников предприятий отрасли.
Задача 3.8
Распределение предприятий региона по размеру прибыли характеризуется следующими данными.
| Балансовая прибыль, млн руб. | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | Свыше 60 |
| Удельный вес предприятий, % |
Определите среднюю прибыль предприятия.
Задача 3.9
Имеются данные о финансовых показателях фирм, тыс. руб.
| № фирмы | Получено прибыли | Акционерный капитал | Рентабельность акционерного капитала, % | Удельный вес акционерного капитала, % |
| А | ||||
Определите средний процент рентабельности акционерного капитала фирм, используя показатели: а) гр. 1 и 2; б) гр. 2 и 3; в) гр. 1 и 3; г) гр. 3 и 4.
|
|
|
