Коэффициент износа и годности основных фондов на конец года 3 глава

Задача 3.10

Имеются следующие данные об оплате труда работников малых предприятий.

№ пред- приятия	Фонд заработной платы, руб.	Среднесписочная численность работников, чел.	Среднемесячная заработная плата, руб.	Удельный вес работников, %
А
	270 000 240 000

 

Определите среднюю заработную плату работников предприятия, используя показатели: а) гр. 1 и 2; б) гр. 2 и 3; в) гр. 1 и 3; г) гр. 3 и 4.

Задача 3.11

По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города.

Размер вклада, руб.	До 400	400-600	600-800	800-1000	Свыше 1000
Число вкладчиков

 

Определите:

1) средний размер вклада;

2) дисперсию, среднее квадратическое отклонение и коэффициент вариации вкладов.

Задача 3.12

Имеются следующие выборочные данные о расходах на платные услуги домохозяйствами района.

 

Домохозяйства	Обследовано домохозяйств	Доля расходов на платные услуги, %
Городских поселений Сельской местности

 

Определите для домохозяйств района:

1) общую дисперсию;

2) среднюю из групповых дисперсий;

3) межгрупповую, используя правило сложения дисперсий.

Поясните полученные показатели.

4. Показатели вариации

4.1. Методические указания
и решение типовых задач

Для измерения степени изменяемости отдельных значений признака от средней исчисляются основные обобщающие показатели вариации.

Размах вариации является наиболее простым измерителем вариации признака и определяется как разность между наибольшим и наименьшим значениями признака:

R = x_max – x_min. (4.1)

 

Среднее линейное отклонение представляет собой среднюю величину из отклонений вариантов признака от средней, учитывая различия всех единиц совокупности:

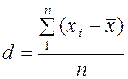простое (для дискретного ряда значений признака); (4.2)

взвешанное (для интервального ряда). (4.3)

Дисперсия – это средний квадрат отклонений, определяемый как средняя из отклонений, возведенных в квадрат.

простая (для дискретного ряда); (4.4)

взвешенная (для интервального ряда). (4.5)

Среднее квадратическое отклонение

. (4.6)

Коэффициент вариации – относительное среднее квадратическое отклонение, определяющее изменяемость признака:

(4.7)

Если 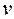> 40%, это говорит о большой изменяемости признака.

Здесь:

x_max – максимальное значение признака;

x_min – минимальное значение признака;

n – число вариантов в дискретном ряду;

m – число интервалов в интервальном ряду;

x_i – i -тое значение варьирующего признака (вариант);

x_j – значение варьирующего признака в середине j -того интервала;

f_j – частота.

По величине коэффициента вариации можно судить о степени вариации признаков, а следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу.

Пример 4.1

Имеются выборочные данные о стаже работников коммерческих банков (табл. 4.1).

Таблица 4.1

Стаж, лет	Среднесписочная численность работников, чел. f	Середина интервала xi	xif
До 3				-3
3 – 5				-1
5 – 7
7 – 9
Свыше 9
Итого		-		-	-

 

Определить:

1) средний стаж работников;

2) дисперсию;

3) среднее квадратическое отклонение;

4) коэффициент вариации.

Решение

1. Средний стаж работников рассчитывается по формуле (3.1):

тыс. руб.

2. Дисперсия определяется по формуле (4.6):

.

3. Среднее квадратическое отклонение составит величину

.

4. Коэффициент вариации вычисляется по формуле (4.7):

.

Статистическую совокупность можно считать однородной по рассматриваемому признаку, если коэффициент вариации не превышает 33% [1].

Статистическое изучение вариации многих социально-экономических явлений проводится и при помощи дисперсии альтернативного признака. Обозначим наличие данного признака 1, отсутствие – 0, долю вариантов, обладающих данным признаком, – p, а не обладающих им– q.

Дисперсия альтернативного признака 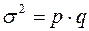, (4.8)

где

; (4.9)

n – число наблюдений;

m – число единиц совокупности, обладающее данным признаком.

q = 1 – p (4.10)

Пример 4.2

Определим дисперсию альтернативного признака по следующим данным: налоговой инспекцией одного из районов города проверено 172 коммерческих киоска и в 146 обнаружены финансовые нарушения. Тогда п = 172, т = 146; ; q = 1 – 0,85 = 0,15;

.

Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.

Если данные представлены в виде аналитической группировки, то можно вычислить дисперсию общую, межгрупповую и внутригрупповую.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:

. (4.11)

Межгрупповая дисперсия () характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле

(4.12)

где и n_i – соответственно групповые средние и численности по отдельным группам.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:

(4.13)

Средняя из внутригрупповых дисперсий :

. (4.14)

Существует закон, связывающий три вида дисперсии. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсии:

. (4.15)

Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу, общая дисперсия, возникающая под действием всех факторов, равна сумме дисперсии, появляющейся под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.

Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.

Пример 4.3

Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным табл. 4.2.

Таблица 4.2

Производительность труда двух бригад рабочих-токарей

 

1-я бригада	2-я бригада
№ п/п	Изготовлено деталей за час, шт. xi	xi – x 1	(xi – x 1)2	№ п/п	Изготовлено деталей за час, шт. xi	xi – x 1	(xi – x 1)2
		-2 -1				-3 -2 -1

 

Решение

Для расчета групповых дисперсий вычислим средние по каждой группе:

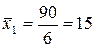шт.; шт.

Промежуточные расчеты дисперсий по группам представлены в табл. 4.2. Подставив полученные значения в формулу (4.4), получим

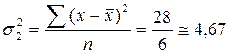
Средняя из групповых дисперсий

.

Затем рассчитаем межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних:

шт.

Теперь определим межгрупповую дисперсию:

.

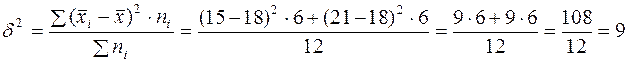Таким образом, общая дисперсия по правилу сложения дисперсий составит величину

.

Проверим полученный результат, исчислив общую дисперсию обычным способом:

.

На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результативным признаками. Он называется эмпирическим корреляционным отношением, обозначается («эта») и рассчитывается по формуле

. (4.16)

Для нашего примера эмпирическое корреляционное отношение .

Величина 0,86 характеризует существенную связь между группировочным и результативным признаками.

Величина называется коэффициентом детерминации и показывает долю межгрупповой дисперсии в общей дисперсии.

Наряду с вариацией количественных признаков может наблюдаться и вариация качественных признаков. Такое изучение вариации достигается, как и для долей количественных признаков, посредством вычисления и анализа следующих видов дисперсий.

Внутригрупповая дисперсия доли определяется по формуле

. (4.17)

Средняя из внутригрупповых дисперсий рассчитывается так:

. (4.18)

Формула межгрупповой дисперсии имеет следующий вид:

, (4.19)

где n_i – численность единиц в отдельных группах;

– доля изучаемого признака во всей совокупности, которая определяется по формуле

. (4.20)

Общая дисперсия имеет вид

. (4.21)

Три вида дисперсии связаны между собой следующим образом:

. (4.22)

Пример 4.4

Определим групповые дисперсии, среднюю из групповых, межгрупповую и общую дисперсии по данным табл. 4.3.

Таблица 4.3

Численность и удельный вес одной из категорий
крупного рогатого скота фермерских хозяйств района

Хозяйство	Удельный вес дойных коров, % pi	Всего коров ni
Итого

Решение

Определим долю дойных коров в целом по трем хозяйствам:

;

.

Общая дисперсия доли дойных коров

.

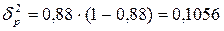Внутригрупповые дисперсии:

; ; .

Средняя из внутригрупповых дисперсий:

.

Межгрупповая дисперсия:

.

Используя правило сложения дисперсий, получаем: 0,1025 +
+ 0,0031 = 0,1056. Пример решен правильно.

Пример 4.5

По данным выборочного обследования заработной платы работников бюджетной сферы получены следующие показатели.

 

Отрасль	Средняя заработная плата, руб. xi	Численность работников, чел. fj	Дисперсия заработной платы σ i2
Здравоохранение
Образование

 

Определить:

1) среднюю заработную плату по двум отраслям;

2) дисперсии заработной платы:

а) среднюю из групповых дисперсий (отраслевых),

б) межгрупповую (межотраслевую),

в) общую;

3) коэффициент детерминации и эмпирическое корреляционное отношение.

Решение

1. Средняя заработная плата работников по двум отраслям по формуле (3.3) равна величине

руб.

2. а) средняя из групповых дисперсий согласно (4.14)

;

б) межгрупповая дисперсия по формуле (4.12)

в) применяя правила сложения дисперсий, получим общую дисперсию (4.15):

.

3. а) Коэффициент детерминации

, (4.23)

, или 44,24%.

Он показывает, что оплата труда на 44,24% зависит от отраслевой принадлежности работников и на 55,76% – от внутриотраслевых
причин;

б) по формуле (4.16) эмпирическое корреляционное отношение составляет

,

что свидетельствует о существенном влиянии на дифференциацию заработной платы отраслевых особенностей.

4.2. Задачи для самостоятельного решения

Задача 4.1

Имеются следующие данные по распределению 60 рабочих по тарифному разряду.

Тарифный разряд (x)
Число рабочих (f)

Определить:

1) средний тарифный разряд рабочих;

2) среднее линейное отклонение;

3) дисперсию;

4) среднее квадратическое отклонение;

5) коэффициент вариации.

Задача 4.2

По результатам экзаменационной сессии 1 и 2 курсов одного из вузов имеются следующие данные: на 1 курсе 85% студентов сдали сессию без двоек, на 2 курсе – 90%. Определить дисперсию доли студентов, успешно сдавших сессию на каждом курсе.

Задача 4.3

Акционерные общества области по среднесписочной численности работающих на 1 января 1998 г. распределились следующим образом.

 

Группы АО по численности работающих	до 400	400-600	600-800	800-1000	1000-1200	1200-1400	1400-1600	1600-1800
Количество АО

 

Рассчитайте:

1) среднее линейное отклонение;

2) дисперсию;

3) среднее квадратическое отклонение;

4) коэффициент вариации.

Задача 4.4

Имеются данные о распределении семей сотрудников предприятия по количеству детей.

 

Число детей в семье	Число семей сотрудников по подразделениям
Первое	Второе	Третье
			-

 

Вычислить:

1) внутригрупповые дисперсии;

2) среднюю из внутригрупповых дисперсий;

3) межгрупповую дисперсию;

4) общую дисперсию.

Проверить правильность проведенных расчетов с помощью правила сложения дисперсий.

Задача 4.5

Распределение стоимости продукции, предназначенной для экспорта по цехам предприятия, представлено следующими данными.

 

Цех	Стоимость всей произведенной продукции (тыс. руб.)	В том числе стоимость экспортной продукции (тыс. руб.)
Итого

 

Вычислить:

1) среднюю из внутригрупповых, межгрупповую и общую доли экспортной продукции;

2) коэффициент детерминации и эмпирическое корреляционное соотношение.

Задача 4.6

По данным обследования коммерческих банков города, 70% общего числа клиентов составили юридические лица со средним размером кредита 120 тыс. руб. и коэффициентом вариации 25%, а 20% – физические лица со средним размером ссуды 20 тыс. руб. при среднем квадратическом отклонении 6 тыс. руб.

Используя правила сложения дисперсий, определите тесноту связи между размером кредита и типом клиента, исчислив эмпирическое корреляционное отношение.

5. Показатели связи

5.1. Методические указания
и решение типовых задач

При статистическом исследовании корреляционных связей основными задачами являются определение на основе регрессионного анализа их формы (математической модели связи) и тесноты связи.

Математическими моделями связи могут быть уравнения регрессии:

линейное – y = a₀ + a₁; (5.1)

степенное – y = a₀ x^a1 ; (5.2)

квадратичное – y = a₀ + a₁ x + a₂ x² и др. (5.3)

Для линейной модели её параметры определяются:

; (5.4)

. (5.5)

Здесь параметр a₁ показывает изменение результативного признака (у) при изменении факторного признака (х) на единицу.

Теснота связи определяется коэффициентом корреляции r. При линейной форме связи он рассчитывается по формуле

. (5.6)

Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности.

Для оценки значимости коэффициента корреляции r применяется t – критерий Стьюдента. При этом фактическое значение критерия t_r:

(5.7)

Вычисленное по формуле (5.7) значение t_r сравнивается с критическим t_кр, которое берется из таблицы значений t критерия Стьюдента с учетом заданного уровня значимости α и числа степеней свободы k.

Если t_r > t_кр, то величина коэффициента корреляции признается существенной.

Для получения выводов о практической значимости синтезированных в анализе моделей показателям тесноты связи дается качественная оценка. Это осуществляется на основе шкалы Чеддока, приведенной в табл. 5.1.

Чем сильнее связь, тем сильнее влияние изучаемого фактора на результативный признак у. При слабой связи вариация результативного признака определяется неучтенными факторами.

Таблица 5.1

Шкала Чеддока

Показатели тесноты связи	Характеристика силы связи
0,1 – 0,3	Слабая
0,3 – 0,5	Умеренная
0,5 – 0,7	Заметная
0,7 – 0,9	Высокая
0,9 – 0,99	Весьма высокая

 

Часто исследуемые признаки имеют разные единицы измерения. Тогда для оценки влияния факторного признака на результативный применяются коэффициент эластичности (Э):

, (5.8)

где – первая производная уравнения регрессии.

Средний коэффициент эластичности определяется для линейного уравнения по формуле

. (5.9)

Он показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1%.

Пример 5.1

Имеются выборочные данные по 10 однородным предприятиям.

 

№ предприятия
Энерговооруженность труда на 1 рабочего, кВт×ч
Выпуск готовой продукции на одного рабочего, т

 

Построить однофакторную регрессионную модель и определить тесноту связи.

Решение

Примем, что факторным признаком (х) является энерговооруженность труда, а результативным (у) – выпуск готовой продукции. Будем считать, что между ними существует линейная связь y = a₀ + a₁ x. Для вычисления параметров модели по формулам (5.4) и (5.5) представим в табл. 5.2 исходные данные и необходимые дополнительные расчетные значения.

Таблица 5.2

Расчет сумм для вычисления параметров уравнения прямой

Исходные данные	Расчетные значения
№ предприятия	х	у	ху	х2	у2
…	…	…	…	…	…
Итого
В среднем	5,0	6,0	34,3	30,4	40,0

 

;

.

 

Линейная модель будет иметь вид

у = 2,02 + 0,796 х. (5.10)

Параметр а ₁ показывает, что с увеличением энерговооруженности труда одного работника на 1 кВт×ч выпуск готовой продукции возрастет на 0,796 т.

Рассчитаем коэффициент корреляции по формуле (5.6):

.

Значение r показывает, что между энерговооруженностью труда и выпуском продукции существует сильная связь.

Средний коэффициент эластичности рассчитывается по формуле (5.9):

,

т.е. с увеличением энерговооруженности труда на 1% выпуск продукции возрастет на 0,66%.

Произведем оценку значимости коэффициента корреляции t по формуле (5.7):

.

С учетом принятых в экономическо-статистических исследованиях значимости α = 0,05 (Р_дов = 0,95) и числа степеней свободы 10 – 2 = 8 табличное значение t_кр= 2,3.

Сравнивая t_расч. и t_кр ,имеем, что t_расч > t_кр., поэтому коэффициент корреляции признается существенным, а синтезированная по уравнению (5.1) математическая модель (5.10) может быть использована для практических целей.

При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, возможно использование так называемых «тетрахорических показателей». Тогда расчетная таблица состоит из четырех ячеек (обозначаемых буквами a, b, c, d). Каждая из клеток соответствует известной альтернативе того или другого признака.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: