 |
Показатель обеспеченности производства запасами
|
|
|
|
, (11.20)
где Одн. – обеспеченность производства запасами в днях;
З – объем фактических запасов материальных ценностей;
Пд – среднедневная потребность в запасах.
2. Коэффициент оборачиваемости оборотных средств характеризует количество оборотов среднего остатка оборотных средств и определяется по формуле
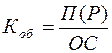, (11.21)
где П(Р) – объем произведенной (реализованной) продукции;
ОС – средний остаток оборотных средств.
3. Коэффициент закрепления оборотных средств характеризует сумму оборотных средств, необходимую для производства (реализации) одного рубля продукции, и определяется по формуле
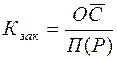. (11.22)
4. Средняя продолжительность одного оборота оборотных средств показывает время (в днях), в течение которого оборотные средства могут обернуться один раз, и определяется по формуле
или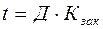 
, (11.23)
где Д – число календарных дней в периоде.
5. Размер высвобожденных оборотных средств из оборотного капитала (привлечения их в оборот) в результате изменения их оборачиваемости в отчетном периоде по сравнению с базисным исчисляется по формуле
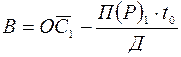или 
, (11.24)
где В – размер высвобожденных (привлеченных) из оборота оборотных средств в результате изменения их оборачиваемости;
П(Р)1 – объем произведенной (реализованной) продукции в отчетном периоде;
t0 – средняя продолжительность одного оборота оборотных средств в базисном периоде;
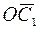– средний остаток оборотных средств в отчетном периоде;
Кзак 0 и Кзак 1 – коэффициенты закрепления оборотных средств в базисном и отчетном периодах.
Пример 11.8
В базисном периоде выручка от продажи продукции, работ, услуг отрасли региона составила 340 млн руб., средний остаток материальных оборотных средств – 34 млн руб. В отчетном периоде выручка от продажи составила 450 млн руб., средний остаток оборотных средств – 30 млн руб. Число календарных дней в базисном и отчетном периодах – 30 дней.
|
|
|
Определить
1. Коэффициенты оборачиваемости оборотных средств.
2. Продолжительность одного оборота в днях.
3. Сумму средств, высвобожденных их оборота в результате ускорения оборачиваемости в отчетном периоде по сравнению с базисным.
Решение
1. Коэффициент оборачиваемости (число оборотов оборотных средств):
;
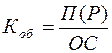оборотов; 
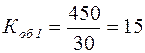оборотов.
2. Продолжительность одного оборота в днях рассчитаем по формуле
;
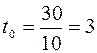дня; 
дня.
Продолжительность одного оборота сократилась на 1 день, или на 33,3%.
2. Сумма средств, высвобожденных из оборота:
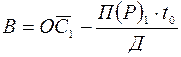или ;
; 
;
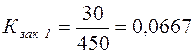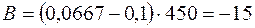млн руб.
11.2. Задачи для самостоятельного решения
Задача 11.1
Имеются следующие данные о наличии и движении основных фондов предприятия за год (в ден. ед.).
1. Полная первоначальная стоимость основных фондов
на начало года 210
2. В течение года:
введено новых 30
выбыло по стоимости за вычетом износа 4
полная первоначальная стоимость выбывших средств 20
3. Износ основных средств на начало года, % 20
4. Годовая норма амортизации, % 10
Определить полную первоначальную стоимость основных фондов на конец года. Построить баланс основных фондов по полной стоимости. Рассчитать показатели, характеризующие движение основных фондов (коэффициенты выбытия и обновления). Рассчитать остаточную стоимость основных средств на начало и конец года. Построить баланс основных фондов по остаточной стоимости. Рассчитать показатели, характеризующие состояние основных фондов, коэффициенты износа и годности.
Задача 11.2
Имеются следующие данные о наличии и движении основных фондов по региону (млн руб.).
1. Полная первоначальная стоимость основных средств
на начало года 1080
2. Сумма их износа 220
3. Поступило за год основных средств 120
|
|
|
4. Выбыло за год 36
5. Сумма износа основных средств на конец года 230
Определить
1. Коэффициенты обновления и выбытия основных средств за год.
2. Коэффициенты износа и годности основных средств на начало и конец года.
Задача 11.3
По предприятию за два полугодия имеются следующие данные.
| Показатели | Базисный период | Отчетный период |
| Выручка от реализации продукции | ||
| Средняя годовая стоимость основных фондов |
Определить
1. Показатели скорости обращения оборотных фондов.
2. Коэффициент закрепления оборотных фондов.
3. Среднюю продолжительность одного оборота.
4. Абсолютное высвобождение оборотных фондов.
Задача 11.4
Объем произведенной продукции в отчетном периоде по сравнению с базисным увеличился на 9% (в сопоставимых ценах). Среднегодовая стоимость основных фондов за этот период возросла в 1.15 раза.
Определите, как изменилась фондоотдача.
Задача 11.5
Среднегодовая стоимость основных фондов в отчетном периоде по сравнению с базовым увеличилась на 12%. Фондоотдача за этот период снизилась на 3%.
Определить, как изменились объем произведенной продукции и ее фондоемкость.
Задача 11.6
В 2000 г. уровень фондоемкости продукции составил 98,8% к ее уровню в 1996 г.
Определить изменение фондоотдачи основных фондов за этот период, ее среднегодовые темпы роста и прирост.
12. Статистика финансов
12.1. Методические указания
и решение типовых задач
Финансово-экономические расчеты представляют собой совокупность методов определения стоимости денег в результате проведения экономических операций. Суть расчетов заключается в исчислении стоимости денег в заданный момент времени в зависимости от определенных условий, к которым относятся время, процентная ставка, условия финансовой операции.
Процентными деньгами, или процентами, называют сумму, которую уплачивают за пользование денежными средствами. Это доход владельца денежных средств. Различают следующие виды процентов:
- обычные и авансовые;
- простые и сложные.
В зависимости от момента выплаты или начисления дохода за пользование предоставленными денежными средствами выделяют обычные и авансовые проценты. Обычные (декурсивные) проценты начисляются в конце периода. Если доход за пользование денежными средствами определяется и выплачивается в момент предоставления кредита, то данная форма расчетов называется авансовой, или учетом, а применяемые при этом проценты – авансовыми (антисипативными). Они начисляются в начале периода.
|
|
|
Наращивание денежных средств может осуществляться по арифметической или геометрической прогрессии. В первом случае проценты начисляются в течение всего срока на первоначальную сумму. Такие проценты называются простыми. Во втором случае база для начисления процентов постоянно меняется за счет присоединения к ней ранее начисленных процентов. Такие проценты называются сложными.
При использовании простых процентов будущая (наращенная) стоимость денег (FV) рассчитывается по следующей формуле:
FV = PV ( 1 +пi), (12.1)
где PV – современная стоимость денег;
n – срок финансовой операции;
I – ставка процента за период.
Эту формулу используют на практике, например, при определении суммы погашения ссуды, предоставленной под простые проценты, размера срочного вклада с процентами.
Пример 12.1
Банк выдал ссуду 100 д.е. (РV = 100 д.е.) на два гола (п = 2) под 10% годовых (i = 0,1). Определим подлежащую возврату сумму (FV), если начисляются простые проценты в конце каждого гола, а долг гасится единовременным платежом в конце второго года.
FV= РV( 1 + пi) = 100 (1+ 2·0,1) = 120 д.е. (12.2)
Дисконтирование, или учет, – это определение современной стоимости денег (РV) на основе будущей (FV). В этих расчетах величина РV называется приведенной стоимостью суммы FV.
Расчет современной стоимости денежных средств, предоставляемых в долг, проводят по формуле
.
Пример 12.2
Ставка размещения денежных ресурсов на три года (n = 3) составляет 20% (i = 0,20). Какой объем средств необходимо разместить, чтобы в конце операции получить 10 д.е. (FV = 10 д.е.)?
д.е.
Наряду с простыми процентами в практике расчетов используются сложные. В этом случае стоимость, на которую начисляются проценты, постоянно меняется. Процесс расчета наращенной суммы с учетом присоединения к ней дохода, полученного за предыдущий период, называется капитализацией, или реинвестированием.
|
|
|
По ставке декурсивных процентов i расчет наращенной суммы к концу периода n проводится по формуле
FV = PV ( 1 +i)”. (12.3)
Пример 12.3
В банк на срочный вклад помещены денежные средства в размере 30 д.е. (PV = 30 д.е.). Условием договора предусмотрено, что вклад может быть востребован через три года (n = 3), за что банк обязуется ежегодно начислять 15% годовых.(i = 0,15) по схеме сложных процентов. Определим, сколько вкладчик получит через три года, если банк выполнит свои обязательства?
FV= РV ( 1 +i) = 30 (1+ 0,15)³ = 45,63 д.е.
Расчет современной стоимости денег по сложной процентной ставке осуществляют по формуле
. (12.4)
В приведенных выше формулах (1 +i)” и 
называются соответственно множителем наращения и дисконтирующим множителем. Для практических расчетов имеются специальные таблицы, в которых приводятся значения этих коэффициентов в зависимости от размера ставки и периода наращения.
Пример 12.4
Определим, сколько необходимо внести в банк, чтобы через три года получить сумму, равную 45,63 д.е. (FV= 45,63), если процентная ставка равна 15% годовых (i = 0,15). По таблице находим дисконтирующий множитель [2] для заданных условий. Он равен 0,657516232.
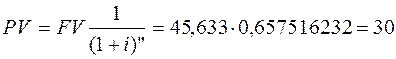д.е.
12.2. Задачи для самостоятельного решения
Задача 12.1
Банк выдал ссуду 250 д.е. на 2 года под 15% годовых.
Определить сумму, подлежащую возврату, если начисляются простые проценты в конце каждого года.
Задача 12.2
Какую ссуду можно взять в банке на 3 года под 10% годовых, если возврат через 3 года может составлять не более 300 ден. единиц.
(Начисление простых процентов происходит в конце каждого года.)
Задача 12.3
Ставка размещения денежных средств на 2 года составляет 10% в год. Какой объем средств необходимо вложить в банк, чтобы в конце операции получить 100 д.е.?
Задача 12.4
Денежные средства вложены в банк на 2 года под 25% годовых, начисляемых ежегодно по схеме сложных процентов. Сколько получит вкладчик через 2 года, если он вложил 100 д.е.?
Задача 12.5
Под какой процент следует вложить в банк 10 д.е. на 2 года, если начисления будут производиться ежегодно по схеме сложных процентов?
13. Статистика рынка товаров и услуг
13.1. Методические указания
и решение типовых задач
Конъюнктура рынка – это совокупность условий, определяющих рыночную ситуацию. Конъюнктура характеризуется спросом и предложением.
Спрос – это количество товаров и услуг, которое будет куплено по определенной цене за определенный период. Спрос – это также требование на какой-либо товар со стороны покупателя или на рабочую силу со стороны работодателя.
Предложение – количество товаров и услуг, которое производители готовы продать по определенной цене за определенное время.
|
|
|
Спрос и предложение взаимосвязаны: спрос порождает предложение, но и предложение некоторым образом влияет на спрос. Соотношение спроса и предложения на рынке постоянно меняется в зависимости от совокупности экономических, социально-политических, демографических и других факторов.
Одной из характеристик этой взаимосвязи является эластичность спроса и предложения.
Эластичность спроса – это мера реакции одной величины на изменение другой (например, изменение спроса на товар (%) в зависимости от изменения цены на 1%).
Эластичность предложения характеризует, например, как реагирует производство той или иной продукции на изменение цены.
Мера эластичности выражается коэффициентом эластичности, т.е. процентным изменением одного (результативного) признака при изменении на 1% другого (факторного) признака.
Формула коэффициента эластичности предложена английским исследователем Э. Маршаллом:
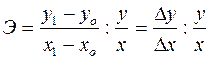, (13.1)
где ∆у = у1 – у0 –прирост спроса;
∆х = х1 – х0 – прирост факторного признака;
у –базовый показатель;
х –базовое значение факторного признака.
При Э < 1 проявляется явление инфраэластичности, товар считается малоэластичным или неэластичным.
При Э > 1 – ультраэластичность, товар является эластичным или сильноэластичным.
При Э = 1 товар является слабоэластичным, единично эластичным (так называемый унитарный спрос), в этом случае снижение цены не приводит к коммерческому результату (росту выручки), т.е. изменение одного признака вызовет такое же изменение другого признака.
Положительное значение коэффициента эластичности означает, что при увеличении факторного признака спрос растет, т.е. связь прямая.
Отрицательное значение коэффициента эластичности означает, что при увеличении факторного признака спрос сокращается, т.е. связь обратная.
Эластичный спрос по цене
, (13.2)
где ∆Q – изменение величины спроса (%);
∆Р – изменение цены (%).
Показатель ценовой эластичности спроса для всех товаров – величина отрицательная (цена снижается – спрос растет). Однако для оценки эластичности знак «минус» опускается.
Измерить эластичность спроса по цене можно также по формуле
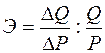. (13.3)
Первая формула позволяет определить, эластичен, неэластичен, единично эластичен товар, прямая или обратная связь между признаками.
Вторая формула показывает, что показатель эластичности зависит не только от соотношения приростов цены и спроса (∆Q и ∆Р), но и от их фактических значений (Р и Q).
При эластичном спросе снижение цены и рост объемов продаж (спроса) приводят к увеличению общей величины выручки от реализации, при неэластичном спросе – к уменьшению выручки от реализации.
Эластичность спроса по доходу измеряется как отношение изменения спроса на товар (∆Q) к изменению доходов потребителей (∆Р):
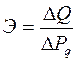. (13.4)
Измерив эластичность по доходу, можно определить, относится ли данный товар к категории нормальных (когда рост доходов приводит к росту спроса) или к категории низших (когда рост доходов приводит к снижению спроса, например продукция «Sekond hand»). В первом случае Э, > 1, во втором случае Э,< 1.
Эластичность предложения – это реакция производства на изменение цены.
При единичной эластичности предложения 1% увеличения цены вызывает 1% увеличения количества предлагаемого к продаже товара (Эq = 1).
При эластичном предложении 1% увеличения цены способен вызвать увеличение количества предлагаемого к продаже товара более чем на 1% (Эq > 1).
При неэластичном предложении увеличение цены не оказывает какого-либо влияния на увеличение количества предлагаемых к продаже товаров (Эq < 1).
Коэффициент эластичности предложения
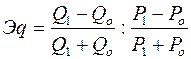; (13.5)
где Qо, Q1 – предложение до и после изменения цены:
Ро, Р1 – цены до и после изменения.
На макроуровне мы имеет дело не с индивидуальным спросом и предложением одного конкретного товара, а с совокупным спросом и предложением в рамках национального рынка.
Конкретные разнородные товары объединяются в совокупную массу товаров, выражаемую не в виде натуральных единиц измерения, а в виде совокупной цены. А спрос выступает не как спрос отдельных покупателей, а как совокупный платежеспособный спрос в масштабе всего народного хозяйства.
Таким образом, совокупный спрос – это спрос на общий объем товаров и услуг, который может быть предъявлен при данном уровне цен, т.е. при данной платежеспособности. Совокупный спрос – это спрос на потребительские и инвестиционные товары.
Совокупное предложение – это общее количество товаров и услуг, которое может быть произведено и предложено в соответствии со сложившимся уровнем цен. Таким образом, совокупное предложение равно валовому внутреннему продукту.
Для измерения объема и динамики совокупного спроса и совокупного предложения используются агрегатные индексы.
Товародвижение – процесс движения товара от производителя к конечному покупателю. Товародвижение может быть организовано по различным каналам распределения, в том числе напрямую (производитель – потребитель) и через сеть посредников (торговых агентов, брокеров).
Товарооборот – это объем реализованной продукции в стоимостном выражении (Q):
Q = q · p. (13.6)
Товарооборот может быть:
а) валовым – сумма всех продаж на пути движения от производителя к потребителю. Размер валового товарооборота прямо пропорционален числу перепродаж, т.е. он включает повторный счет и не отражает реального объема проданных товаров;
б) чистым – это валовой товарооборот, освобожденный от повторного счета. Чистый товарооборот равен конечной продаже товара, т.е. партии товара, которая больше продаваться не будет;
в) оптовым – это продажа товара крупными партиями производителями и торговыми посредниками другим посредникам для последующей перепродажи;
г) розничным – это продажа товаров предприятиям для конечного потребления.
Одним из показателей, характеризующих товарооборот, является коэффициент зависимости. Это показатель числа перепродаж (числа звеньев) товара:
. (13.7)
Этот расчет будет верным при условии, что все товары, влившиеся в сферу обращения без потерь и изменения товарных запасов, дошли до конечного звена. Этого практически не бывает. Поэтому расчет коэффициента звенности должен корректироваться на величину изменения товарных запасов (потерь). Если имеются сведения о товарных запасах на начало и конец периода, то изменение их определяется по формуле
∆З = Зк + Зн ,(13.8)
где Зк – запасы на конец периода;
Зн –запасы на начало периода.
Если З к > З и, то ∆З > 0(запасы растут).
Если Зк < Зн,, то ∆З < 0 (запасы сокращаются).
Если Зк = Зн,, то ∆З = 0 (изменений в запасах нет).
Если нет прямых сведений о запасах, пользуются балансовой формулой движения товаров:
Зн + П = Р + Зк ,(13.9)
где Зк – запасы на конец периода;
Зн – запасы на начало периода;
П –поступления товаров в сферу обращения;
Р –реализация товаров за этот же период.
Отсюда
∆З = Зк – Зн = П – Р (13.10)
Если П > Р, то ∆З > 0 (рост товарных запасов).
П < Р, то ∆З < 0 (запасы сокращаются).
П = Р, то ∆З = 0 (изменений в запасах нет).
В итоге коэффициент звенности с учетом поправок на изменение запасов
. (13.11)
В практике анализа товарооборота широко используется индексный метод, в частности индексы переменного состава:
(13.12)
и индексы постоянного состава, которые характеризуют изменение товарооборота под влиянием:
а) фактора физического объема продаж
; (13.13)
б) фактора цен на реализованную продукцию
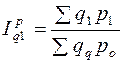. (13.14)
Особое место занимают индексы товарооборота на душу населения
. (13.15)
Индексы (13.12), (13.13), (13.14) связаны между собой соотношением
. (13.16)
Выражение ∆pq = ∆pqp + ∆pqq (13.17)
дает представление о приросте товарооборота за счет количественного (q) и ценного (p) факторов.
На макроуровне товарооборот представляет собой произведение душевого потребления (Д) на численность населения
Sqp = SД · Т. (13.18)
Прирост товарооборота
∆pq = SД 1· Т1 – SД о· Тp. (13.19)
Преобразуем выражение (13.18)
∆pq = SД 1· Т1 – SД о· То + SД о· Т1 – SД о· Тp =
= (SД 0· Т1 – SД о· То) + (SД 1· Т1 – SД о· Т1),
тогда
∆pq = ∆pqТ + ∆pqД. (13.20)
Постоянное наличие на рынке некоторой товарной массы обеспечивает непрерывность процесса производства. Эта масса товаров представляет собой запас.
Существует следующая система показателей товарных запасов.
1. Объем товарных запасов в натуральном и стоимостном выражении.
2. Структура товарных запасов, т.е. доля отдельных товаров и товарных групп в общем объеме товарных запасов.
3. Средние товарные запасы. В зависимости от объема информации средние товарные запасы могут быть определены разными способами:
а)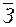 
= 
(13.21)
– среднемесячные запасы, если имеются данные о запасах на начало и конец периода;
б) =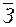 
(13.22)
– средние запасы за более длительный срок, чем месяц, по данным на конец каждого месяца.
4. Запасаемость характеризует, сколько товарных запасов приходится на единицу товарооборота:
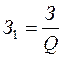. (13.23)
5. Обеспеченность товарооборота товарными запасами (дн.), т.е. число дней торговли, на которые хватает товарных запасов до момента их полного истощения:
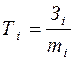, (13.24)
где Тi – обеспеченность товарооборота i -того товара запасами i -тоготовара;
3i – товарные запасы i -того товара.
Однодневный товарооборот (mi) составляет величину
(13.25)
Товарооборачиваемость – это кругооборот товарной массы, представляет собой законченный процесс вовлечения товара в сферу товарного обращения и переход в сферу потребления.
Показатели товарооборачиваемости.
1. Скорость товарного обращения – число оборотов (продаж), через которое прошел товар, находясь в сфере обращения:
, (13.26)
где С – скорость обращения i -того товара;
Q – объем товарооборота;
– средние товарные запасы.
2. Время одного оборота – число дней, в течение которых товар находится в форме товарного запаса:
. (13.27)
|
|
|
