Коэффициент износа и годности основных фондов на конец года 4 глава

 

	Да	Нет
Да	a	b
Нет	c	d

 

Для такого рода таблиц построен ряд показателей: коэффициент ассоциации и коэффициент контингенции.

Пример 5.2

Оценить наличие связи между работниками торговли, распределенными по полу и содержанию работы. Результаты исследования сведены в статистическую таблицу (табл. 5.3).

Таблица 5.3

Распределение работников торговли
по полу и оценке содержания работы

Работа	Мужчины	Женщины	Всего
Интересная	300 (а)	201 (b)	501 (a+b)
Неинтересная	130 (c)	252 (d)	381 (c+d)
Итого	430 (a+c)	453 (b+d)	883 (a+b+c+d)

 

Коэффициент ассоциации К_а определяется по формуле

. (5.11)

В приведенном примере его величина будет равна 0,486:

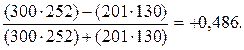
Величина коэффициента в нашем примере соответствует среднему размеру связи, несмотря на различие мнений о своей работе мужчин и женщин.

Коэффициент контингенции К_к рассчитывается по формуле

(5.12)

Связь считается подтвержденной, если К_а > 0,5 или К_к > 0,3.

Пример 5.3

Исследовалась социально-демографическая характеристика случайных потребителей наркотиков в зависимости от их семейного положения в одном из регионов РФ (тыс. чел.). Результаты обследования характеризуются следующими данными

 

Группы потребителей наркотиков	Семейное положение	Всего
Замужем (женат)	Не замужем (не женат)
Потреблял Не потреблял	10,0 2,5	14,5 4,5	24,5 7,0
Итого	12,5	19,0	31,5

 

Рассчитать коэффициенты ассоциации и контингенции.

Решение

;

Вывод. Так как К_а < 0,5 и К_к < 0,3, то потребление наркотиков случайными потребителями не зависит от их семейного положения.

Для определения тесноты связи как между количественными, так и между качественными признаками при условии, что значения этих признаков могут быть упорядочены, или проранжированы по степени убывания или возрастания признака, может быть использован коэффициент Спирмена (коэффициент ранговой корреляции) Р, который рассчитывается по следующей формуле:

, (5.13)

где – квадраты разности рангов связанных величин х и у;

;

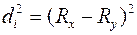N – число наблюдений (число пар рангов).

Ранг – это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин.

Пример 5.4

Рассмотрим наличие связи между обеспеченностью товарной продукцией ряда предприятий и накладными расходами по реализации (табл. 5.4).

Таблица 5.4

 

Обеспеченность товарной продукцией, млн руб. х	Наклад-ные расходы по реализации, тыс. руб. у	Ранжирование	Сравнение рангов	Разность рангов
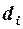
x	ранг	y	ранг
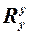
12,0 18,8 11,0 29,0 17,5 23,4 35,6 15,4 26,1 20,7		11,0 12,0 15,4 17,5 18,8 20,7 23,4 26,1 29,0 35,0						-1 -1 -1 -1 -5
Итого

По данным табл. 5.4 получим следующие значения коэффициента Спирмена:

Пользуясь определением тесноты связи по шкале Чеддока, можно сказать, что полученная связь – заметная.

Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции w (или коэффициент конкордации), который вычисляется по формуле

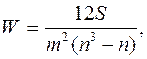(5.14)

где m – количество факторов;

n – число наблюдений;

S – отклонение суммы квадратов рангов от средней квадратов рангов.

Пример 5.5

Определить тесноту связи между уставным капиталом, числом выставленных акций и числом занятых на предприятиях, выставивших акции на чековые аукционы в 1998 г. (табл. 5.5).

Таблица 5.5

Расчет коэффициента конкордации (данные условия)

№ предприятия	Уставный капитал, тыс. руб. Х	Число выставленных акций У	Число занятых на предприятии Z				Сумма рангов	Квадраты сумм
	2 954 1 605 4 102 2 350 2 625 1 795 2 813 1 751 1 700 2 264
-	-	-	-	-	-	-		2 863

Коэффициент конкордации говорит о том, что связь между заданными параметрами слабая.

5.2. Задачи для самостоятельного решения

Задача 5.1

Имеются данные по группе однородных предприятий.

 

№ предприятия
Основные фонды (ден. ед)
Продукция (ден. ед)	9,9	10,8	11,5	12,0	12,4

 

1. Построить управление линейной корреляционной зависимости продукции от основных фондов.

2. Вычислить коэффициент эластичности.

3. Вычислить линейный коэффициент корреляции.

4. Сделать выводы.

Задача 5.2

По пяти однородным предприятиям имеются следующие данные.

№ предприятия
Количество рабочих с профессиональной подготовкой, %
Количество бракованной продукции, %

 

По исходным данным построить однофакторную линейную модель зависимости между выпуском бракованной продукции и профессиональной подготовкой рабочих.

Вычислить коэффициент эластичности и показатель тесноты корреляционной связи.

6. Ряды динамики

6.1. Методические указания
и решение типовых задач

Числовые значения того или иного статистического показателя, составляющие ряд динамики, называют уровнями ряда и обозначают через y.

При анализе рядов динамики, чтобы проследить за направлением и размером изменений уровней во времени, рассчитывают следующие показатели:

абсолютные приросты уровней (разность между двумя уровнями):

цепные Dу_ц = уi – у_i-1 (6.1)

и базисные Dу_б = уi –у₀; (6.2)

темпы роста (изменения) ТР – относительные показатели, рассчитываемые как отношение двух уровней ряда. Темпы роста могут быть цепными, если каждый уровень сопоставляется с предыдущим

, (6.3)

и базисными, когда все уровни сопоставляются с уровнем одного какого-то периода (часто это начальный уровень ряда):

. (6.4)

Темпы роста как относительные величины могут выражаться в виде коэффициентов, т.е. простого кратного отношения (база сравнения принимается за единицу), и в процентах (база сравнения принимается за 100 единиц).

Темпы прироста (снижения) уровней ТПр – относительные показатели, показывающие, на сколько процентов данный уровень (y) больше (или меньше) другого, принимаемого за базу сравнения.

Темп прироста можно рассчитать двояко:

1) путем вычитания 100% из темпа роста:

ТПр =ТР -100%;(6.5)

2) как процентное отношение абсолютного прироста к тому уровню, по сравнению с которым рассчитан абсолютный прирост:

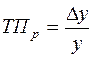. (6.6)

Очень важно правильно определять средние значения показателей динамики.

В качестве обобщенной характеристики для определенного периода рассчитывается средний уровень ряда (y).

В интервальном ряду абсолютных величин средний уровень рассчитывается как средняя арифметическая простая:

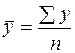, (6.7)

где п – число уровней ряда.

Для интервального ряда с разными временными интервалами средний уровень определяется по формуле

, (6.8)

где t_i – время, в течение которого уровень y считается неизменным.

Для моментного ряда, содержащего n уровней с равными промежутками между датами (моментами), средний уровень определяется по формуле

. (6.9)

Эта средняя известна в статистике как средняя хронологическая для моментных рядов.

Для равностоящих уровней моментального ряда:

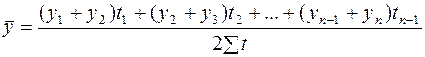. (6.10)

Средний абсолютный прирост определяется по формуле

(6.11)

или , (6.12)

где п – число периодов.

Средний темп роста определяется из выражения

, (6.13)

где п – число темпов роста, а П – знак произведения.

(6.14)

Средний темп прироста определяется по формуле

. (6.15)

Абсолютное значение одного процента прироста (А1%) рассчитывается как

, (6.16)

или А1% может быть исчислен как одна сотая часть предыдущего уровня.

Среднее абсолютное значение одного процента прироста за несколько (п) лет определяются по формуле

. (6.17)

Пример 6.1

Пусть о производстве зерна в одном из хозяйств за 5 лет имеются следующие данные.

Год
Производство зерна, тыс. ц. уi

Рассчитать:

1) средний уровень за 5 лет;

2) ежегодные абсолютные приросты;

3) ежегодные темпы роста;

4) среднегодовой темп роста за 4 года, с 1994 по 1997 г.

Решение

1. Так как это интервальный ряд, то средний уровень ряда (среднегодовое производство зерна) определим как среднюю арифметическую простую:

тыс. ц.

2. Ежегодные абсолютные приросты находим как разность между двумя уровнями:

Для 1994 г. Δ у1 = 54 – 50 = 4 тыс. ц;

Для 1995 г. Δ у2 = 62 – 54 = 8 тыс. ц;

Для 1996 г. Δ у3 = 70 – 62 = 8 тыс. ц;

Для 1997 г. Δ у4 = 80 –70 = 10 тыс. ц.

3. Ежегодные темпы роста (цепные) находим как отношение уровня каждого года к предыдущему:

Для 1994 г. ТР1 = 54 / 50 = 1,08 = 108%;

Для 1995 г. ТР2 = 62 / 54 = 1,148 = 114,8%;

Для 1996 г. ТР3 = 70 / 62 = 1,129 = 112,9%;

Для 1997 г. ТР4 = 80 / 70 = 1,143 = 114,3%.

4. Среднегодовой темп роста можно рассчитать как среднюю геометрическую из годовых темпов роста:

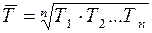
либо по формуле

.

По первой формуле

.

По второй формуле

,

т.е. среднегодовой темп роста за 4 года (с 1994 по 1997 г.) равен 112,5%.

Пример 6.2

Определить срок, за который ряд с большим средним показателем динамики, но меньшим начальным уровнем, догонит другой ряд с меньшим средним показателем динамики, но с большим начальным уровнем.

Преобразуем формулу (6.14), обозначив через :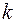

.

Тогда

.

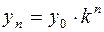Необходимо определить, когда

.

Решение

.

Прологарифмируем:

Отсюда

.

Если , и , ,

то .

Следовательно, через 11 лет уровень 11 ряда сравнивается с уровнем 1 ряда.

6.2. Задачи для самостоятельного решения

Задача 6.1

О производстве картофеля в хозяйствах населения РФ за 1991-1996 гг. имеются следующие данные.

 

Год
Производство картофеля, млн т	24,8	29,9	31,1	29,8	35,9	34,9

 

Определить:

1) абсолютные приросты производства картофеля по годам (цепные);

2) цепные и базисные коэффициенты роста;

3) среднегодовой уровень производства картофеля за 1991-
1996 гг.;

4) среднегодовой коэффициент роста производства картофеля в хозяйствах населения за 1992-1996 гг.

Задача 6.2

Об остатках наличных денег у населения РФ в первой половине 1997 г. имеются следующие данные.

 

Месяц	Январь	Февраль	Март	Апрель	Май	Июнь	Июль
Остаток денег на начало месяца, трлн руб.	75,8	70,5	74,5	77,1	84,7	88,4	100,5

 

Рассчитать:

1) средний остаток наличных денег у населения за январь – июнь;

2) среднемесячный темп роста наличных денег у населения за 6 месяцев 1997 г.

Задача 6.3

О мировых ценах на кофе в Бразилии (за 1 кг) имеются следующие данные.

 

Год
Цена, $	1,3	1,27	0,95	1,1	2,55	2,73	2,21

 

1) рассчитать основные аналитические показатели ряда динамики (абсолютные приросты, темпы роста и др.);

2) определить уравнение тренда мировых цен на кофе.

Задача 6.4

Производство шерсти в фермерских хозяйствах РФ характеризуется следующими данными.

Год
Произведено тыс. т	1,4	2,9	3,3	4,2	3,6

 

1) определить среднегодовой темп роста производства шерсти за 1993-1996 гг.

2) провести аналитическое выравнивание уровней ряда и на основе уравнения тренда спрогнозировать производство шерсти в 1999 г.

Задача 6.5

О динамике валового внутреннего продукта (ВВП) РФ имеются следующие данные (в сопоставимых ценах).

 

Год
ВВП % к предыдущему году		85,5	91,3	87,3	95,9	96,6	100,9	95,4

 

1. Определить процент изменения ВВП в 1998 г. по сравнению с 1990 г.

2. Рассчитать среднегодовой темп изменения ВВП за 1991-1998 гг.

7. Выборочное наблюдение

7.1. Методические указания
и решение типовых задач

Целью выборочного наблюдения является определение характеристик генеральной совокупности – генеральной средней () и генеральной доли (р). Характеристики выборочной совокупности – выборочная средняя () и выборочная доля () отличаются от генеральных характеристик на величину ошибки выборки (). Поэтому для определения характеристик генеральной совокупности необходимо вычислять ошибку выборки, или ошибку репрезентативности, которая определяется по формулам, разработанным в теории вероятностей для каждого вида выборки и способа отбора.

Собственно случайная и механическая выборки. При случайном повторном отборе предельная ошибка выборки для средней () и для доли () определяется по формулам

; (7.1)

(7.2)

где – дисперсия выборочной совокупности;

n – численность выборки;

t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной вероятности (P_дов.).

При бесповторном случайном и механическом отборе предельная ошибка выборки определяется по формулам

; (7.3)

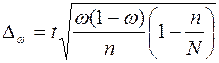, (7.4)

где N – численность генеральной совокупности.

Пример 7.1

Для определения зольности угля в месторождении в порядке случайной выборки было обследовано 100 проб угля. В результате обследования установлено, что средняя зольность угля в выборке – 16%, среднее квадратическое отклонение – 5%. В десяти пробах зольность угля составила более 20%. С вероятностью 0,954 определить пределы, в которых будут находиться средняя зольность угля в месторождении и доля угля с зольностью более 20%.

Решение

Средняя зольность угля будет находиться в пределах

.

Для определения границ генеральной средней вычислим предельную ошибку выборки для средней по формуле (7.1):

. (7.5)

С вероятностью 0,954 можно утверждать, что средняя зольность угля в месторождении будет находиться в пределах 16% 1%, или 15% 17%.

Доля угля с зольностью более 20% она будет находиться в пределах

.

Выборочная доля определяется по формуле

, (7.6)

где m – доля единиц, обладающих признаком

.

Ошибку выборки для доли () вычислим по формуле (7.2):

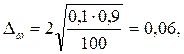или 6%.

С вероятностью 0,954 можно утверждать, что доля угля с зольностью более 20% в месторождении будет находиться в пределах , или .

Пример 7.2

Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 5%-ная механическая выборка, в которую попало 100 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении 9 дней. В пяти счетах срок пользования кредитом превышал 60 дней. С вероятностью 0,954 определить пределы, в которых будут находиться срок пользования краткосрочным кредитом в генеральной совокупности и доля счетов со сроком пользования краткосрочным кредитом более 60 дней.

Решение

Средний срок пользования кредитом в банке находится в пределах

.

Так как выборка механическая, то ошибка выборки определяется по формуле (7.1):

дня.

С вероятностью 0,954 можно утверждать, что срок пользования краткосрочным кредитом в банке находится в пределах =30 дней 2 дня, или 28 дней дня.

Доля кредитов со сроком пользования более 60 дней находится в пределах

.

Выборочная доля составит величину

Ошибку выборки для доли определим по формуле (7.2):

или 4,2%.

С вероятностью 0,954 можно утверждать, что доля кредитов в банке со сроком пользования более 60 дней будет находиться в пределах или

Типическая выборка. При типическом (районированном) отборе генеральная совокупность разбирается на однородные типические группы, районы. Отбор единиц наблюдения в выборочную совокупность производится различными методами. Рассмотрим типическую выборку с пропорциональным отбором внутри типических групп.

Объем выборки из типической группы при отборе, пропорциональном численности типических групп, определяется по формуле

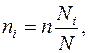(7.7)

где n_i – объем выборки из типической группы;

N_i – объем типической группы.

Предельная ошибка выборочной средней и доли при бесповторном случайном и механическом способе отбора внутри типических групп рассчитывается по формулам

; (7.8)

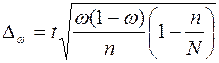, (7.9)

где – дисперсия выборочной совокупности.

Пример 7.3

Для определения среднего возраста мужчин, вступающих в брак, в районе была произведена 5%-ная типическая выборка с отбором единиц пропорционально численности типических групп. Внутри групп применялся механический отбор.

 

Социальная группа	Число мужчин	Средний возраст	Среднее квадратическое отклонение	Доля мужчин, вступающих во второй брак, %
Рабочие
Служащие

 

С вероятностью 0,954 определить пределы, в которых будет находиться средний возраст мужчин, вступающих в брак, и долю мужчин, вступающих в брак во второй раз.

Решение

Средний возраст вступления в брак мужчин находится в пределах

.

Средний возраст вступления в брак мужчин в выборочной совокупности определим по формуле средней взвешенной

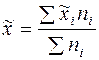; (7.10)

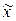= года.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: