 |
Коэффициент износа и годности основных фондов на конец года 5 глава
|
|
|
|
Выборочная дисперсия определяется по формуле средней взвешенной
; (7.11)
= 
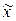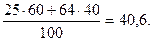
Предельную ошибку выборки вычислим по формуле (7.8):
года.
С вероятностью 0,954 можно утверждать, что средний возраст мужчин, вступающих в брак, будет находиться в пределах 
года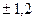 
года, или 24 года 
года.
Доля мужчин, вступающих в брак во второй раз, будет находиться в пределах
.
Выборочную долю определим по формуле средней взвешенной:
или 14%.
Выборочную дисперсию альтернативного признака вычисляем по формуле
(7.12)
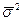
Ошибку выборки для доли определим по формуле (7.9):
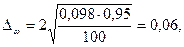или 6%.
С вероятностью 0,954 можно утверждать, что доля мужчин, вступающих в брак во второй раз, будет находиться в пределах 
, или 
.
Серийная выборка. При серийном способе отбора генеральную совокупность делят на одинаковые по объему группы – серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию.
При бесповторном отборе серий предельные ошибки выборочной средней и доли определяются по формуле
, (7.13)
где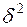 
– межсерийная дисперсия;
R – число серий в генеральной совокупности;
r – число отобранных серий.
Пример 7.4
В цехе предприятия 10 бригад рабочих. С целью изучения производительности их труда была осуществлена 20%-ная серийная выборка, в которую попали 2 бригады. В результате обследования установлено, что средняя выработка рабочих в бригадах составила 4,6 и 3 т. С вероятностью 0,997 определить пределы, в которых будет находиться средняя выработка рабочих цеха.
Решение
Средняя выработка рабочих цеха будет находиться в пределах
.
Выборочную среднюю серийной выработки определим по формуле (3.1):
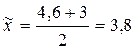т.
Дисперсию серийной выборки определим по формуле
|
|
|
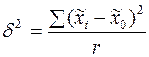, (7.14)
где 
– выборочная средняя серии;
– выборочная средняя серийной выборки.
Значение дисперсии составляет
.
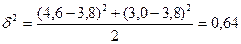Рассчитаем предельную ошибку выборки для средней по формуле (7.13):
т.
С вероятностью 0,997 можно утверждать, что средняя выработка рабочих цеха находится в пределах 
т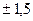 
т, или 2,3 т 
т.
Пример 7.5
На складе готовой продукции цеха находится 200 ящиков деталей по 40 штук в каждом ящике. Для проверки качества готовой продукции была произведена 10%-ная серийная выборка. В результате выборки установлено, что доля бракованных деталей составляет 15%. Дисперсия серийной выборки равна 0,0049.
С вероятностью 0,997 определить пределы, в которых находится доля бракованной продукции в партии ящиков.
Решение
Доля бракованных деталей будет находиться в пределах
.
Определим предельную ошибку выборки для доли по формуле (7.13):
или 4,4%.
С вероятностью 0,997 можно утверждать, что доля бракованных деталей в партии находится в пределах 10,6% 
19,6%.
В практике проектирования выборочного наблюдения возникает потребность в нахождении численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик – средней и доли.
При этом предельная ошибка выборки, вероятность ее появления и вариация признака предварительно известны.
При случайном повторном отборе численность выборки определяется по формуле
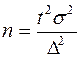. (7.15)
При случайном бесповторном и механическом отборе численность выборки вычисляется по формуле
. (7.16)
Для типической выборки
. (7.17)
Для серийной выборки
. (7.18)
Пример 7.6
В районе проживает 2000 семей. Предполагается провести их выборочное обследование методом случайного бесповторного отбора для нахождения среднего размера семьи. Определить необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки не превысит одного человека при среднем квадратическом отклонении в три человека.
|
|
|
Решение
При бесповторном случайном отборе численность выборки по формуле (7.16) составит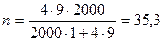 
семей.
Численность выборки: не менее 36 семей.
Пример 7.7
В городе А проживает 10 000 семей. С помощью механической выборки предполагается определить долю семей с тремя детьми и более. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,02, если на основе предыдущих обследований известно, что дисперсия равна 0,2.
Решение
Определим необходимую численность выборки по формуле (7.16):
.
Численность выборки: не менее 1667.
7.2. Задачи для самостоятельного решения
Задача 7.1
При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия, равный 30 г, при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите интервалы, в которых находится средний вес изделия в генеральной совокупности.
Задача 7.2
В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по количеству детей.
| Число детей в семье | ||||||
| Количество семей |
С вероятностью 0,954 установите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Задача 7.3
С целью определения средней фактической продолжительности рабочего дня в государственных учреждениях с численностью служащих 480 человек в июне 1996 г. была проведена 25%-ная механическая выборка. По результатам наблюдений оказалось, что у 10% обследованных потери времени достигали более 45 мин в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин в день.
При серийной выборке средняя ошибка определяется следующим образом:
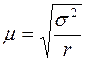– повторный отбор;
– бесповторный набор,
где R – число серий в генеральной совокупности,
r – число серий в выборочной совокупности,
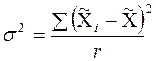– межгрупповая (межсерийная) дисперсия.
Задача 7.4
В области, состоящей из 20 регионов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5; 16; 15,5; 15 и 14 ц/га. С вероятностью 0,954 найдите пределы урожайности во всей области.
|
|
|
Приведем наиболее часто используемые на практике выражения необходимого объема выборки:
собственно случайная и механическая выборка
– повторный отбор;
– бесповторный отбор,
типическая выборка
– повторный отбор;
– бесповторный отбор,
серийная выборка
– повторный отбор;
– бесповторный отбор.
Здесь r – число серий в выборочной совокупности.
Задача 7.5
В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225?
Задача 7.6
С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. человек, в том числе 7 тыс. мужчин и 5 тыс. женщин.
На основе предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.
Задача 7.7
В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обслуживания рабочих, если ошибка выборки не должна превышать 5%.
8. Экономические индексы
8.1. Методические указания
и решение типовых задач
Индекс в статистике – это обобщающий показатель сравнения двух совокупностей, состоящих из элементов, непосредственно не поддающихся суммированию.
Переход от натурально-вещественной формы выражения товарных масс к стоимостной является основой индексного метода. Именно денежное выражение стоимости отдельных товаров устраняет их несуммируемость.
|
|
|
Индивидуальные индексы характеризуют изменения отдельных единиц статистической совокупности.
Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц, образующих статистическую совокупность.
Индивидуальные индексы принято обозначать i, а общие – I.
Основным элементом индексного отношения является индексируемая величина. Под индексируемой величиной понимается значение признака статистической совокупности, изменение которой является объектом изучения. Так, при изучении изменения цен индексируемой величиной является цена единицы товара р. При изучении изменения физического объема товарной массы в качестве индексируемой величины выступают данные о количестве товаров в натуральных измерителях q.
Индивидуальные индексы физического объема реализации товаров iq определяются по формуле
(8.1)
где q1 и q0 – количество продажи отдельной товарной разновидности в текущем и базисном периодах. Индивидуальный индекс показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным.
Для определения индивидуальных индексов цен ip применяется формула
, (8.2)
где p1 и p0 – цены за единицу товара в текущем и базисном периодах.
Общие индексы характеризуют изменения совокупности в целом и могут исчисляться как по агрегатной, так и по средней форме (среднего арифметического или среднего гармонического индекса). Выбор формы общих индексов зависит от характера исходных данных.
Агрегатный индекс – основная форма всякого экономического индекса.
Индекс стоимости продукции, или товарооборота (Ipq), представляет собой отношение стоимости продукции текущего периода (Σp1q1) к стоимости продукции в базисном периоде (Σp0q0) и определяется по формуле
. (8.3)
Такой индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным.
Разность числителя и знаменателя (Σp1q1 – Σp0q0) показывает, на сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным.
Индекс физического объема продукции (Iq) –это индекс количественного показателя. В этом индексе индексируемой величиной является количество продукции в натуральном выражении, а весом (соизмерителем) – цена.
Формула индекса примет следующий вид:
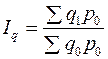. (8.4)
Индекс цен (Ip) – это индекс качественного показателя.
|
|
|
Индекс цен определяется по следующей формуле:
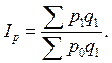(8.5)
Немецкие ученые Г. Пааше и Э. Ласпейрес предложили разные формулы для этих индексов в зависимости от используемых соизмерителей.
Для индексов Пааше соизмерителями являются параметры текущего периода, для индексов Ласпейреса – параметры базисного периода.
Пример 8.1
Рассмотрим применение индексного метода для изучения динамики сложных статистических совокупностей по данным табл. 8.1 о ценах и реализации товаров за два периода.
Таблица 8.1
| Товар | Единица измерения | I период | II период | Индивидуальные индексы | |||
| Цена за ед. измерения, руб. (р0) | Количество (q0) | Цена за ед. измерения, руб. (р1) | Количество (q1) | Цен
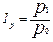
| Физического объема
| ||
| А | т | 1,25 | 1,27 | ||||
| Б | м | 1,0 | 1,25 | ||||
| В | шт. | 0,67 | 1,5 |
При определении по данным табл. 8.1 статистических индексов первый период принимается за базисный, в котором цена единицы товара обозначается р0, а количество – q0.
Второй период принимается за текущий (или отчетный), в котором цена единицы товара обозначается р1, а количество – q1.
Индивидуальные (однотоварные) индексы показывают, что в текущем периоде по сравнению с базисным цена на товар А повысилась на 25%, на товар Б – осталась без изменений, а на товар В – снизилась на 33%. Количество реализации товара А возросло на 27%, товара Б – на 25%, а товара В – на 50%.
Применим формулу Пааше для расчета агрегатного индекса цен по данным табл. 8.1:
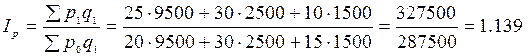, или 113,9%,
т.е. по данному ассортименту товаров в целом цены повысились в среднем на 13,9%.
Разность числителя и знаменателя индекса цен показывает абсолютный прирост товарооборота за счет изменения цен:
руб.
Следовательно, повышение цен на 13,9% обусловило увеличение объема товарооборота в текущем периоде на 40000 рублей. Величина этого показателя с противоположным знаком (–40000 рублей) характеризует перерасход денежных средств населением при покупке товаров по повышенным ценам.
Для определения индекса физического объема товарооборота применим формулу Ласпейреса
(8.6)
Поскольку в числителе формулы (8.8) содержится сумма стоимости реализации товаров в текущем периоде по неизменным (базисным) ценам, а в знаменателе – сумма фактической стоимости товаров, реализованных в базисном периоде в тех же неизменных (базисных) ценах, то данный индекс является агрегатным индексом товарооборота в сопоставимых (базисных) ценах.
Используем формулу (8.6) для расчета агрегатного индекса физического объема реализации товаров по данным табл. 8.1:
числитель индексного отношения
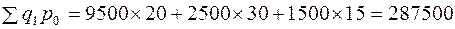руб.:
знаменатель индексного отношения
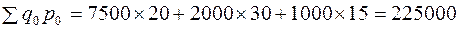руб.
Подставляя полученные суммы в формулу (8.6), получаем
или 127,8%,
т.е. по данному ассортименту товаров в целом прирост физического объема реализации в текущем периоде составил в среднем 27,8 %.
Вычитая из числителя знаменатель индексного отношения (8.6), получаем показатель, характеризующий прирост суммы товарооборота в текущем периоде по сравнению с базисным периодом в сопоставимых базисных ценах:
(8.7)
Применяя формулу (7.7) к данным табл. 8.1, вычислим сумму прироста товарооборота:
руб.,
т.е. в результате изменения физического объема реализации товара в текущем периоде получен прирост объема товарооборота в сопоставимых ценах на 62,5 тыс. руб.
Сопоставление значений 
и 
дает общий индекс товарооборота в текущих ценах
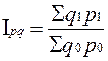, (8.8)
где – сумма фактического товарооборота текущего периода;
– сумма фактического товарооборота базисного периода.
Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным.
Величина объема товарооборота равняется произведению количества продажи товаров на цены. Следовательно, индекс физического объема Iq, умноженный на индекс цен Ip, дает индекс товарооборота в фактических ценах Ipq:
Ipq= Ip×Iq. (8.9)
Наличие связи между этими индексами (8.9) дает возможность по известным двум находить третий индекс.
Пример 8.2
Если в отчетном периоде товарооборот в фактических ценах возрос по сравнению с базисным периодом на 12%, а цены на реализованные товары снижены в среднем на 3%, то на основе этой информации можно определить изменение товарооборота в неизменных ценах:
. (8.10)
На основе исходной информации имеем: Iqp =1,12; Ip =0,97. Подставляя эти данные в формулу (8.10), определим индекс физического объема продажи товаров: Iq =1,12:0,97=1,154, или 115,4%, т.е. товарооборот в сопоставимых ценах увеличится в текущем периоде на 15,4%.
Из формулы (8.9) можно по известным индексам товарооборота в фактических ценах Iqp и товарооборота в сопоставимых ценах Iq определить индекс цен Ip:
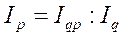. (8.11)
Так, если в отчетном периоде товарооборот в фактических ценах возрос на 7%, а физический объем реализованной товарной массы увеличен на 10%, то для определения по этим данным изменения цен используется формула (8.11): Ip =1,07:1,1=0,97, т.е. цены в отчетном периоде снизились на 3%.
Другие индексы также тесно связаны меду собой. Так, индекс издержек производства – это произведение индекса себестоимости продукции на индекс физического объема продукции:
, (8.12)
или 
(8.13)
Пример 8.3
Если себестоимость увеличилась на 10%, а количество продукции снизилось на 8%, то индекс издержек производства будет равен величине
1,10 × 0,92 = 1,012, или 101,2%.
В статистике применяется и другая форма индексов – средневзвешенные индексы. Их используют тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс.
Средний индекс –это индекс, исчисленный как средняя величина из индивидуальных индексов.
Средний арифметический индекс физического объема продукции вычисляется по формуле
(8.14)
Весами в этой формуле является стоимость продукции базисного периода. Средний гармонический индекс цен определяется выражением
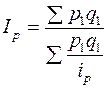. (8.15)
Здесь соизмерителем является стоимость продукции текущего периода.
В практике часто приходится определять изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов: изменением значения индексируемого показателя у отдельных групп единиц и изменением структуры явления. Так как на изменение среднего значения показателя оказывают воздействие два фактора, возникает задача определения степени влияния каждого из факторов на общую динамику средней.
Эта задача решается путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов.
Под изменением структуры явления понимается изменение доли отдельных групп единиц совокупности в общей их численности.
Индекс переменного состава –индекс, выражающий отношение средних уровней изучаемого явления, относящихся к разным периодам, и показывает изменение цен с учетом количества проданной продукции.
Индекс постоянного (фиксированного) состава –индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины.
Индекс структурных сдвигов –индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления (цен).
Индекс цен фиксированного (постоянного) состава рассчитывается по формуле
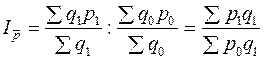. (8.16)
Индекс цен переменного состава:
. (8.17)
Индекс структурных сдвигов:
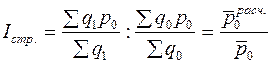. (8.18)
Система взаимосвязи индексов при анализе динамики средней цены имеет следующий вид:
(8.19)
Здесь
– средняя цена единицы объема в базисном периоде;
– средняя цена единицы объема в отчетном периоде;
– расчетная средняя цена продажи единицы объема в текущем периоде по ценам базисного периода.
Пример 8.4
Определить изменения цен и структуру продаж товаров табл. 8.2.
Таблица 8.2
Продажа товара в магазинах торговой ассоциации
| Магазин | Базисный период | Текущий период | Расчетные графы | ||||
| Удельный вес реализации, % | |||||||
| Цена 1 кг, руб. p0 | Кол-во, кг q0 | Цена 1 кг, руб. p1 | Кол-во, кг q1 | ip | Базисный | Отчетный | |
| 0,96 | 20,0 | 40,0 | |||||
| 0,97 | 40,0 | 30,0 | |||||
| 0,95 | 40,0 | 30,0 | |||||
| Σ |
При анализе изменений лишь уровней цен (гр. 2 и 4) исчисленные индексы ip (гр. 6) показывают, что в текущем периоде имело место снижение цен: в магазине №1 – на 4% (100-96%), в магазине №2 – на 3% (100-97%) и в магазине №3 – на 5% (100-95%).
Однако рассчитаны эти индексы безотносительно к объемам реализации.
Для определения изменения цен с учетом количества реализуемой продукции исчисляется индекс цен переменного состава
;
;
;
.
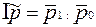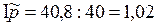Таким образом, средняя цена реализации данного продукта в трех магазинах в целом возросла в текущем периоде на 2%. Рост цен равен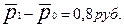 
Население при покупке каждого килограмма данного продукта переплачивало по 0,8 рублей (40,8 – 40,0). За счет действия каких факторов произошло это повышение? Для ответа на этот вопрос надо рассмотреть данные о структуре реализации товара по отдельным магазинам. Вычисленные в гр. 7 и 8 удельные веса реализации показывают: с 20% до 40% возрос удельный вес продажи в первом магазине (более дорогом); а удельные веса продажи в магазинах 2 и 3 снизились. Как это повлияло на среднюю цену? Определим индекс влияния структурных сдвигов на изменение средней цены (за счет перераспределения массы проданных товаров).
|
|
|
