 |
Взаимодействие между точечной массой и однородным шаром.
|
|
|
|
Точка массы 
находится на расстоянии 
от центра однородного шара радиуса 
и массы 
за его пределами. Силу взаимодействия можно определить, пользуясь предыдущими результатами. Для этого выделим в шаре сферический слой радиуса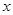 
и толщины 
с центром в центре шара. Масса выделенного слоя равна:
По (231) сила взаимодействия точки с выделенным слоем равна:
Интегрируя, получаем силу взаимодействия точки с шаром:
(232)
Если же точка находится внутри шара, надо учитывать взаимодействие только со слоями шара, с внутренними по отношению к точке:
(233)
где: 
- суммарная масса внутренних слоев шара, равная:
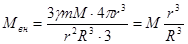
Отсюда сила взаимодействия равна:
(234)
Работа и энергия.
Работа силы, работа суммы сил.
Работой силы называют величину, равную произведение силы на перемещение точки приложения силы:
(235)
Как видно, если сила и перемещение взаимно перпендикулярны, работа силы равна нулю. Например, центростремительная сила не производит работы, ее роль сводится лишь к искривлению траектории.
Работа суммы сил равна сумме работ, производимых отдельными силами системы. Например:
(236)
Частные случаи вычисления работы.
Работа силы тяжести.
Рис.54
Пусть тело под действием силы тяжести скользит по наклонной поверхности произвольной формы (рис.54.) работа нормальной реакции по (235) равна нулю, поэтому при отсутствии трения работу совершает только сила тяжести. На элементарном перемещении работа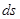 
силы равна:
(237)
Следовательно, на конечном перемещении работа сил тяжести не зависит от формы траектории и равна:
где: 
перемещение тела по вертикали.
Работа упругих сил.
На гладкой горизонтальной плоскости находится тело, скрепленное пружиной жесткости 
с вертикальной стенкой (рис.55).
|
|
|
Рис.55
Если под действие внешней силы 
пружина растягивается на 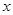, возникает сила упругости пружины, равная в пределах упругих деформаций 
. Элементарная работа упругих сил по перемещению тела из этого положения на равна:
Работа же силы на конечном перемещении:
(238)
где 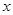– растяжение (удлинение) пружины.
Работа и кинетическая энергия.
Если на тело массы m действует постоянная сила , работа ее на перемещении 
:
т.е. равна разности кинетических энергий тела в конце и в начале перемещения.
Аналогичный результат можно получить и для переменной силы. Для этого разобьем все перемещение на малые участки, в пределах которых силу можно считать постоянной и ее работу вычислить по (239):
,
,
На всем перемещении работа силы равна:
(240)
Если же на тело действуют дополнительно силы трения, получаем:
(241)
где: 
и 
- скорость тела в конце и в начале перемещения, А 
- работа сил трения.
Следовательно, работа силы равна:
(242)
Работа центральных сил.
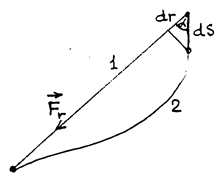
Рис.56
Если на тело действует центральная сила (рис.56), ее работа на элементарном перемещении 
вдоль линии действия силы равна (вдоль траектории1):
(243)
а работа на конечном перемещении:
(244)
При движении по произвольной траектории на элементарном перемещении работа силы выражается соотношением:
т.е. совпадает с (243). Т.е. работа центральных сил не зависит от формы траектории, а определяется лишь начальным и конечным положениями перемещаемого тела.
Силы, работа которых не зависит от формы траектории, называют консервативными. К ним, например, относятся силы упругости, силы электростатического взаимодействия между точечными зарядами, гравитационные силы, а силы трения – не являются консервативными.
Потенциальная энергия.
Потенциальной энергией называют энергию, определяемую конфигурацией системы, относительным расположением отдельных взаимодействующих тел. выражение для потенциальной энергии для произвольного взаимодействия записать сложно, обычно определяют ее изменение относительно уровня, условно принятого за нулевой. например, потенциальная энергия тела массы m в поле тяготения Земли, находящегося на высоте h над ее поверхностью:
|
|
|
а на поверхности:
Изменение потенциальной энергии тела относительно поверхности Земли:
(225)
При « (225) принимает вид:
Таким выражением и пользуются, как правило, при расчетах. Здесь потенциальная энергия отсчитывается от определенного уровня (поверхности Земли), на которое она условно принята нулевой.
Такой подход оправдан тем, что при изменениях конфигурации систем изменение состояния определяется не самим значением потенциальной энергии, а только изменением ее.
|
|
|
