Скорость отдельных точек тела при плоском движении.

 

Выберем в качестве полюса т. А (рис. 16) и выделим произвольную точ­ку B сечения тела. Положение их в пространстве определим векторным способом (r_a и r_b соответственно). Кроме того, положение т. В определим, указав радиус-вектор r.

 

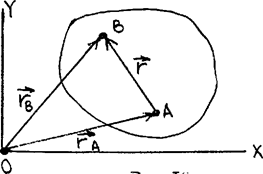рис 16

По определений скорость т. В:

 

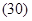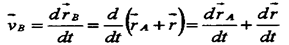Таким образом, скорость любой точки тела при плоском движении определяется суммой двух составляющих. Выясним их смысл.

Если в процессе движения тела (движение поступательное) то:

 

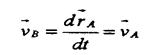Следовательно, эта составляющая определяет скорость поступательной части движения вместе с

полюсом. Если же в процессе дви­жения (вращение вокруг т. А), скорость точки В равна:

 

 

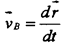очевидно, что эта составляющая представляет собой линейную скорость вращательной части движения вокруг полюса.

Таким образом, в любой момент времени скорость произвольной точки тела, совершающего плоское движение, определяется векторной суммой скоростей поступательного движения вместе с полюсом и вра­щательного движения вокруг полюса.

Может оказаться так, что для какой-либо точки тела сумма окажется равной нулю (точка в данный момент времени покоится). Такую точку называют мгновенным центром вращения, и плоское дви­жение тела можно рассматривать в данный момент времени как вращение вокруг мгновенного центра вращения. Примером мгновенного центра может служить точка касания цилиндра с плоскостью, по ко­торой он катится без скольжения.

Задачи кинематики.

ПЕРВАЯ ЗАДАЧА КИНЕМАТИКИ.

 

Первая задача кинематики состоит в нахождении кинематических характеристик движения по заданному закону движения.

Пример: Закон движения точки задан в координатной форме

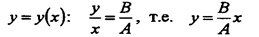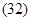Прежде всего, определим уравнение траектории точки в виде

 

 

Следовательно, траекторией точки является прямая (рис. 17).

(рис. 17)

Прямая ограничена максимальными отклонениями точ­ки от положения равновесия ±А вдоль оси ОХ и ±B вдоль ОY.

 

 

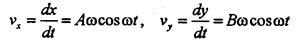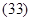Составляющие скорости равны:

 

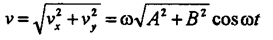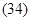а полная скорость:

 

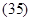Ускорение точки в проекциях на координатные оси:

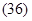а полное:

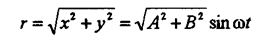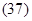Таким образом, точка совершает гармонические колебания вдоль прямой, при этом ее скорость и ускорение изменяются тоже по гармоническому закону. Отклонение точки от положения равновесия:

 

ВТОРАЯ (ОСНОВНАЯ) ЗАДАЧА КИНЕМАТИКИ

Вторая задача состоит в нахождении закона движения и кинематических характеристик движения по заданному ускорению и на­чальным условиям. Под начальными условиями понимают значения координат и скорости точки в начальный момент времени t=t₀=0,

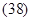Пусть ускорение точки задано его составляющими:

 

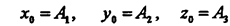Начальные условия:

 

 

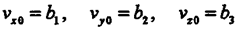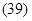Рассмотрим сначала движение точки вдоль оси координат OX. По условию:

 

 

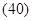откуда:

 

 

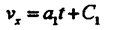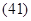Интегрируя (40), получаем:

 

Постоянную интегрирования C1 определяем из начальных условий:

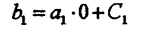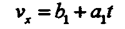
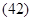т.е.:

 

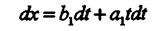
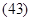Из (42) следует, что

 

 

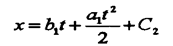Интегрируя (43), получаем:

 

Постоянную интегрирования С₂ также получаем из начальных

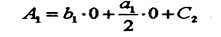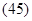условий:

 

следовательно:

 

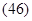
Аналогично получаем для других координатных направлений:

 

 

 

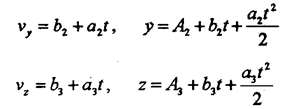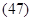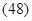Полная скорость равна:

 

 

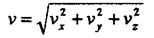
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ.

Сила.

ОПРЕДЕЛЕНИЯ:

Изменение состояния тела происходит в результате взаимодей­ствий, которые приводят к изменению, как внутреннего состояния тел, так и состояния их движения. Количественной мерой взаимо­действий, приводящих к изменению состояний тел, является сила.

Сила - векторная величина, она характеризуется следующими элементами: величиной, направлением в пространстве и точкой при­ложения силы.

Линия, вдоль которой направлена сила, называется линией действия силы.

Совокупность сил, приложенных к телу, называют системой сил.

 

Если под действием системы сил, приложенных к телу, оно может пребывать в состоянии покоя, система называется уравновешенной

Если одну систему сил, приложенных к телу, можно заменить другой, не изменяя его состояние, системы называются эквивалентными.

Сила, эквивалентная системе сил, называется равнодействующей этой системы.

Сила, равная по величине равнодействующей и противоположно ей направленная, называется уравновешивающей.

Силы взаимодействия между телами одной и той же системы называются внутренними.

Силы взаимодействия с телами, не входящими в состав данной системы называются внешними.

Силы, приложенные в одной точке тела, называются сосредото­ченными.

Силы, приложенные ко всем точкам поверхности или объема тела, называются распределенными.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: