 |
Галилеевы преобразования координат и закон сложения скоростей.
|
|
|
|
Предположим, что одна из систем отсчета неподвижна, а другая - движется относительно первой с постоянной скоростью, так что оси ОХ,O’Х' и OY,0'Y' остается параллельными, а ось 0'Y' скользит вдоль OY со скоростью (рис.30).
 | |||
 |
Положение т. А можно задать векторным и координатным способами в обеих системах отсчета. Будем считать, что в исходный момент времени системы полностью совпадают. Тогда к моменту времени t, измеренному в неподвижной системе, подвижная система совершит перемещение. Координаты т. А в двух системах отсчета связаны соотношениями:
х' = х (133)
(134)
z'=z (135)
Опыт показывает, что течение времени в обеих системах одинаково:
t'=t (136)
Совокупность соотношений (133, 134, 135, 136) и представляет собой преобразования Галилея в координатной форме.
Более компактную форму принимают преобразования Галилея, если положение т. А определять векторным способом:
 |  | ||
t' = t (138)
Справедливы и преобразования Галилея для обратного перехода:
х = х ' (139)
(140)
z=z' (141)
t=t’ (142) или
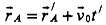(143)
t = t' (144)
Скорость т. А в двух системах отсчета связана соотношением:
 |
Принцип относительности Галилея, его физический смысл.
Из закона сложения скоростей Галилея (145) следует, что ускорение тела в двух инерциальных системах отсчета, находящихся в относительном движении, одинаковы:
(146)
Механические опьггы, так или иначе, связаны со 2-м законом Ньютона, т.е. с определением ускорения тела. Результат опыта (измеряемое ускорение) оказывается одинаковым во всех инерциальных системах отсчета. Это дает основание сформулировать механический принцип относительности (принцип относительности Галилея): никакими механическими опытами, проводимыми внутри инициальной системы, нельзя отличить ее от другой инерциальной системы.
|
|
|
При таком утверждении предполагается, что 2-й закон Ньютона имеет одинаковую форму в различных инфернальных системах, что очевидно. Закон будет иметь одинаковую форму в том случае, если отдельные физические величины, входящие в него, не преобразуются при переходе от одной инерциальной системы отсчета к другой:
F’ = F, m’ = m, a’ = a
Из закона сложения скоростей Галилея следует, что а' = а. Опыт показывает, что при небольших скоростях по сравнению со скоростью света масса тела также одинакова во всех инерциальных системах.
Что касается сил, то их основные типы зависят от времени, относительного расстояния между взаимодействующими телами и относительной скорости тел. Если эти параметры одинаковы в разных системах отсчета, то одинаковы и силы. Равенство параметров следует из преобразований Галилея и закона сложения скоростей. Поэтому механический принцип относительности можно сформулировать и таким образом. Законы динамики ковариантны по отношению к преобразованиям Галилея.
Основы специальной теории относительности.
Постулаты Эйнштейна.
В основе специальной теории относительности, прежде всего, лежит факт постоянства скорости света в различных системах отсчета, что противоречит классическому закону сложения скоростей. Кроме того, нет никаких оснований считать, что механические опьггы позволят отличить одну инициальную систему отсчета от другой. Это позволило Эйнштейну сформулировать исходные постулаты специальной теории относительности.
Постулат о постоянстве скорости света: скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источника и приемника света.
Постулат относительности (общефизический принцип относительности): Никакими физическими опытами нельзя отличить одну инерциальную систему отсчета от другой. Наряду с этими постулатами Эйнштейн ввел принцип синхронизации часов, имеющий такое же значение в теории относительности, как и сформулированные выше постулаты.
|
|
|
Для того, чтобы одинаковые по устройству часы А и В (рис.31)
 |
шли одинаково, необходимо их синхронизировать. Пусть в момент времени, отсчитанный по часам А, в том месте, где они находятся, осуществляется световая вспышка. Сигнал от нее достигает часов В, мгновенно отражается и поступает к часам А в момент времени, отсчитанный по ним. Часы А и В считаются синхронизированными, если в момент отражения сигнала в т. В показания часов равны:
По сути дела в принципе синхронизации постулируется утверждение, что прямой и отраженный сигналы движутся с одинаковой скоростью, а само отражение происходит мгновенно, что не следует из сформулированных ранее постулатов.
Исходя из указанных постулатов, можно получить все основные выводы специальной теории относительности.
8.2. "Радиолокационный" метод (метод коэффициента "k ").
Движение тел можно графически представлять диаграммами x=x(t). В случае скоростей, сравнимых со скоростью света, масштаб х и t выбирается таким, что траектория светового сигнала ("световая линия") делит координатный угол пополам. Если же тело движется со скоростью, меньшей скорости света, угол наклона его траектории к оси t меньше 45°.
Предположим, что две инерциальные системы отсчета А и В находятся в относительном движении. Систему А условно считаем неподвижной. В исходный момент времени системы полностью совпадали. В этот момент осуществляется синхронизация подвижных и неподвижных часов и на них устанавливаются нулевые показания. Далее система В удаляется от А со скоростью v<c (рис.32).
Рис.32
Затем в системе А производится вторая вспышка в момент времени t, измеренный по часам А. Сигнал от нее догоняет систему В в момент времени, измеренный по часам В в подвижной системе, а показания неподвижных часов А для этого события равны. Сигнал мгновенно отражается и приходит в систему А в момент времени, отсчитанный по часам А.
|
|
|
Предположим, что показания подвижных часов в момент отражения сигнала в k раз отличаются от показаний неподвижных часов t в момент посылки сигнала:
= kt (148)
Системы равноправны, поэтому с момента отражения неподвижной можно считать систему В, а систему А - подвижной. Тогда показания часов А в момент приема сигнала равны:
(150)
С момента синхронизации до отражения сигнала система В и световой сигнал, посланный в момент времени t (по часам А), проходят одинаковый путь:
т.е.
откуда получаем значение коэффициента k:
 | |||
 | |||
Следовательно, показания подвижных часов в момент приема сигнала всегда больше показаний неподвижных часов в момент посылки сигнала:
 |
8.3. "Замедление" хода времени.
Рассмотрим на описанном выше примере промежуток времени между двумя событиями (синхронизация часов и отражение сигнала), измеренный по часам А и В. Поскольку в момент синхронизации показания обоих часов нулевые, то промежуток времени численно равен показаниям часов в момент отражения сигнала. Обозначив промежуток времени, измеренный по часам А и В, соответственно и, отношение этих показаний запишем в виде:
 |
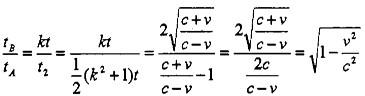откуда:
(152)
Следовательно, промежуток времени между двумя событиями, измеренный подвижными часами, меньше результата того же измерения по неподвижным часам.
Относительная скорость.
Предположим, что системы А, В и D находятся в относительном движении. В исходный момент все три системы совпадали. В этот момент производим синхронизацию всех часов и устанавливаем на них нулевые показания. Далее система В удаляется от А со скоростью v1, а система D - со скоростью v2 >v1. В момент времени t (пo часам А) в системе А производится световая вспышка, сигнал от которой достигает (рис.33)
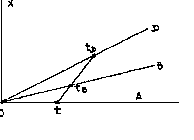
Рис.33
системы В в момент tB =k1t (по часам В) и системы D в момент tD = k2t (по часам D ). При этом:
 | |||
 | |||
Теперь будем считать систему В неподвижной, а систему D - удаляющейся от B с относительной скоростью и. Тогда:
|
|
|
(154)
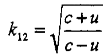где:
Следовательно:
 |
откуда:
Это и есть выражение для относительной скорости.
|
|
|
