Главная | Обратная связь | Поможем написать вашу работу!

Нормировка потенциальной энергии, закон сохранения энергии.

Положим, что в замкнутой консервативной системе выделены состояния 1, 2 и 3, условно принятое за исходное, При переходе из состояний 1, 2 в исходное (рис. 57) работа консервативных сил равна:

(рис. 57)

(246)

(247)

откуда:

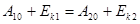(248)

Т.е. для любых состояний системы кинетическая энергия в этом состоянии и работа внутренних сил по переходу из выбранного состояния в исходное - величина постоянная для всех состояний системы. При этом знак работы определяется выбором исходного состояния. Для расчетов важно, чтобы работа сил на любом переходе имела одинаковый знак, поэтому в выражении (248) к значению работы надо добавить такую положительную величину 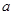, чтобы:

Сама проделанная операция выбора 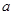называется нормировкой потенциальной энергии, а сумма - потенциальной энергией системы в данном состоянии. С учетом сказанного:

(249)

для всех состояний системы. Это и есть закон сохранения механической энергии.

Пример нормировки приведен в предыдущем параграфе.

14. Динамика твёрдого тела.

Абсолютно твердым телом называют абсолютно неизменяемую систему точек, отдельных частиц тела, поэтому к абсолютно твердому телу можно применить уже описанные законы динамики системы точек при условии ее неизменяемости.

Момент инерции твёрдого тела.

Для описания вращательного движения тела существенно значение его момента инерции. По определению момент инерции твердого тела равен сумме моментов инерции отдельных его частиц:

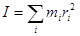
где 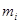- масса -й частицы тела, - ее расстояние от заданного центра или оси.

Предположим, что масса выделенной частицы тела 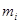, расстояние от нее до начала координат (т. о) , а координаты, соответственно, (рис. 58).

Момент инерции относительно т. О по определению равен

(250)

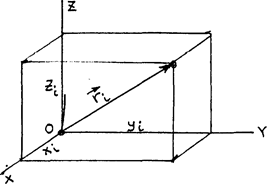
(рис. 58)

а относительно координатных осей:

(251)

(252)

(253)

Сравнивая (230), (231), (232) и (233), получим связь момента инерции тела относительно начала координат с моментами инерции относительно координатных осей:

(254)

Если одним из размеров тела можно пренебречь по сравнению с двумя другими (плоское тело), эта связь запишется в виде

(255)

Примеры расчёта сил инерции.

Момент инерции тонкого стержня относительно оси, перпендикулярной стержню и проходящий через его центр масс.

(рис. 59)

Если стержень имеет массу и длину , а ось проходит через центр масс стержня (рис. 59), то координаты левого и правого концов стержня равны - 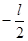и . Выделим в стержне на расстоянии 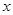от оси малый его участок длины . Его момент инерции относительно равен:

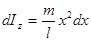(256)

Интегрируя (236), получим:

(257)

Момент инерции тонкой пластины прямоугольной формы относительно одной из её сторон.

(рис. 60)

Размеры тонкой пластины массы приведены на рис. 60, выделим в пластине на расстоянии 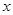от оси узкий слой ширины и запишем его момент инерции:

(258)

Интегрируя (258), получаем:

(259)

Момент инерции однородного шара относительно его центра.

Пусть масса шара равна , а радиус . Выделим в шаре тонкий сферический слой радиуса 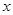, толщины , момент инерции которого относительно центра шара равен

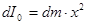(260)

где:

Интегрируя (260), получим искомый результат:

(261)

Теорема Штейнера.

Расчет моментов инерции тела даже правильной формы, если ось не проходит через центр масс тела, затруднен. В этом случае удобно пользоваться теоремой Штейнера:

Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси , параллельной заданной и проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями:

Для доказательства через центр масс тела (т. С) проведем ось , параллельную заданной оси (рис. 61). Расстояние между осями равно 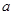. Выберем частицу тела массы 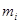, настояние от нее до осей и указаны на рисунке.