Сравнение поперечных размеров тел.

 

Пусть две системы OXYZ и O'X'Y'Z' находятся в относительном движении. Одну из них, OXYZ, считаем неподвижной, другая же движется со скоростью v относительно первой так, что оси ОХ, 0'Х' и 0Z, О’Z' остаются параллельными, а ось О’Y' скользит вдоль оси OY. В подвижной системе вдоль оси O'Z' расположены "световые часы" (жесткий стержень с двумя зеркалами на концах, отражающими поверхностями друг к другу) так, что нижнее зеркало совпадает с началом системы отсчета (рис.34). В исходный момент, когда системы полностью совпадали, у нижнего зеркала произошла световая вспышка. Сигнал от нее достигает верхнего зеркала, отражается, приходит опять к нижнему зеркалу, и далее процесс повторяется периодически. Пусть по неподвижным часам промежуток

 

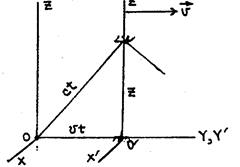Рис.34

времени между вспышкой и приходом сигнала равен t. За это время в неподвижной системе световой сигнал проходит путь сt, а подвижная система - vt. Из рисунка видно, что длина световых часов, численно равная координате z верхнего зеркала, в неподвижной системе равна:

(157)

В подвижной системе, связанной с подвижными часами, длина их равна:

z'=ct' (158)

где: t ' - полупериод часов, т.е. промежуток времени между вспышкой и приходом сигнала к верхнему зеркалу.

Учитывая эффект "замедления" хода времени, получаем:

 

т.е. поперечные размеры (по отношению к направлению движения) тел одинаковы в обеих системах отсчета:

z'=z

8.6. Эффект "сокращения" длин.

 

 

Пусть теперь световые часы ориентированы вдоль оси подвижной системы так, что левое зеркало совпадает с ее началом. В исходный момент системы совпадали, и в этот момент у левого зеркала произошла вспышка. Сигнал от нее достигает правого зеркала через промежуток

времени t₁ по неподвижным часам (рис.35). Тогда:

 

где: l - длина световых часов, измеренная в неподвижной системе.

После отражения сигнал и левое зеркало движутся навстречу друг другу и встречаются в момент времени t₂ по неподвижным часам. Очевидно, что:

 

 

Период световых часов, измеренный в неподвижной системе, равен:

 

В подвижной системе период часов определяется соотношением:

(163)

 

где l' - длина часов, измеренная в подвижной системе. Отсюда:

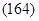т.е.:

 

 

 

Следовательно, продольные размеры тел в любой системе меньше собственных:

Преобразования Лоренца.

Преобразования Лоренца дают связь между пространственными и временными координатами событий в двух инициальных системах отсчета, находящихся в относительном движении.

Учитывая, что поперечные размеры тел одинаковы, получаем:

z'=z (166)

х'=x (167)

Для сравнения координат у обратимся к предыдущему примеру:

 

 

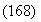С другой стороны, это соотношение можно представить в виде:

 

т.е.

 

Соотношения (166,167,168,170) называют преобразованиями Лоренца.

8.8. Интервал. Инвариантность интервала.

Интервалом S между двумя событиями называют величину, квадрат которой равен:

 

где x_i,y_i,z_i,t_i - пространственные и временные координаты событий.

Используя преобразования Лоренца, запишем интервал в подвижной системе отсчета:

 

 

Таким образом, интервал является инвариантом:

S ^/2=S ² (171)

 

В зависимости от соотношения между временной cΔt и -

пространственной частями интервала различают:

1.Времениподобные интервалы (cΔt > Δl).

2.Пространственноподобные интервалы (cΔt <s Δl).

3. Светоподобные интервалы (сΔt = Δl).

Преобразования компонентов вектора скорости.

Преобразования компонентов вектора скорости можно получить, пользуясь преобразованиями Лоренца:

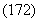⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: